- Runcinated 120-cell
-
Four runcinations 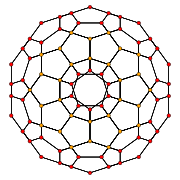
120-cell







Runcinated 120-cell
(Expanded 120-cell)








Runcitruncated 120-cell







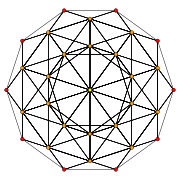
600-cell







Runcitruncated 600-cell
(Expanded 600-cell)







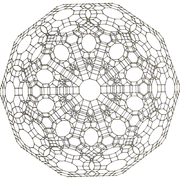
Omnitruncated 120-cell







Orthogonal projections in H3 Coxeter plane In four-dimensional geometry, a runcinated 120-cell (or runcinated 600-cell) is a convex uniform polychoron, being a runcination (a 3rd order truncation) of the regular 120-cell.
There are 4 degrees of runcinations of the 120-cell including with permutations truncations and cantellations.
The runcinated 120-cell can be seen as an expansion applied to a regular polychoron, the 120-cell or 600-cell.
Contents
Runcinated 120-cell
Runcinated 120-cell Type Uniform polychoron Uniform index 38 Coxeter-Dynkin diagram 






Cells 2640 total:
120 5.5.5
720 4.4.5
1200 4.4.3
600 3.3.3
Faces 7440:
2400{3}+3600{4}+
1440{5}Edges 7200 Vertices 2400 Vertex figure 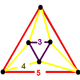
Equilateral-triangular antipodiumSchläfli symbol t0,3{5,3,3} Symmetry group H4, [3,3,5] Properties convex The runcinated 120-cell is a uniform polychoron. It has 2640 cells: 120 dodecahedra, 720 pentagonal prisms, 1200 triangular prisms, and 600 tetrahedra. Its vertex figure is a nonuniform triangular antiprism (equilateral-triangular antipodium): its bases represent a dodecahedron and a tetrahedron, and its flanks represent three triangular prisms and three pentagonal prisms.
Alternate names
- Runcinated 120-cell / Runcinated 600-cell (Norman W. Johnson)
- Runcinated hecatonicosachoron / Runcinated hexacosichoron / Runcinated polydodecahedron / Runcinated polytetrahedron
- Small diprismatohexacosihecatonicosachoron (acronym: sidpixhi) (George Olshevsky, Jonathan Bowers)[1]
Images

Schlegel diagram (Only tetrahedral cells shown) 
H3
A2/B3Orthogonal projections in Coxeter planes Runcitruncated 120-cell
Runcitruncated 120-cell Type Uniform polychoron Uniform index 43 Coxeter-Dynkin diagram 






Cells 2640 total:
120 (3.10.10)
Faces 13440:
4800{3}+7200{4}+
1440{10}Edges 18000 Vertices 7200 Vertex figure 
Irregular rectangular pyramidSchläfli symbol t0,1,3{5,3,3} Symmetry group H4, [3,3,5] Properties convex The runciruncated 120-cell is a uniform polychoron. It contains 2640 cells: 120 truncated dodecahedra, 720 decagonal prisms, 1200 triangular prisms, and 600 cuboctahedra. Its vertex figure is an irregular rectangular pyramid, with one truncated dodecahedron, two decagonal prisms, one triangular prism, and one cuboctahedron.
Alternate names
- Runcicantellated 600-cell (Norman W. Johnson)
- Prismatorhombated hexacosichoron (Acronym: prix) (George Olshevsky, Jonathan Bowers)[2]
Images

Schlegel diagram (Only triangular prisms shown) 
H3
A2/B3Orthogonal projections in Coxeter planes Runcitruncated 600-cell
Runcitruncated 600-cell Type Uniform polychoron Uniform index 44 Coxeter-Dynkin diagram 






Cells 2640 total:
120 3.4.5.4
720 4.4.5
1200 4.4.6
600 3.6.6
Faces 13440:
2400{3}+7200{4}+
1440{5}+2400{6}Edges 18000 Vertices 7200 Vertex figure 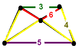
Trapezoidal pyramidSchläfli symbol t0,1,3{3,3,5} Symmetry group H4, [3,3,5] Properties convex The runcitruncated 600-cell is a uniform polychoron. It is composed of 2640 cells: 120 rhombicosidodecahedron, 600 truncated tetrahedra, 720 pentagonal prisms, and 1200 hexagonal prisms. It has 7200 vertices, 18000 edges, and 13440 faces (2400 triangles, 7200 squares, and 2400 hexagons).
Alternate names
- Runcicantellated 120-cell (Norman W. Johnson)
- Prismatorhombated hecatonicosachoron (Acronym: prahi) (George Olshevsky, Jonathan Bowers)[3]
Images

Schlegel diagram 
H3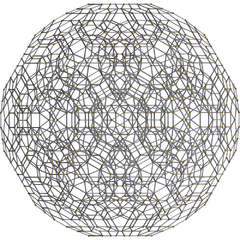
A2/B3Orthogonal projections in Coxeter planes Omnitruncated 120-cell
Omnitruncated 120-cell Type Uniform polychoron Uniform index 46 Coxeter-Dynkin diagram 






Cells 2640 total:
120 4.6.10
720 4.4.10
1200 4.4.6
600 4.6.6
Faces 17040 total:
10800 {4}, 4800 {6}
1440 {10}Edges 28800 Vertices 14400 Vertex figure 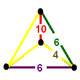
Chiral scalene tetrahedronSchläfli symbol t0,1,2,3{3,3,5} Symmetry group H4, [3,3,5] Properties convex The omnitruncated 120-cell is a convex uniform polychoron, composed of 2640 cells: 120 truncated icosidodecahedra, 600 truncated octahedra, 720 decagonal prisms, and 1200 hexagonal prisms. It has 14400 vertices, 28800 edges, and 17040 faces (10800 squares, 4800 hexagons, and 1440 decagons). It is the largest nonprismatic convex uniform polychoron.
The vertices and edges form the Cayley graph of the Coxeter group H4.
Alternate names
- Omnitruncated 120-cell / Omnitruncated 600-cell (Norman W. Johnson)
- Omnitruncated hecatonicosachoron / Omnitruncated hexacosichoron / Omnitruncated polydodecahedron / Omnitruncated polytetrahedron
- Great diprismatohexacosihecatonicosachoron (Acronym gidpixhi) (George Olshevsky, Jonathan Bowers)[4]
Images

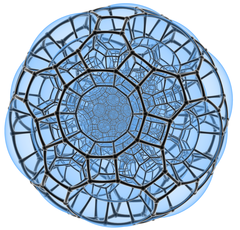
Schlegel diagram (centered on truncated icosidodecahedron)
(Orthogonal view, centered on decagonal prism cell.)Stereographic projection
(centered on truncated icosidodecahedron)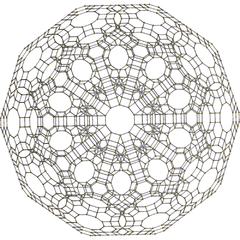
H3
A2/B3Orthogonal projections in Coxeter planes 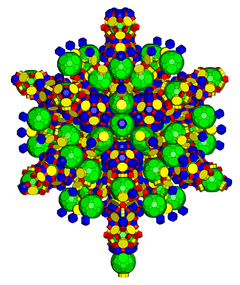
Polychoric netModels
The first complete physical model of a 3D projection of the omnitruncated 120-cell was built by a team led by Daniel Duddy and David Richter on August 9, 2006 using the (Zome) system in the London Knowledge Lab for the 2006 Bridges Conference.[5]
Related polytopes
These polytopes are a part of a set of 15 uniform polychorons with H4 symmetry:
H4 family polytopes by name, Coxeter-Dynkin diagram, and Schläfli symbol 120-cell rectified
120-celltruncated
120-cellcantellated
120-cellruncinated
120-cellbitruncated
120-cellcantitruncated
120-cellruncitruncated
120-cellomnitruncated
120-cell






























































{5,3,3} t1{5,3,3} t0,1{5,3,3} t0,2{5,3,3} t0,3{5,3,3} t1,2{5,3,3} t0,1,2{5,3,3} t0,1,3{5,3,3} t0,1,2,3{5,3,3} 






600-cell rectified
600-celltruncated
600-cellcantellated
600-cellruncinated
600-cellbitruncated
600-cellcantitruncated
600-cellruncitruncated
600-cellomnitruncated
600-cell






























































{3,3,5} t1{3,3,5} t0,1{3,3,5} t0,2{3,3,5} t0,3{3,3,5} t1,2{3,3,5} t0,1,2{3,3,5} t0,1,3{3,3,5} t0,1,2,3{3,3,5} Notes
References
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation [2] m55 m62 m60 m64
- Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 38, 44, 47, George Olshevsky.
- Richard Klitzing, 4D, uniform polytopes (polychora) x3o3o5x - sidpixhi, x3o3x5x - prix, x3x3o5x - prahi, x3x3x5x - gidpixhi
Fundamental convex regular and uniform polytopes in dimensions 2–10 Family An BCn Dn E6 / E7 / E8 / F4 / G2 Hn Regular polygon Triangle Square Hexagon Pentagon Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron Uniform polychoron 5-cell 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221 Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321 Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421 Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube n-polytopes n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 pentagonal polytope Topics: Polytope families • Regular polytope • List of regular polytopes Categories:- Four-dimensional geometry
- Polychora
- Runcinated 120-cell / Runcinated 600-cell (Norman W. Johnson)
Wikimedia Foundation. 2010.
