Root system

This article discusses root systems in mathematics. For root systems of plants, see root.

Lie groups
Classical groups General linear group GL(n) Special linear group SL(n) Orthogonal group O(n) Special orthogonal group SO(n) Unitary group U(n) Special unitary group SU(n) Symplectic group Sp(n)
Simple Lie groups List of simple Lie groups Infinite simple Lie groups: An, Bn, Cn, Dn, Exceptional simple Lie groups: G2 F4 E6 E7 E8
Other Lie groups Circle group Lorentz group Poincaré group Conformal group Diffeomorphism group Loop group
Lie algebras Exponential map Adjoint representation of a Lie group Adjoint representation of a Lie algebra Killing form Lie point symmetry
Structure of semi-simple Lie groups Dynkin diagrams Cartan subalgebra Root system Real form Complexification Split Lie algebra Compact Lie algebra
Representation theory Representation of a Lie group Representation of a Lie algebra
Lie groups in Physics Particle physics and representation theory Representation theory of the Lorentz group Representation theory of the Poincaré group Representation theory of the Galilean group
v · mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras. Since Lie groups (and some analogues such as algebraic groups) and Lie algebras have become important in many parts of mathematics during the twentieth century, the apparently special nature of root systems belies the number of areas in which they are applied. Further, the classification scheme for root systems, by Dynkin diagrams, occurs in parts of mathematics with no overt connection to Lie theory (such as singularity theory). Finally, root systems are important for their own sake, as in graph theory in the study of eigenvalues. Definitions 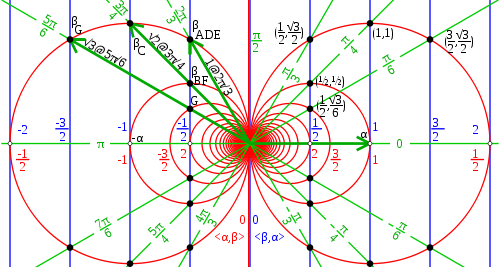The integrality condition for <β, α> is fulfilled only for β on one of the vertical lines, while the integrality condition for <α, β> is fulfilled only for β on one of the red circles. Any β perpendicular to α (on the Y axis) trivially fulfills both with 0, but does not define an irreducible root system. Modulo reflection, for a given α there are only 5 nontrivial possibilities for β, and 3 possible angles between α and β in a set of simple roots. Subscript letters correspond to the series of root systems for which the given β can serve as the first root and α as the second root. (or in F4 as the middle 2 roots) Let V be a finite-dimensional Euclidean vector space, with the standard Euclidean inner product denoted by $(\cdot,\cdot)$. A root system in V is a finite set Φ of non-zero vectors (called roots) that satisfy the following properties: The roots span V. The only scalar multiples of a root α ∈ Φ that belong to Φ are α itself and –α. For every root α ∈ Φ, the set Φ is closed under reflection through the hyperplane perpendicular to α. That is, for any two roots α and β, the set Φ contains the reflection of β, $\sigma_\alpha(\beta) =\beta-2\frac{(\alpha,\beta)}{(\alpha,\alpha)}\alpha \in \Phi.$ (Integrality condition) If α and β are roots in Φ, then the projection of β onto the line through α is a half-integral multiple of α. That is, $\langle \beta, \alpha \rangle = 2 \frac{(\alpha,\beta)}{(\alpha,\alpha)} \in \mathbb{Z}.$ Some authors only include conditions 1–3 in the definition of a root system. In this context, a root system that also satisfies the integrality condition is known as a crystallographic root system. Other authors omit condition 2; then they call root systems satisfying condition 2 reduced. In this article, all root systems are assumed to be reduced and crystallographic. In view of property 3, the integrality condition is equivalent to stating that β and its reflection σα(β) differ by an integer multiple of α. Note that the operator $\langle \cdot, \cdot \rangle \colon \Phi \times \Phi \to \mathbb{Z}$ defined by property 4 is not an inner product. It is not necessarily symmetric and is linear only in the first argument. The cosine of the angle between two roots is constrained to be a half-integral multiple of a square root of an integer: $\langle \beta, \alpha \rangle \langle \alpha, \beta \rangle = 2 \frac{(\alpha,\beta)}{(\alpha,\alpha)} \cdot 2 \frac{(\alpha,\beta)}{(\beta,\beta)} = 4 \frac{(\alpha,\beta)^2}{\vert \alpha \vert^2 \vert \beta \vert^2} = 4 \cos^2(\theta) = (2\cos(\theta))^2 \in \mathbb{Z}.$ Since $2\cos(\theta) \in [-2,2]$, the only possible values are $0, \pm \tfrac{1}{2}, \pm\tfrac{\sqrt{2}}{2}, \pm\tfrac{\sqrt{3}}{2}, \pm\tfrac{\sqrt{4}}{2} = 1$, corresponding to angles of 90°, 60° or 120°, 45° or 135°, 30° or 150°, and 0 or 180°. Condition 2 says that no scalar multiples of α other than 1 and -1 can be roots, so 0 or 180°, which would correspond to 2α or -2α are out. The rank of a root system Φ is the dimension of V. Two root systems may be combined by regarding the Euclidean spaces they span as mutually orthogonal subspaces of a common Euclidean space. A root system which does not arise from such a combination, such as the systems A2, B2, and G2 pictured below, is said to be irreducible. Two irreducible root systems (E1, Φ1) and (E2, Φ2) are considered to be the same if there is an invertible linear transformation E1 → E2 which sends Φ1 to Φ2. The group of isometries of V generated by reflections through hyperplanes associated to the roots of Φ is called the Weyl group of Φ. As it acts faithfully on the finite set Φ, the Weyl group is always finite. The root lattice of a root system Φ is the Z-submodule of V generated by Φ. It is a lattice in V. 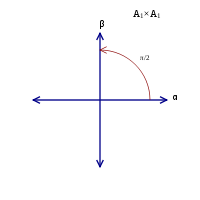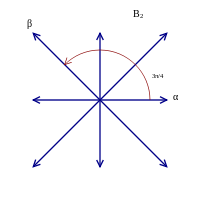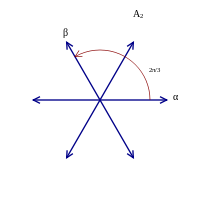Rank-1 and rank-2 examples Rank-2 root systems Root system $A_1 \times A_1$ Root system A2 Root system B2 Root system G2 There is only one root system of rank 1, consisting of two nonzero vectors {α, − α}. This root system is called A1. In rank 2 there are four possibilities, corresponding to σα(β) = β + nα, where n = 0,1,2,3. Note that the lattice generated by a root system is not unique: $A_1 \times A_1$ and B2 generate a square lattice while A2 and G2 generate a hexagonal lattice, only two of the five possible types of lattices in two dimensions. Whenever Φ is a root system in V, and W is a subspace of V spanned by Ψ = Φ ∩ W, then Ψ is a root system in W. Thus, the exhaustive list of four root systems of rank 2 shows the geometric possibilities for any two roots chosen from a root system of arbitrary rank. In particular, two such roots must meet at an angle of 0, 30, 45, 60, 90, 120, 135, 150, or 180 degrees. Positive roots and simple roots Given a root system Φ we can always choose (in many ways) a set of positive roots. This is a subset Φ + of Φ such that For each root $\alpha\in\Phi$ exactly one of the roots α, –α is contained in Φ + . For any two distinct $\alpha, \beta\in \Phi^+$ such that α + β is a root, $\alpha+\beta\in\Phi^+$. If a set of positive roots Φ + is chosen, elements of –Φ + are called negative roots. An element of Φ + is called a simple root if it cannot be written as the sum of two elements of Φ + . The set Δ of simple roots is a basis of V with the property that every vector in Φ is a linear combination of elements of Δ with all coefficients non-negative, or all coefficients non-positive. For each choice of positive roots, the corresponding set of simple roots is the unique set of roots such that the positive roots are exactly those that can be expressed as a combination of them with non-negative coefficients, and such that these combinations are unique. Dual root system and coroots See also: Langlands dual group If Φ is a root system in V, the coroot αV of a root α is defined by $\alpha^\vee= {2\over (\alpha,\alpha)}\, \alpha.$ The set of coroots also forms a root system ΦV in V, called the dual root system (or sometimes inverse root system). By definition, αV V = α, so that Φ is the dual root system of ΦV. The lattice in V spanned by ΦV is called the coroot lattice. Both Φ and ΦV have the same Weyl group W and, for s in W, $(s\alpha)^\vee= s(\alpha^\vee).$ If Δ is a set of simple roots for Φ, then ΔV is a set of simple roots for ΦV. Classification of root systems by Dynkin diagrams Pictures of all the irreducible Dynkin diagrams Irreducible root systems correspond to certain graphs, the Dynkin diagrams named after Eugene Dynkin. The classification of these graphs is a simple matter of combinatorics, and induces a classification of irreducible root systems. Given a root system, select a set Δ of simple roots as in the preceding section. The vertices of the associated Dynkin diagram correspond to vectors in Δ. An edge is drawn between each non-orthogonal pair of vectors; it is an undirected single edge if they make an angle of 2π / 3 radians, a directed double edge if they make an angle of 3π / 4 radians, and a directed triple edge if they make an angle of 5π / 6 radians. The term "directed edge" means that double and triple edges are marked with an angle sign pointing toward the shorter vector. Although a given root system has more than one possible set of simple roots, the Weyl group acts transitively on such choices. Consequently, the Dynkin diagram is independent of the choice of simple roots; it is determined by the root system itself. Conversely, given two root systems with the same Dynkin diagram, one can match up roots, starting with the roots in the base, and show that the systems are in fact the same. Thus the problem of classifying root systems reduces to the problem of classifying possible Dynkin diagrams. Root systems are irreducible if and only if their Dynkin diagrams are connected. Dynkin diagrams encode the inner product on E in terms of the basis Δ, and the condition that this inner product must be positive definite turns out to be all that is needed to get the desired classification. The actual connected diagrams are as follows. The subscripts indicate the number of vertices in the diagram (and hence the rank of the corresponding irreducible root system). Properties of the irreducible root systems Φ | Φ | | Φ < | I D | W | An (n ≥ 1) n(n + 1)     n + 1 (n + 1)! Bn (n ≥ 2) 2n2 2n 2 2 2n n! Cn (n ≥ 3) 2n2 2n(n − 1) 2 2 2n n! Dn (n ≥ 4) 2n(n − 1)     4 2n − 1 n! E6 72     3 51840 E7 126     2 2903040 E8 240     1 696729600 F4 48 24 4 1 1152 G2 12 6 3 1 12 Irreducible root systems are named according to their corresponding connected Dynkin diagrams. There are four infinite families (An, Bn, Cn, and Dn, called the classical root systems) and five exceptional cases (the exceptional root systems).[1] The subscript indicates the rank of the root system. In an irreducible root system there can be at most two values for the length (α, α)1/2, corresponding to short and long roots. If all roots have the same length they are taken to be long by definition and the root system is said to be simply laced; this occurs in the cases A, D and E. Any two roots of the same length lie in the same orbit of the Weyl group. In the non-simply laced cases B, C, G and F, the root lattice is spanned by the short roots and the long roots span a sublattice, invariant under the Weyl group, equal to r2/2 times the coroot lattice, where r is the length of a long root. In the table to the right, |Φ < | denotes the number of short roots, I denotes the index in the root lattice of the sublattice generated by long roots, D denotes the determinant of the Cartan matrix, and |W| denotes the order of the Weyl group. Explicit construction of the irreducible root systems An A3  1 −1   0   0  0   1 −1   0  0   0   1 −1 Let V be the subspace of Rn+1 for which the coordinates sum to 0, and let Φ be the set of vectors in V of length √2 and which are integer vectors, i.e. have integer coordinates in Rn+1. Such a vector must have all but two coordinates equal to 0, one coordinate equal to 1, and one equal to –1, so there are n2 + n roots in all. One choice of simple roots expressed in the standard basis is: αi = ei – ei+1, for 1 ≤ i ≤ n. The reflection σi through the hyperplane perpendicular to αi is the same as permutation of the adjacent i-th and (i + 1)-th coordinates. Such transpositions generate the full permutation group. For adjacent simple roots, σi(αi+1) = αi+1 + αi = σi+1(αi) = αi + αi+1, that is, reflection is equivalent to adding a multiple of 1; but reflection of a simple root perpendicular to a nonadjacent simple root leaves it unchanged, differing by a multiple of 0. Bn B4  1 -1 0 0 0   1 -1 0 0 0   1 -1 0 0 0   1 Let V = Rn, and let Φ consist of all integer vectors in V of length 1 or √2. The total number of roots is 2n2. One choice of simple roots is: αi = ei – ei+1, for 1 ≤ i ≤ n – 1 (the above choice of simple roots for An-1), and the shorter root αn = en. The reflection σn through the hyperplane perpendicular to the short root αn is of course simply negation of the nth coordinate. For the long simple root αn-1, σn-1(αn) = αn + αn-1, but for reflection perpendicular to the short root, σn(αn-1) = αn-1 + 2αn, a difference by a multiple of 2 instead of 1. B1 is isomorphic to A1 via scaling by √2, and is therefore not a distinct root system. Cn C4  1 -1 0 0 0   1 -1 0 0 0   1 -1 0 0 0   2 Let V = Rn, and let Φ consist of all integer vectors in V of length √2 together with all vectors of the form 2λ, where λ is an integer vector of length 1. The total number of roots is 2n2. One choice of simple roots is: αi = ei – ei+1, for 1 ≤ i ≤ n – 1 (the above choice of simple roots for An-1), and the longer root αn = 2en. The reflection σn(αn-1) = αn-1 + αn, but σn-1(αn) = αn + 2αn-1. C2 is isomorphic to B2 via scaling by √2 and a 45 degree rotation, and is therefore not a distinct root system. 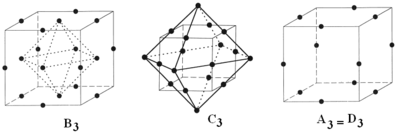Root system B3, C3, and A3=D3 as points within a cube and octahedron Dn D4  1 -1 0 0 0  1 -1 0 0 0  1 -1 0 0  1   1 Let V = Rn, and let Φ consist of all integer vectors in V of length √2. The total number of roots is 2n(n – 1). One choice of simple roots is: αi = ei – ei+1, for 1 ≤ i < n (the above choice of simple roots for An-1) plus αn = en + en-1. Reflection through the hyperplane perpendicular to αn is the same as transposing and negating the adjacent n-th and (n – 1)-th coordinates. Any simple root and its reflection perpendicular to another simple root differ by a multiple of 0 or 1 of the second root, not by any greater multiple. D3 reduces to A3, and is therefore not a distinct root system. D4 has additional symmetry called triality. 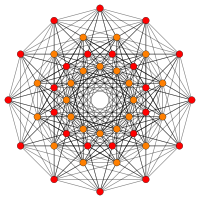E8, E7, E6 72 vertices of 122 represent the root vectors of E6 (Orange nodes are doubled in this E6 Coxeter plane projection) 126 vertices of 231 represent the root vectors of E7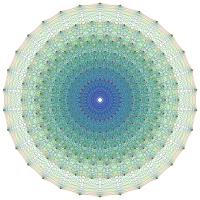 240 vertices of 421 represent the root vectors of E8 The E8 root system is any set of vectors in R8 that is congruent to the following set: D8 ∪ { ½( ∑i=18 εiei) : εi = ±1, ε1•••ε8 = +1}. The root system has 240 roots. The set just listed is the set of vectors of length √2 in the E8 lattice Γ8, which is the set of points in R8 such that: all the coordinates are integers or all the coordinates are half-integers (a mixture of integers and half-integers is not allowed), and the sum of the eight coordinates is an even integer. Thus, E8 = {α ∈ Z8 ∪ (Z+½)8 : |α|2 = ∑αi2 = 2, ∑αi ∈ 2Z}. The root system E7 is the set of vectors in E8 that are perpendicular to a fixed root in E8. The root system E7 has 126 roots. The root system E6 is not the set of vectors in E7 that are perpendicular to a fixed root in E7, indeed, one obtains D6 that way. However, E6 is the subsystem of E8 perpendicular to two suitably chosen roots of E8. The root system E6 has 72 roots. Simple roots in E8: even coordinates 1 -1 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 1 1 0 -½ -½ -½ -½ -½ -½ -½ -½ An alternative description of the E8 lattice which is sometimes convenient is as the set Γ'8 of all points in R8 such that all the coordinates are integers and the sum of the coordinates is even, or all the coordinates are half-integers and the sum of the coordinates is odd. The lattices Γ8 and Γ'8 are isomorphic; one may pass from one to the other by changing the signs of any odd number of coordinates. The lattice Γ8 is sometimes called the even coordinate system for E8 while the lattice Γ'8 is called the odd coordinate system. One choice of simple roots for E8 in the even coordinate system is αi = ei – ei+1, for 1 ≤ i ≤ 6, and α7 = e7 + e6 (the above choice of simple roots for D7) along with α8 = β0 = $-\textstyle\frac{1}{2}(\textstyle \sum_{i=1}^8e_i)$ = (-½,-½,-½,-½,-½,-½,-½,-½). Simple roots in E8: odd coordinates 1 -1 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 1 -1 0 0 0 0 0 0 0 1 -1 -½ -½ -½ -½ -½  ½  ½  ½ One choice of simple roots for E8 in the odd coordinate system is αi = ei – ei+1, for 1 ≤ i ≤ 7 (the above choice of simple roots for A7) along with α8 = β5, where βj = $\textstyle\frac{1}{2}(-\textstyle \sum_{i=1}^je_i+\textstyle \sum_{i=j+1}^8e_i)$. (Using β3 would give an isomorphic result. Using β1,7 or β2,6 would simply give A8 or D8. As for β4, its coordinates sum to 0, and the same is true for α1...7, so they span only the 7-dimensional subspace for which the coordinates sum to 0; in fact –2β4 has coordinates (1,2,3,4,3,2,1) in the basis (αi).) Deleting α1 and then α2 gives sets of simple roots for E7 and E6. Since perpendicularity to α1 means that the first two coordinates are equal, E7 is then the subset of E8 where the first two coordinates are equal, and similarly E6 is the subset of E8 where the first three coordinates are equal. This facilitates explicit definitions of E7 and E6 as: E7 = {α ∈ Z7 ∪ (Z+½)7 : ∑αi2 + α12 = 2, ∑αi + α1 ∈ 2Z}, E6 = {α ∈ Z6 ∪ (Z+½)6 : ∑αi2 + 2α12 = 2, ∑αi + 2α1 ∈ 2Z} F4 Simple roots in F4 1 -1 0 0 0 1 -1 0 0 0 1 0 -½ -½ -½ -½ 48-root vectors of F4, defined by vertices of the 24-cell and its dual, viewed in the Coxeter plane For F4, let V = R4, and let Φ denote the set of vectors α of length 1 or √2 such that the coordinates of 2α are all integers and are either all even or all odd. There are 48 roots in this system. One choice of simple roots is: the choice of simple roots given above for B4, plus α4 = – $\textstyle\frac{1}{2} \sum_{i=1}^4 e_i$. 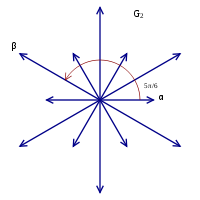G2 Simple roots in G2 1  -1   0 -1 2 -1 The root system G2 has 12 roots, which form the vertices of a hexagram. See the picture above. One choice of simple roots is: (α1, β = α2 – α1) where αi = ei – ei+1 for i = 1, 2 is the above choice of simple roots for A2. Root systems and Lie theory Irreducible root systems classify a number of related objects in Lie theory, notably the simple Lie groups (see the list of simple Lie groups), including the simple complex Lie groups; their associated simple complex Lie algebras; and simply connected complex Lie groups which are simple modulo centers. In each case, the roots are non-zero weights of the adjoint representation. In the case of a simply connected simple compact Lie group G with maximal torus T, the root lattice can naturally be identified with Hom(T, T) and the coroot lattice with Hom(T, T); see Adams (1983). For connections between the exceptional root systems and their Lie groups and Lie algebras see E8, E7, E6, F4, and G2. See also ADE classification Affine root system Coxeter–Dynkin diagram Coxeter group Coxeter matrix Dynkin diagram root datum Weyl group Notes ^ Hall, Brian C. (2003), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Springer, ISBN 0-387-40122-9 . References Adams, J.F. (1983), Lectures on Lie groups, University of Chicago Press, ISBN 0226005305  Bourbaki, Nicolas (2002), Lie groups and Lie algebras, Chapters 4–6 (translated from the 1968 French original by Andrew Pressley), Elements of Mathematics, Springer-Verlag, ISBN 3-540-42650-7 . The classic reference for root systems. Kac, Victor G. (1994), Infinite dimensional Lie algebras . Further reading Dynkin, E. B. The structure of semi-simple algebras. (Russian) Uspehi Matem. Nauk (N.S.) 2, (1947). no. 4(20), 59–127. External links Wikimedia Foundation. 2010. Игры ⚽ Нужно сделать НИР? Chidambaram Subramaniam Pheochromocytoma Look at other dictionaries: Root'System — Pays d’origine  France Genre musical Reggae roots Site officiel http://www.rootsystem.org …   Wikipédia en Français root system — noun a developed system of roots • Syn: ↑rootage • Hypernyms: ↑system, ↑scheme • Part Meronyms: ↑root * * * root system noun • • • …   Useful english dictionary root system — šaknų sistema statusas T sritis ekologija ir aplinkotyra apibrėžtis Augalo šaknų visuma, kurią sudaro pagrindinės (liemeninės arba kuokštinės), šalutinės ir pridėtinės šaknys ir šakniaplaukiai. atitikmenys: angl. root system vok. Wurzelsystem, n; …   Ekologijos terminų aiškinamasis žodynas root system — šaknų sistema statusas T sritis augalininkystė apibrėžtis Augalo šaknų visuma. atitikmenys: angl. root system rus. корневая система …   Žemės ūkio augalų selekcijos ir sėklininkystės terminų žodynas Fibrous root system — A fibrous root system (sometimes also called adventitious root system) is the opposite of a taproot system. It is usually formed by thin, moderately branching roots growing from the stem. A fibrous root system is universal in monocotyledonous… …   Wikipedia Dimorphic root system — A dimorphic root system is a plant root system with two distinct root forms, which are adapted to perform different functions. One of the most common manifestations is in plants with both a taproot, which grows straight down to the water table,… …   Wikipedia Root pressure — Root pressure: osmotic pressure within the cells of a root system that causes sap to rise through a plant stem to the leaves.Root pressure occurs in the xylem of some vascular plants when the soil moisture level is high either at night or when… …   Wikipedia Root hairs — Root hair cells, the rhizoids of many vascular plants, are tubular outgrowths of trichoblasts, the hair forming cells on the epidermis of a plant root. That is, root hair cells are lateral extensions of a single cell and only rarely branched.… …   Wikipedia root pressure — root′ pres sure n. pln the osmotic pressure within the cells of a root system that causes water to rise to stems and leaves • Etymology: 1870–75 …   From formal English to slang root mass — root mass, the lump of earth dug up when transplanting a plant, containing and protecting enough of the root system so that the plant can survive the shock of transplantation …   Useful english dictionary 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”