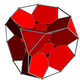
Truncated 24-cell

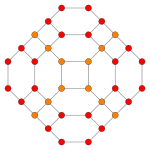
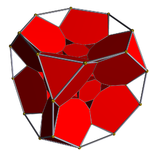
24-cell	Truncated 24-cell	Bitruncated 24-cell
Schlegel diagrams centered on one [3,4] (cells at opposite at [4,3])

In geometry, a truncated 5-cell is a uniform polychoron (4-dimensional uniform polytope) formed as the truncation of the regular 5-cell.

There are two degrees of trunctions, including a bitruncation.

Truncated 5-cell

Truncated 24-cell
Type	Uniform polychoron
Schläfli symbol	t0,1{3,4,3} t0,1,2{3,3,4} t0,1,2,3{31,1,1}
Coxeter-Dynkin diagrams
Cells	48	24 4.6.6 24 4.4.4
Faces	240	144 {4} 96 {6}
Edges	384
Vertices	192
Vertex figure	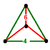equilateral triangular pyramid
Symmetry groups	F4 [3,4,3] B4 [3,3,4] D4 [31,1,1]
Properties	convex zonohedron
Uniform index	23 24 25

The truncated 24-cell is a uniform 4-dimensional polytope (or uniform polychoron), which is bounded by 48 cells: 24 cubes, and 24 truncated octahedra. Each vertex contains three truncated octahedra and one cube, in an equilateral triangular pyramid vertex figure.

Construction

The truncated 24-cell can be constructed from with three symmetry groups:

1. F₄ [3,4,3]: A truncation of the 24-cell.
2. B₄ [3,3,4]: A cantitruncation of the 16-cell, with two families of truncated octahedral cells.
3. D₄ [3^1,1,1]: An omnitruncation of the demitesseract, with three families of truncated octahedral cells.

It is also a zonotope: it can be formed as the Minkowski sum of the six line segments connecting opposite pairs among the twelve permutations of the vector (+1,−1,0,0).

Cartesian coordinates

The Cartesian coordinates of the vertices of a truncated 24-cell having edge length sqrt(2) are all coordinate permutations and sign combinations of:

(0,1,2,3)

The dual configuation has coordinates at all coordinate permutation and signs of

(1,1,1,5)

(1,3,3,3)

(2,2,2,4)

Structure

The 24 cubical cells are joined via their square faces to the truncated octahedra; and the 24 truncated octahedra are joined to each other via their hexagonal faces.

Projections

The parallel projection of the truncated 24-cell into 3-dimensional space, truncated octahedron first, has the following layout:

• The projection envelope is a great rhombicuboctahedron.
• Two of the truncated octahedra project onto a truncated octahedron lying in the center of the envelope.
• Six cuboidal volumes join the square faces of this central truncated octahedron to the center of the octagonal faces of the great rhombicuboctahedron. These are the images of 12 of the cubical cells, a pair of cells to each image.
• The 12 square faces of the great rhombicuboctahedron are the images of the remaining 12 cubes.
• The 6 octagonal faces of the great rhombicuboctahedron are the images of 6 of the truncated octahedra.
• The 8 (non-uniform) truncated octahedral volumes lying between the hexagonal faces of the projection envelope and the central truncated octahedron are the images of the remaining 16 truncated octahedra, a pair of cells to each image.

Images

orthographic projections

Coxeter plane	F4
Graph
Dihedral symmetry	[12]
Coxeter plane	B3 / A2 (a)	B3 / A2 (b)
Graph
Dihedral symmetry	[6]	[6]
Coxeter plane	B4	B2 / A2
Graph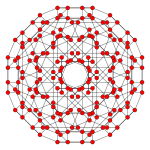
Dihedral symmetry	[8]	[4]

Schlegel diagram (cubic cells visible)	Schlegel diagram 8 of 24 truncated octahedral cells visible	net
Stereographic projection Centered on truncated tetrahedron

Bitruncated 24-cell

Bitruncated 24-cell
Schlegel diagram, centered on truncated cube, with alternate cells hidden
Type	Uniform polychoron
Schläfli symbol	t1,2{3,4,3}
Coxeter-Dynkin diagram
Cells	48 (3.8.8)
Faces	336	192 {3} 144 {8}
Edges	576
Vertices	288
Edge figure	3.8.8
Vertex figure	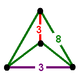tetragonal disphenoid
Symmetry group	F4, [[3,4,3]], order 2304
Properties	convex, isogonal, isotoxal, isochoric
Uniform index	26 27 28

The bitruncated 24-cell is a 4-dimensional uniform polytope (or uniform polychoron) derived from the 24-cell. It is constructed by bitruncating the 24-cell (truncating at halfway to the depth which would yield the dual 24-cell).

Being a uniform polychoron, it is vertex-transitive. In addition, it is cell-transitive, consisting of 48 truncated cubes, and also edge-transitive, with 3 truncated cubes cells per edge and with one triangle and two octagons around each edge.

The 48 cells of the bitruncated 24-cell correspond with the 24 cells and 24 vertices of the 24-cell. As such, the centers of the 48 cells form the root system of type F₄.

Its vertex figure is a tetragonal disphenoid, a tetrahedron with 2 opposite edges length 1 and all 4 lateral edges length sqrt(2+sqrt(2)).

Alternative names

• Bitruncated 24-cell (Norman W. Johnson)
• 48-cell as a cell-transitive 4-polytope
• Bitruncated icositetrachoron
• Bitruncated polyoctahedron
• Tetracontaoctachoron (Cont) (Jonathan Bowers)

Structure

The truncated cubes are joined to each other via their octagonal faces in anti orientation; i. e., two adjoining truncated cubes are rotated 45 degrees relative to each other so that no two triangular faces share an edge.

The sequence of truncated cubes joined to each other via opposite octagonal faces form a cycle of 8. Each truncated cube belongs to 3 such cycles. On the other hand, the sequence of truncated cubes joined to each other via opposite triangular faces form a cycle of 6. Each truncated cube belongs to 4 such cycles.

Coordinates

The Cartesian coordinates of a bitruncated 24-cell having edge length 2 are all permutations of coordinates and sign of:

(0, 2+√2, 2+√2, 2+2√2)

(1, 1+√2, 1+√2, 3+2√2)

Projections

Projection to 2 dimensions

orthographic projections

Coxeter plane	F4	B4
Graph
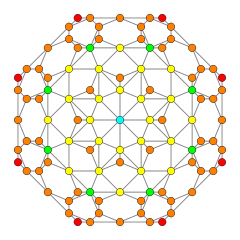
Dihedral symmetry	[[12]]	[8]
Coxeter plane	B3 / A2	B2 / A3
Graph
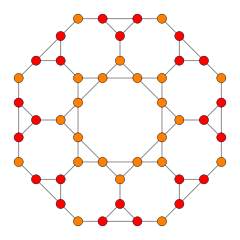
Dihedral symmetry	[6]	[[4]]

Projection to 3 dimensions

Orthographic

Perspective

The following animation shows the orthographic projection of the bitruncated 24-cell into 3 dimensions. The animation itself is a perspective projection from the static 3D image into 2D, with rotation added to make its structure more apparent. The images of the 48 truncated cubes are laid out as follows: The central truncated cube is the cell closest to the 4D viewpoint, highlighted to make it easier to see. To reduce visual clutter, the vertices and edges that lie on this central truncated cube have been omitted. Surrounding this central truncated cube are 6 truncated cubes attached via the octagonal faces, and 8 truncated cubes attached via the triangular faces. These cells have been made transparent so that the central cell is visible. The 6 outer square faces of the projection envelope are the images of another 6 truncated cubes, and the 12 oblong octagonal faces of the projection envelope are the images of yet another 12 truncated cubes. The remaining cells have been culled because they lie on the far side the bitruncated 24-cell, and are obscured from the 4D viewpoint. These include the antipodal truncated cube, which would have projected to the same volume as the highlighted truncated cube, with 6 other truncated cubes surrounding it attached via octagonal faces, and 8 other truncated cubes surrounding it attached via triangular faces.

The following animation shows the cell-first perspective projection of the bitruncated 24-cell into 3 dimensions. Its structure is the same as the previous animation, except that there is some foreshortening due to the perspective projection.

Stereographic projection

Related regular skew polyhedron

The regular skew polyhedron, {8,4|3}, exists in 4-space with 4 octagonal around each vertex, in a zig-zagging nonplanar vertex figure. These octagonal faces can be seen on the bitruncated 24-cell, using all 576 edges and 288 vertices. The 192 triangular faces of the bitruncated 24-cell can be seen as removed. The dual regular skew polyhedron, {4,8|3}, is similarly related to the square faces of the runcinated 24-cell.

Related polytopes

BC₄:

Name	tesseract	rectified tesseract	truncated tesseract	cantellated tesseract	runcinated tesseract	bitruncated tesseract	cantitruncated tesseract	runcitruncated tesseract	omnitruncated tesseract
Coxeter-Dynkin diagram
Schläfli symbol	{4,3,3}	t1{4,3,3}	t0,1{4,3,3}	t0,2{4,3,3}	t0,3{4,3,3}	t1,2{4,3,3}	t0,1,2{4,3,3}	t0,1,3{4,3,3}	t0,1,2,3{4,3,3}
Schlegel diagram
B4 Coxeter plane graph
Name	16-cell	rectified 16-cell	truncated 16-cell	cantellated 16-cell	runcinated 16-cell	bitruncated 16-cell	cantitruncated 16-cell	runcitruncated 16-cell	omnitruncated 16-cell
Coxeter-Dynkin diagram
Schläfli symbol	{3,3,4}	t1{3,3,4}	t0,1{3,3,4}	t0,2{3,3,4}	t0,3{3,3,4}	t1,2{3,3,4}	t0,1,2{3,3,4}	t0,1,3{3,3,4}	t0,1,2,3{3,3,4}
Schlegel diagram
B4 Coxeter plane graph

F₄:

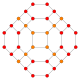
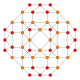
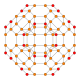
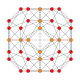
Name	24-cell	truncated 24-cell	rectified 24-cell	cantellated 24-cell	bitruncated 24-cell	cantitruncated 24-cell	runcinated 24-cell	runcitruncated 24-cell	omnitruncated 24-cell	snub 24-cell
Schläfli symbol	{3,4,3}	t0,1{3,4,3}	t1{3,4,3}	t0,2{3,4,3}	t1,2{3,4,3}	t0,1,2{3,4,3}	t0,3{3,4,3}	t0,1,3{3,4,3}	t0,1,2,3{3,4,3}	h0,1{3,4,3}
Coxeter-Dynkin diagram
Schlegel diagram
F4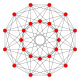
B4
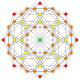
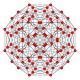
B3(a)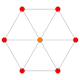
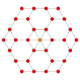
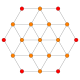
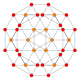
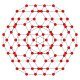
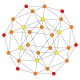
B3(b)
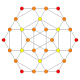
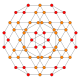
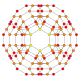
B2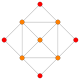

External links

• 3. Convex uniform polychora based on the icositetrachoron (24-cell) - Model 24, 27, George Olshevsky.
• Richard Klitzing, 4D, uniform polytopes (polychora) x3x4o3o - tico, o3x4x3o - cont