- Compound of ten tetrahedra
-
Compound of ten tetrahedra 
Type regular compound Index UC6, W25 Elements
(As a compound)10 tetrahedra:
F = 40, E = 60, V = 20Dual compound Self-dual Symmetry group icosahedral (Ih) Subgroup restricting to one constituent chiral tetrahedral (T) Stellation diagram Stellation core Convex hull 

Icosahedron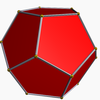
DodecahedronThis polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876.
Contents
As a compound
It can also be seen as the compound of ten tetrahedra with full icosahedral symmetry (Ih). It is one of five regular compounds constructed from identical Platonic solids.
It shares the same vertex arrangement as a dodecahedron.
The compound of five tetrahedra represents two chiral halves of this compound.
As a stellation
This polyhedron is a stellation of the icosahedron, and given as Wenninger model index 25.
As a facetting
It is also a facetting of the dodecahedron, as shown at left.
See also
References
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-52-109859-9.
- Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. (1999). The fifty-nine icosahedra (3rd ed.). Tarquin. ISBN 978-1-899618-32-3. MR676126 (1st Edn University of Toronto (1938))
External links
- Weisstein, Eric W., "Tetrahedron 10-Compound" from MathWorld.
- VRML model: [1]
- Compounds of 5 and 10 Tetrahedra by Sándor Kabai, The Wolfram Demonstrations Project.
Notable stellations of the icosahedron Regular Uniform duals Regular compounds Regular star Others Icosahedron Small triambic icosahedron Great triambic icosahedron Compound of five octahedra Compound of five tetrahedra Compound of ten tetrahedra Great icosahedron Excavated dodecahedron Final stellation 








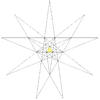
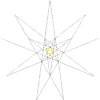

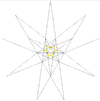
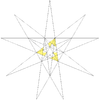

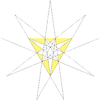


The stellation process on the icosahedron creates a number of related polyhedra and compounds with icosahedral symmetry. 
This polyhedron-related article is a stub. You can help Wikipedia by expanding it.

