- Polyhedral compound
-
A polyhedral compound is a polyhedron that is itself composed of several other polyhedra sharing a common centre. They are the three-dimensional analogs of polygonal compounds such as the hexagram.
Neighbouring vertices of a compound can be connected to form a convex polyhedron called the convex hull. The compound is a facetting of the convex hull.
Another convex polyhedron is formed by the small central space common to all members of the compound. This polyhedron can be considered the core for a set of stellations including this compound. (See List of Wenninger polyhedron models for these compounds and more stellations.)
Contents
Regular compounds
A regular polyhedron compound can be defined as a compound which, like a regular polyhedron, is vertex-transitive, edge-transitive, and face-transitive. With this definition there are 5 regular compounds.
Components Picture Convex hull Core Symmetry Dual Compound of two tetrahedra, or stella octangula 
Cube Octahedron Oh Self-dual Compound of five tetrahedra, or chiro-icosahedron 
Dodecahedron Icosahedron I enantiomorph, or chiral twin Compound of ten tetrahedra, compound of two chiro-icoshedra, or icosiicosahedron 
Dodecahedron Icosahedron Ih Self-dual Compound of five cubes, or rhombihedron 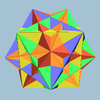
Dodecahedron Rhombic triacontahedron Ih Compound of five octahedra Compound of five octahedra, or small icosiicosahedron 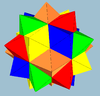
Icosidodecahedron Icosahedron Ih Compound of five cubes Best known is the compound of two tetrahedra, often called the stella octangula, a name given to it by Kepler. The vertices of the two tetrahedra define a cube and the intersection of the two an octahedron, which shares the same face-planes as the compound. Thus it is a stellation of the octahedron, and in fact, the only finite stellation thereof.
The stella octangula can also be regarded as a dual-regular compound.
The compound of five tetrahedra comes in two enantiomorphic versions, which together make up the compound of 10 tetrahedra. Each of the tetrahedral compounds is self-dual, and the compound of 5 cubes is dual to the compound of 5 octahedra.
Dual-regular compounds
A dual-regular compound is composed of a regular polyhedron (one of the Platonic solids or Kepler-Poinsot polyhedra) and its regular dual, arranged reciprocally about a common intersphere or midsphere, such that the edge of one polyhedron intersects the dual edge of the dual polyhedron. There are five such compounds.
Components Picture Convex hull Core Symmetry Compound of two tetrahedra, or Stella octangula 
Cube Octahedron Oh Compound of cube and octahedron 
Rhombic dodecahedron Cuboctahedron Oh Compound of dodecahedron and icosahedron 
Rhombic triacontahedron Icosidodecahedron Ih Compound of great icosahedron and great stellated dodecahedron 
Dodecahedron Icosahedron Ih Compound of small stellated dodecahedron and great dodecahedron 
Icosahedron Dodecahedron Ih The dual-regular compound of a tetrahedron with its dual polyhedron is also the regular Stella octangula, since the tetrahedron is self-dual.
The cube-octahedron and dodecahedron-icosahedron dual-regular compounds are the first stellations of the cuboctahedron and icosidodecahedron, respectively.
The compound of the small stellated dodecahedron and great dodecahedron looks outwardly the same as the small stellated dodecahedron, because the great dodecahedron is completely contained inside. For this reason, the image shown above shows the small stellated dodecahedron in wireframe.
Uniform compounds
Main article: Uniform polyhedron compoundIn 1976 John Skilling published Uniform Compounds of Uniform Polyhedra which enumerated 75 compounds (including 6 as infinite prismatic sets of compounds, #20-#25) made from uniform polyhedra with rotational symmetry. (Every vertex is vertex-transitive and every vertex is transitive with every other vertex.) This list includes the five regular compounds above. [1]
Here is a pictorial table of the 75 uniform compounds as listed by Skilling. Most are singularly colored by each polyhedron element. Some as chiral pairs are colored by symmetry of the faces within each polyhedron.
- 1-19: Miscellaneous (4,5,6,9,17 are the 5 regular compounds)
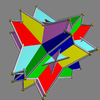

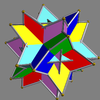



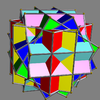
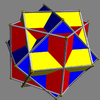
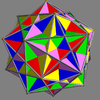
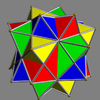
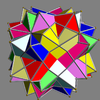
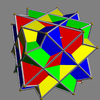


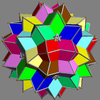
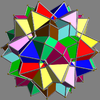

- 20-25: Prism symmetry embedded in prism symmetry,




- 26-45: Prism symmetry embedded in octahedral or icosahedral symmetry,

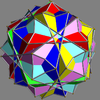

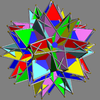






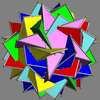





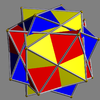
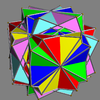


- 46-67: Tetrahedral symmetry embedded in octahedral or icosahedral symmetry,

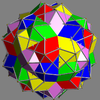

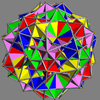

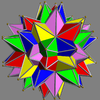







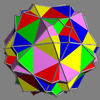
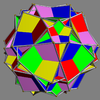
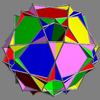



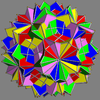
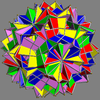

- 68-75: enantiomorph pairs






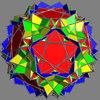
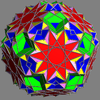
Two polyhedra that are compounds but have their elements rigidly locked into place are the small complex icosidodecahedron (compound of icosahedron and great dodecahedron) and the great complex icosidodecahedron (compound of small stellated dodecahedron and great icosahedron). If the definition of a uniform polyhedron is generalised they are uniform.
Group theory
In terms of group theory, if G is the symmetry group of a polyhedral compound, and the group acts transitively on the polyhedra (so that each polyhedra can be sent to any of the others, as in uniform compounds), then if H is the stabilizer of a single chosen polyhedron, the polyhedra can be identified with the orbit space G/H – the coset gH corresponds to which polyhedron g sends the chosen polyhedron to.
External links
- MathWorld: Polyhedron Compound
- Stella: Polyhedron Navigator - Software used to create the images on this page. Can print nets for many compounds.
- Compound polyhedra – from Virtual Reality Polyhedra
- Skilling's 75 Uniform Compounds of Uniform Polyhedra
- Skilling's Uniform Compounds of Uniform Polyhedra
- Polyhedral Compounds
- http://users.skynet.be/polyhedra.fleurent/Compounds_2/Compounds_2.htm
- Compound of Small Stellated Dodecahedron and Great Dodecahedron {5/2,5}+{5,5/2}
- Compound polyhedra – from Virtual Reality
References
- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society 79: 447–457, doi:10.1017/S0305004100052440, MR0397554.
- Cromwell, Peter R. (1997), Polyhedra, Cambridge.
- Wenninger, Magnus (1983), Dual Models, Cambridge, England: Cambridge University Press, pp. 51–53.
- Harman, Michael G. (circa 1974), Polyhedral Compounds, unpublished manuscript, http://www.georgehart.com/virtual-polyhedra/compounds-harman.html.
- Hess, Edmund (1876), "Zugleich Gleicheckigen und Gleichflächigen Polyeder", Schriften der Gesellschaft zur Berörderung der Gasammten Naturwissenschaften zu Marburg 11: 5–97.
- Pacioli, Luca (1509), De Divina Proportione.
Categories:- Polyhedral compounds
Wikimedia Foundation. 2010.
