- Small complex icosidodecahedron
-
Small complex icosidodecahedron 
Type Uniform star polyhedron Elements F = 32, E = 60 (30x2)
V = 12 (χ = -16)Faces by sides 20{3}+12{5} Wythoff symbol 5 | 3/2 5 Symmetry group Ih, [5,3], *532 Index references U-, C-, W- 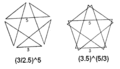
(3/2.5)5
(3.5)5/3
(Vertex figure)
Small complex icosidodecacron
(dual polyhedron)In geometry, the small complex icosidodecahedron is a degenerate uniform star polyhedron. It has 32 faces (20 triangles and 12 pentagons), 60 (doubled) edges and 12 vertices. All edges are doubled (making it degenerate), sharing 4 faces, but are considered as two overlapping edges as topological polyhedron.
It can be constructed from a number of different vertex figures.
As a compound
It can be seen as a compound of the icosahedron {3,5} and the great dodecahedron {5,5/2} where all vertices and edges coincide. The small complex icosidodecahedron appears to be an icosahedron because the great dodecahedron is completely contained inside the icosahedron.
Compound polyhedron 


Icosahedron Great dodecahedron Compound See also
- Great complex icosidodecahedron
- Small complex rhombicosidodecahedron
- Complex rhombidodecadodecahedron
- Great complex rhombicosidodecahedron
References
- Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences 246: 401–450, ISSN 0080-4614, JSTOR 91532, MR0062446 ((Table 6, degenerate cases)
- Weisstein, Eric W., "Small complex icosidodecahedron" from MathWorld.
- Richard Klitzing, 3D uniform polyhedra, x3/2o5o5*a - cid

This geometry-related article is a stub. You can help Wikipedia by expanding it.
