- Great triambic icosahedron
-
Great triambic icosahedron Medial triambic icosahedron 

Types Dual uniform polyhedra Symmetry group Ih Name Great triambic icosahedron Medial triambic icosahedron Index references DU47, W34, 30/59 DU41, W34, 30/59 Elements F = 20, E = 60
V = 32 (χ = -8)F = 20, E = 60
V = 24 (χ = -16)Isohedral faces 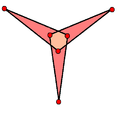
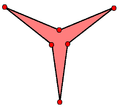
Duals 
Great ditrigonal icosidodecahedron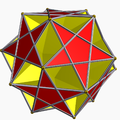
Ditrigonal dodecadodecahedronStellation Icosahedron: W34 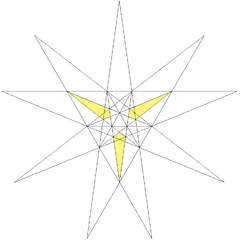
Stellation diagramIn geometry, the great triambic icosahedron and medial triambic icosahedron are visually identical dual uniform polyhedra. The exterior surface also represents the De1f1 stellation of the icosahedron. The only way to differentiate these two polyhedra is to mark which intersections between edges are true vertices and which are not. In the above images, true vertices are marked by gold spheres.
The 12 vertices of the convex hull matches the vertex arrangement of an icosahedron.
Contents
Great triambic icosahedron
The great triambic icosahedron is the dual of the great ditrigonal icosidodecahedron, U47. It has 20 inverted-hexagonal faces, shaped like a three-bladed propeller. It has 32 vertices: 12 exterior points, and 20 hidden inside. It has 60 edges.
Medial triambic icosahedron
The medial triambic icosahedron is the dual of the ditrigonal dodecadodecahedron, U41. It has 20 faces, each being simple concave isogonal hexagons. It has 24 vertices: 12 exterior points, and 12 hidden inside. It has 60 edges.
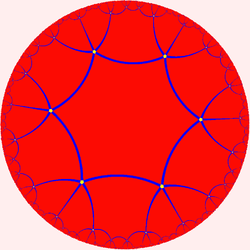
Unlike the great triambic icosahedron, the medial triambic icosahedron is topologically a regular polyhedron of index two.[1] By distorting the triambi into regular hexagons, one obtains the hyperbolic order-5 hexagonal tiling:
As a stellation
It is Wenninger's 34th model in his 9th stellation of the icosahedron
See also
References
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- Wenninger, Magnus (1983). Dual Models. Cambridge University Press. ISBN 978-0-521-54325-5. MR730208.
- ^ The Regular Polyhedra (of index two), David A. Richter
External links
- Weisstein, Eric W., "Great triambic icosahedron" from MathWorld.
- Weisstein, Eric W., "Medial triambic icosahedron" from MathWorld.
- gratrix.net Uniform polyhedra and duals
- bulatov.org Medial triambic icosahedron Great triambic icosahedron
Notable stellations of the icosahedron Regular Uniform duals Regular compounds Regular star Others Icosahedron Small triambic icosahedron Great triambic icosahedron Compound of five octahedra Compound of five tetrahedra Compound of ten tetrahedra Great icosahedron Excavated dodecahedron Final stellation 








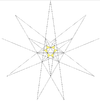
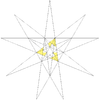

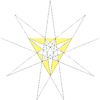
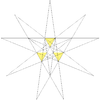

The stellation process on the icosahedron creates a number of related polyhedra and compounds with icosahedral symmetry. 
This geometry-related article is a stub. You can help Wikipedia by expanding it.