Midsphere

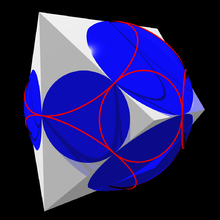A polyhedron and its midsphere. The red circles are the boundaries of spherical caps within which the surface of the sphere can be seen from each vertex.

In geometry, the midsphere or intersphere of a polyhedron is a sphere which is tangent to every edge of the polyhedron. That is to say, it touches any given edge at exactly one point. Not every polyhedron has a midsphere, but for every polyhedron there is a combinatorially equivalent polyhedron, the canonical polyhedron, that does have a midsphere.

The midsphere is so-called because it is between the inscribed sphere (which is tangent to every face of a polyhedron) and the circumscribed sphere (which touches every vertex). The radius of this sphere is called the midradius.

Examples

The uniform polyhedra, including the regular, quasiregular and semiregular polyhedra and their duals all have midspheres. In the regular polyhedra, the inscribed sphere, midsphere, and circumscribed sphere all exist and are concentric.^[1]

Tangent circles

If O is the midsphere of a polyhedron P, then the intersection of O with any face of P is a circle. The circles formed in this way on all of the faces of P form a system of circles on O that are tangent exactly when the faces they lie in share an edge.

Dually, if v is a vertex of P, then there is a cone that has its apex at v and that is tangent to O in a circle; this circle forms the boundary of a spherical cap within which the sphere's surface is visible from the vertex. That is, the circle is the horizon of the midsphere, as viewed from the vertex. The circles formed in this way are tangent to each other exactly when the vertices they correspond to are connected by an edge.

Duality

If a polyhedron P has a midsphere O, then the polar polyhedron with respect to O also has O as its midsphere. The face planes of the polar polyhedron pass through the circles on O that are tangent to cones having the vertices of P as their apexes.^[2]

Canonical polyhedron

One version of the circle packing theorem, on representing planar graphs by systems of tangent circles, states that every polyhedral graph can be represented by a polyhedron with a midsphere. The horizon circles of a canonical polyhedron can be transformed, by stereographic projection, into a collection of circles in the Euclidean plane that do not cross each other and are tangent to each other exactly when the vertices they correspond to are adjacent.^[3] In contrast, there exist polyhedra that do not have an equivalent form with an inscribed sphere or circumscribed sphere.^[4]

Any two polyhedra with the same face lattice and the same midsphere can be transformed into each other by a projective transformation of three-dimensional space that leaves the midsphere in the same position. The restriction of this projective transformation to the midsphere is a Möbius transformation.^[5] There is a unique way of performing this transformation so that the midsphere is the unit sphere and so that the centroid of the points of tangency is at the center of the sphere; this gives a representation of the given polyhedron that is unique up to congruence, the canonical polyhedron.^[6] Alternatively, a transformed polyhedron that maximizes the minimum distance of a vertex from the midsphere can be found in linear time; the canonical polyhedron chosen in this way has maximal symmetry among all choices of the canonical polyhedron.^[7]

Notes

1. ^ Coxeter (1973) states this for regular polyhedra; Cundy & Rollett 1961 for archimedean polyhedra.
2. ^ Coxeter (1973).
3. ^ Schramm (1992); Sachs (1994). Schramm states that the existence of an equivalent polyhedron with a midsphere was claimed by Koebe (1936), but that Koebe only proved this result for polyhedra with triangular faces. Schramm credits the full result to William Thurston, but the relevant portion of Thurston's lecture notes [1] again only states the result explicitly for triangulated polyhedra.
4. ^ Schramm (1992); Steinitz (1928).
5. ^ Sachs (1994).
6. ^ Ziegler (1995).
7. ^ Bern & Eppstein (2001).

References

• Bern, M.; Eppstein, D. (2001), "Optimal Möbius transformations for information visualization and meshing", 7th Worksh. Algorithms and Data Structures, Lecture Notes in Computer Science, 2125, Providence, Rhode Island: Springer-Verlag, pp. 14–25, arXiv:cs.CG/0101006, doi:10.1007/3-540-44634-6_3 .
• Coxeter, H. S. M. (1973), "2.1 Regular polyhedra; 2.2 Reciprocation", Regular Polytopes (3rd ed.), Dover, pp. 16–17, ISBN 0-486-61480-8, http://books.google.com/books?id=iWvXsVInpgMC&lpg=PP1&pg=PA16 .
• Cundy, H. M.; Rollett, A. P. (1961), Mathematical Models (2nd ed.), Oxford University Press, p. 117 .
• Koebe, Paul (1936), "Kontaktprobleme der Konformen Abbildung", Ber. Sächs. Akad. Wiss. Leipzig, Math.-Phys. Kl. 88: 141–164 .
• Sachs, Horst (1994), "Coin graphs, polyhedra, and conformal mapping", Discrete Mathematics 134 (1-3): 133–138, doi:10.1016/0012-365X(93)E0068-F, MR1303402 .
• Schramm, Oded (1992), "How to cage an egg", Inventiones Mathematicae 107 (3): 543–560, doi:10.1007/BF01231901, MR1150601, http://www.kryakin.com/files/Invent_mat_(2_8)/107/107_25.pdf .
• Steinitz, E. (1928), "Über isoperimetrische Probleme bei konvexen Polyedern", Journal für die reine und angewandte Mathematik 159: 133–143 .
• Ziegler, Günter M. (1995), Lectures on Polytopes, Graduate Texts in Mathematics, 152, Springer-Verlag, pp. 117–118, ISBN 038794365X .

External links

• Hart, G. W. (1997), "Calculating canonical polyhedra", Mathematica in Education and Research 6 (3): 5–10, http://library.wolfram.com/infocenter/Articles/2012/ . A Mathematica implementation of an algorithm for constructing canonical polyhedra.
• Weisstein, Eric W., "Midsphere" from MathWorld.