Order-7 triangular tiling

Order-7 triangular tiling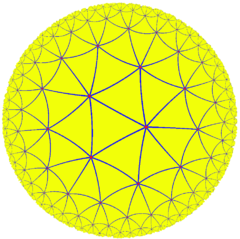
Order-7 triangular tiling
Order-7 triangular tiling
Poincaré disk model of the hyperbolic plane
Type Regular hyperbolic tiling
Vertex figure 37
Schläfli symbol(s) {3,7}
Wythoff symbol(s) 7 | 3 2
Coxeter-Dynkin(s) CDel node.pngCDel 7.pngCDel node.pngCDel 3.pngCDel node 1.png
Coxeter group [7,3]
Dual Order-3 heptagonal tiling
Properties Vertex-transitive, edge-transitive, face-transitive

In geometry, the order-7 triangular tiling is a regular tiling of the hyperbolic plane with a Schläfli symbol of {3,7}.

Contents

Related polyhedra and tiling

This tiling is topologically related as a part of sequence of regular polyhedra with Schläfli symbol {3,p}.

Uniform polyhedron-33-t2.png
{3,3}		 Uniform polyhedron-43-t2.png
{3,4}		 Uniform polyhedron-53-t2.png
{3,5}
Uniform polyhedron-63-t2.png
{3,6}		 Uniform tiling 73-t2.png
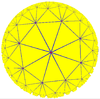
{3,7}		 Uniform tiling 83-t2.png
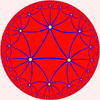
{3,8}		 Uniform tiling 39-t0.png
{3,9}

The dual tiling is the order-3 heptagonal tiling.

Uniform tiling 73-t0.png
order-3 heptagonal tiling		 Uniform tiling 73-t2.png
order-7 triangular tiling

Wythoff constructions yields further uniform tilings, yielding eight uniform tilings, including the two regular ones given here.

Hurwitz surfaces

The symmetry group of the order-7 triangular tiling has fundamental domain the (2,3,7) Schwarz triangle, which yields this tiling.
Further information: Hurwitz surface

The symmetry group of the tiling is the (2,3,7) triangle group, and a fundamental domain for this action is the (2,3,7) Schwarz triangle. This is the smallest hyperbolic Schwarz triangle, and thus, by the proof of Hurwitz's automorphisms theorem, the tiling is the universal tiling that covers all Hurwitz surfaces (the Riemann surfaces with maximal symmetry group), giving them a triangulation whose symmetry group equals their automorphism group as Riemann surfaces.

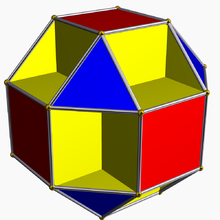The small cubicuboctahedron is a polyhedral immersion of the Klein quartic,[1] which, like all Hurwitz surfaces, is a quotient of this tiling.

The smallest of these is the Klein quartic, the most symmetric genus 3 surface, together with a tiling by 56 triangles, meeting at 24 vertices, with symmetry group the simple group of order 168, known as PSL(2,7). The resulting surface can in turn be polyhedrally immersed into Euclidean 3-space, yielding the small cubicuboctahedron.[1]

The dual order-3 heptagonal tiling has the same symmetry group, and thus yields heptagonal tilings of Hurwitz surfaces.

References

  1. ^ a b (Richter) Note each face in the polyhedron consist of multiple faces in the tiling – two triangular faces constitute a square face and so forth, as per this explanatory image.

See also

External links

Stub icon This geometry-related article is a stub. You can help Wikipedia by expanding it.