Schwarz triangle

In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in (Schwarz 1873).

These can be defined more generally as tessellations of the sphere, the Euclidean plane, or the hyperbolic plane. Each Schwarz triangle on a sphere defines a finite group, while on the Euclidean or hyperbolic plane they define an infinite group.

A Schwarz triangle is represented by three rational numbers (p q r) each representing the angle at a vertex. The value n/d means the vertex angle is d/n of the half-circle. "2" means a right triangle. In case these are whole numbers, the triangle is called a Möbius triangle, and corresponds to a non-overlapping tiling, and the symmetry group is called a triangle group. In the sphere there are 3 Möbius triangles plus 1 1-parameter family; in the plane there are 3 Möbius triangles, while in hyperbolic space there is a 3-parameter family of Möbius triangles, and no exceptional objects.

Solution space

A fundamental domain triangle, (p q r), can exist in different space depending on this constraint:

1 / p + 1 / q + 1 / r > 1 : Spherical

1 / p + 1 / q + 1 / r = 1 : Euclidean plane

1 / p + 1 / q + 1 / r < 1 : Hyperbolic plane

Graphical representation

A Schwarz triangle is represented graphically by a triangular graph. Each node represents an edge (mirror) of the Schwarz triangle. Each edge is labeled by a rational value corresponding to the reflection order, being π/vertex angle.

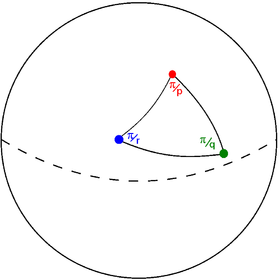
Schwarz triangle (p q r) on sphere

Schwarz triangle graph

Order 2 edges represents perpendicular mirrors which can be ignored in this diagram. The Coxeter-Dynkin diagram represents this triangular graph with order-2 edges hidden.

A Coxeter group can be used for a simpler notation, as (p q r) for cyclic graphs, and (p q 2) = [p,q] for (right triangles), and (p 2 2) = [p]×[].

A list of Schwarz triangles

Möbius triangles for the sphere

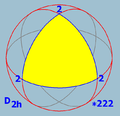
(2 2 2) or [2,2]	(3 2 2) or [3,2]	...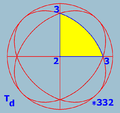
(3 3 2) or [3,3]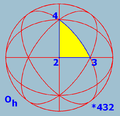	(4 3 2) or [4,3]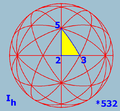	(5 3 2) or [5,3]

Schwarz triangles with whole numbers, also called Möbius triangles, include one 1-parameter family and three exceptional cases:

1. [p,2] or (p 2 2) - Dihedral symmetry,
2. [3,3] or (3 3 2) - Tetrahedral symmetry,
3. [4,3] or (4 3 2) - Octahedral symmetry,
4. [5,3] or (5 3 2) - Icosahedral symmetry,

Schwarz triangles for the sphere by density

The Schwarz triangles (p q r), grouped by density:

Density	Schwarz triangle
1	(2 3 3), (2 3 4), (2 3 5), (2 2 n)
d	(2 2 n/d)
2	(3/2 3 3), (3/2 4 4), (3/2 5 5), (5/2 3 3)
3	(2 3/2 3), (2 5/2 5)
4	(3 4/3 4), (3 5/3 5)
5	(2 3/2 3/2), (2 3/2 4)
6	(3/2 3/2 3/2), (5/2 5/2 5/2), (3/2 3 5), (5/4 5 5)
7	(2 3 4/3), (2 3 5/2)
8	(3/2 5/2 5)
9	(2 5/3 5)
10	(3 5/3 5/2), (3 5/4 5)
11	(2 3/2 4/3), (2 3/2 5)
13	(2 3 5/3)
14	(3/2 4/3 4/3), (3/2 5/2 5/2), (3 3 5/4)
16	(3 5/4 5/2)
17	(2 3/2 5/2)
18	(3/2 3 5/3), (5/3 5/3 5/2)
19	(2 3 5/4)
21	(2 5/4 5/2)
22	(3/2 3/2 5/2)
23	(2 3/2 5/3)
26	(3/2 5/3 5/3)
27	(2 5/4 5/3)
29	(2 3/2 5/4)
32	(3/2 5/45/3)
34	(3/2 3/2 5/4)
38	(3/2 5/4 5/4)
42	(5/4 5/4 5/4)

Triangles for the Euclidean plane

(3 3 3)

(4 4 2)

(6 3 2)

Density 1:

1. (3 3 3) – 60-60-60 (equilateral)
2. (4 4 2) – 45-45-90 (isosceles right)
3. (6 3 2) – 30-60-90

Rational solutions by density:

• Density 0: (4 4/3 ∞), (3 3/2 ∞), (6 6/5 ∞)
• Density 1: (4/3 4/3 2), (4/3 4 2), (6 3/2 2)
• Density 2: (6/5 3 2), (6 6 3/2), (6 6/5 3)

Triangles for the hyperbolic plane

(7 3 2)	(8 3 2)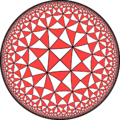	(5 4 2)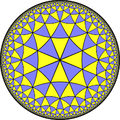
(4 3 3)	(4 4 3)	(∞ ∞ ∞)
Fundamental domains of (p q r) triangles

Density 1:

• (2 3 7), (2 3 8), (2 3 9) ... (2 3 ∞)
• (2 4 5), (2 4 6), (2 4 7) ... (2 4 ∞)
• (2 5 5), (2 5 6), (2 5 7) ... (2 5 ∞)
• (2 6 6), (2 6 7), (2 6 8) ... (2 6 ∞)
• (3 3 4), (3 3 5), (3 3 6) ... (3 3 ∞)
• (3 4 4), (3 4 5), (3 4 6) ... (3 4 ∞)
• (3 5 5), (3 5 6), (3 5 7) ... (3 5 ∞)
• (3 6 6), (3 6 7), (3 6 8) ... (3 6 ∞)
• ...
• (∞ ∞ ∞)

The (2 3 7) Schwarz triangle is the smallest hyperbolic Schwarz triangle, and as such is of particular interest. Its triangle group (or more precisely the index 2 von Dyck group of orientation-preserving isometries) is the (2,3,7) triangle group, which is the universal group for all Hurwitz groups – maximal groups of isometries of Riemann surfaces. All Hurwitz groups are quotients of the (2,3,7) triangle group, and all Hurwitz surfaces are tiled by the (2,3,7) Schwarz triangle. The smallest Hurwitz group is the simple group of order 168, the second smallest non-abelian simple group, which is isomorphic to PSL(2,7), and the associated Hurwitz surface (of genus 3) is the Klein quartic.

The (2 3 8) triangle tiles the Bolza surface, a highly symmetric (but not Hurwitz) surface of genus 2.

See also

• Wythoff symbol
• Wythoff construction
• Uniform polyhedron
• Nonconvex uniform polyhedron
• Polytope density
• Goursat tetrahedron
• Regular hyperbolic tiling
• Uniform tilings in hyperbolic plane

References

• Coxeter, Regular Polytopes, Third edition, (1973), Dover edition, ISBN 0-486-61480-8 (Table 3: Schwarz's Triangles)
• Schwarz, H. A. Zur Theorie der hypergeometrischen Reihe. J. reine angew. Math. 75, 1873. (pages 292-335)
• Wenninger, Magnus J. (1979), "An introduction to the notion of polyhedral density", Spherical models, CUP Archive, pp. 132–134, ISBN 978-0-52122279-2 

External links

• Weisstein, Eric W., "Schwarz triangle" from MathWorld.
• The general Schwarz triangle (p q r) and the generalized incidence matrices of the corresponding polyhedra