Median (geometry)

For another use of the term median in geometry, see Geometric median.

The triangle medians and the centroid.

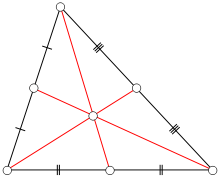
In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposing side. Every triangle has exactly three medians; one running from each vertex to the opposite side. The median bisects the vertex angle from which it is drawn in case of isosceles and equilateral triangles.

Relation to center of mass

Each median of a triangle passes through the triangle's centroid, which is the center of mass of an object of uniform density in the shape of the triangle. Thus the object would balance on any line through the centroid, including any median.

Equal-area division

Each median divides the area of the triangle in half; hence the name. (Any other lines which divide the area of the triangle into two equal parts do not pass through the centroid.)[1] The three medians divide the triangle into six smaller triangles of equal area.

Proof

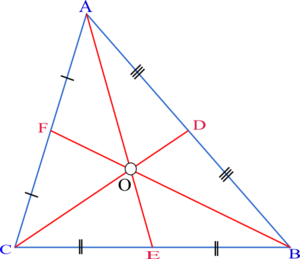
Consider a triangle ABC Let D be the midpoint of $\overline{AB}$, E be the midpoint of $\overline{BC}$, F be the midpoint of $\overline{AC}$, and O be the centroid.

By definition, $AD=DB, AF=FC, BE=EC \,$. Thus [ADO] = [BDO],[AFO] = [CFO],[BEO] = [CEO], and $[ABE]=[ACE] \,$, where [ABC] represents the area of triangle $\triangle ABC$ ; these hold because in each case the two triangles have bases of equal length and share a common altitude from the (extended) base, and a triangle's area equals one-half its base times its height.

We have:

$[ABO]=[ABE]-[BEO] \,$

$[ACO]=[ACE]-[CEO] \,$

Thus, $[ABO]=[ACO] \,$ and $[ADO]=[DBO], [ADO]=\frac{1}{2}[ABO]$

Since $[AFO]=[FCO], [AFO]= \frac{1}{2}ACO=\frac{1}{2}[ABO]=[ADO]$, therefore, $[AFO]=[FCO]=[DBO]=[ADO]\,$. Using the same method, you can show that $[AFO]=[FCO]=[DBO]=[ADO]=[BEO]=[CEO] \,$.

Formulas involving the medians' lengths

The lengths of the medians can be obtained from Apollonius' theorem as:

$m_a = \sqrt {\frac{2 b^2 + 2 c^2 - a^2}{4} },$

$m_b = \sqrt {\frac{2 a^2 + 2 c^2 - b^2}{4} },$

$m_c = \sqrt {\frac{2 a^2 + 2 b^2 - c^2}{4} },$

where a, b and c are the sides of the triangle with respective medians m_a, m_b, and m_c from their midpoints.

Thus we have the relationships:^[1]

$a = \frac{2}{3} \sqrt{-m_a^2 + 2m_b^2 + 2m_c^2} = \sqrt{2(b^2+c^2)-4m_a^2} = \sqrt{\frac{b^2}{2} - c^2 + 2m_b^2} = \sqrt{\frac{c^2}{2} - b^2 + 2m_c^2},$

$b = \frac{2}{3} \sqrt{-m_b^2 + 2m_a^2 + 2m_c^2} = \sqrt{2(a^2+c^2)-4m_b^2} = \sqrt{\frac{a^2}{2} - c^2 + 2m_a^2} = \sqrt{\frac{c^2}{2} - a^2 + 2m_c^2},$

$c = \frac{2}{3} \sqrt{-m_c^2 + 2m_b^2 + 2m_a^2} = \sqrt{2(b^2+a^2)-4m_c^2} = \sqrt{\frac{b^2}{2} - a^2 + 2m_b^2} = \sqrt{\frac{a^2}{2} - b^2 + 2m_a^2}.$

Other properties

For any triangle,^[2]

$\tfrac{3}{4}$(perimeter) < sum of the medians < $\tfrac{3}{2}$(perimeter).

For any triangle with sides a,b,c and medians m_a,m_b,m_c,^[2]

$\tfrac{3}{4}(a^2+b^2+c^2)=m_a^2+m_b^2+m_c^2.$

See also

• Angle bisector
• Altitude (triangle)

References

1. ^ Déplanche, Y. (1996). Diccio fórmulas. Medianas de un triángulo. Edunsa. p. 22. ISBN 9788477471196. http://books.google.com/books?id=1HVHOwAACAAJ. Retrieved 2011-04-24. 
2. ^ ^{a b} Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, Dover, 1996: pp. 86-87.

External links

• Medians and Area Bisectors of a Triangle
• The Medians at cut-the-knot
• Area of Median Triangle at cut-the-knot
• Medians of a triangle With interactive animation
• Constructing a median of a triangle with compass and straightedge animated demonstration
• Weisstein, Eric W., "Triangle Median" from MathWorld.