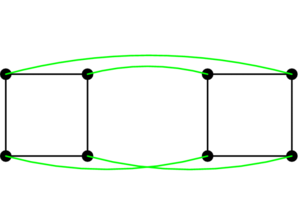
Hypercube graph

Hypercube graph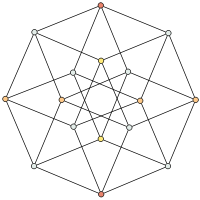
The hypercube graph Q4
Vertices	2n
Edges	2n−1n
Diameter	n
Girth	4 if n≥2
Chromatic number	2
Spectral Gap	$\frac{2}{n}$
Properties	Symmetric Distance regular Unit distance Hamiltonian
Notation	Qn
v · graph theory, the hypercube graph Qn is a regular graph with 2n vertices, which correspond to the subsets of a set with n elements. Two vertices labelled by subsets W and B are joined by an edge if and only if W can be obtained from B by adding or removing a single element. Each vertex of Qn is incident to exactly n edges (that is, Qn is n-regular), so, by the handshaking lemma the total number of edges is 2n−1n. The name comes from the fact that the hypercube graph is the one-dimensional skeleton of the geometric hypercube. Hypercube graphs should not be confused with cubic graphs, which are graphs that are 3-regular. The only hypercube that is a cubic graph is Q3. Construction An animation showing the construction of a hypercube graph of dimension 4 The hypercube graph Qn may be constructed using 2n vertices labeled 0,1,2,...,2n-1 and connecting two vertices whenever their Hamming distance equals 1. Additionally Qn+1 may be constructed using two hypercubes Qn and joining equivalent vertices together as shown in the above picture. The joining edges are called the (n+1)th dimension of Qn. Each dimension of Qn forms a perfect matching. Another definition of Qn is the Cartesian product of n two-vertex complete graphs K2. Inductive construction of Q3 using two Q2 hypercubes. Properties Hamiltonicity It is a well known fact that every hypercube Qn is Hamiltonian for n > 1. Additionally, a Hamiltonian path exists between vertices u,v iff u,v are part of different bipartitions. Both facts are easy to prove using the principle of induction and the inductive construction of hypercube graphs. Hamiltonicity of the hypercube is tightly related to the theory of Gray codes. More precisely there is a bijective correspondence between the set of n-bit cyclic Gray codes and the set of Hamiltonian cycles in the hypercube Qn.[1] An analogous property holds for acyclic n-bit Gray codes and Hamiltonian paths. A lesser known fact is that every perfect matching in the hypercube extends to a Hamiltonian cycle.[2] The question whether every matching extends to a Hamiltonian cycle remains an open problem.[3] Bipartiteness Every hypercube is a bipartite graph. If the function s(x) represents the number of set bits in the binary representation of x, then (assuming the vertices are labeled 0,1,...,2n-1 as in the definition) $c(v) := s(v) \mod 2$ defines a proper two coloring of Qn. Other properties The hypercube graph Qn (n > 1) : is the Hasse diagram of a finite Boolean algebra. is a median graph. Every median graph is an isometric subgraph of a hypercube, and can be formed as a retraction of a hypercube. has more than 22n-2 perfect matchings. (this is another consequence that follows easily from the inductive construction.) is arc transitive and symmetric. The symmetries of hypercube graphs can be represented as signed permutations. contains all the cycles of length 4,6,...,2n-2,2n and is thus a bi-panicyclic graph. can be drawn as a unit distance graph in the Euclidean plane by choosing a unit vector for each set element and placing each vertex corresponding to a set S at the sum of the vectors in S. is a n-vertex-connected graph, by Balinski's theorem is planar (can be drawn with no crossings) if and only if n ≤ 3. The family Qn (n > 1) is a Lévy family of graphs The achromatic number of Qn is known to be proportional to $\sqrt{n2^n}$, but the constant of proportionality is not known precisely.[4] The bandwidth of Qn is exactly $\sum_{i=0}^n \binom{n}{\lfloor n/2\rfloor}$.[5] The eigenvalues of the adjacency matrix are (-n,-n+2,...,-2,0,2,...,n-2,n) and the eigenvalues of its Laplacian are (0,2,...,2n). The k-th eigenvalue has multiplicity $\binom{n}{k}$ in both cases. The isoperimetric number is h(G)=1 Problems The problem of finding the longest path or cycle that is an induced subgraph of a given hypercube graph is known as the snake-in-the-box problem. Szymanski's conjecture concerns the suitability of a hypercube as an network topology for communications. It states that, no matter how one chooses a permutation connecting each hypercube vertex to another vertex with which it should be connected, there is always a way to connect these pairs of vertices by paths that do not share any directed edge.[6] Examples The graph Q0 consists of a single vertex, while Q1 is the complete graph on two vertices and Q2 is a cycle of length 4. The graph Q3 is the 1-skeleton of a cube, a planar graph with eight vertices and twelve edges. The graph Q4 is the Levi graph of the Möbius configuration. See also Cube-connected cycles Fibonacci cube Folded cube graph Notes ^ Mills, W. H. (1963), "Some complete cycles on the n-cube", Proceedings of the American Mathematical Society (American Mathematical Society) 14 (4): 640–643, doi:10.2307/2034292, JSTOR 2034292 . ^ Fink, J. (2007), "Perfect matchings extend to Hamiltonian cycles in hypercubes", Journal of Combinatorial Theory, Series B 97 (6): 1074–1076, doi:10.1016/j.jctb.2007.02.007 . ^ Ruskey, F. and Savage, C. Matchings extend to Hamiltonian cycles in hypercubes on Open Problem Garden. 2007. ^ Roichman, Y. (2000), "On the Achromatic Number of Hypercubes", Journal of Combinatorial Theory, Series B 79 (2): 177–182, doi:10.1006/jctb.2000.1955 . ^ Optimal Numberings and Isoperimetric Problems on Graphs, L.H. Harper, Journal of Combinatorial Theory, 1, 385–393, doi:10.1016/S0021-9800(66)80059-5 ^ Szymanski, Ted H. (1989), "On the Permutation Capability of a Circuit-Switched Hypercube", Proc. Internat. Conf. on Parallel Processing, 1, Silver Spring, MD: IEEE Computer Society Press, pp. 103–110 . References Harary, F.; Hayes, J. P.; Wu, H.-J. (1988), "A survey of the theory of hypercube graphs", Computers & Mathematics with Applications 15 (4): 277–289, doi:10.1016/0898-1221(88)90213-1 . Wikimedia Foundation. 2010. Игры ⚽ Нужна курсовая? Campospinoso Margita Look at other dictionaries: Hypercube (Graphe) — Pour les articles homonymes, voir Hypercube (homonymie).   Cette page se comprend mieux après la lecture de Théorie des graphes. Hypercube …   Wikipédia en Français Hypercube — This article is about the mathematical concept. For the film, see Cube 2: Hypercube. Perspective projections Cube (3 cube) Tesseract (4 cube) In geometry, a hypercube is an n dimensional analogue of a …   Wikipedia Hypercube (graphe) — Pour les articles homonymes, voir Hypercube (homonymie).   Cette page se comprend mieux après la lecture de Théorie des graphes. Hypercube …   Wikipédia en Français Hypercube — Pour les articles homonymes, voir Hypercube (homonymie). Une projection d un hypercube (dans une image bidimensionnelle) Un hypercube est, en géométrie, un analogue …   Wikipédia en Français Median graph — The median of three vertices in a median graph In mathematics, and more specifically graph theory, a median graph is an undirected graph in which any three vertices a, b, and c have a unique median: a vertex m(a,b,c) that belongs to shortest… …   Wikipedia Möbius–Kantor graph — Named after August Ferdinand Möbius and S. Kantor Vertices 16 …   Wikipedia Clebsch graph — Named after Alfred Clebsch Vertices 16 Edges 40 …   Wikipedia Unit distance graph — In mathematics, and particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points by an edge whenever the distance between the two points is exactly one.… …   Wikipedia Universal graph — In mathematics, a universal graph is an infinite graph that contains every finite (or at most countable) graph as an induced subgraph. A universal graph of this type was first constructed by R. Rado [cite journal author = Rado, R. title =… …   Wikipedia Bivariegated graph — In graph theory, a mathematical discipline, a bivariegated graph is a graph whose vertex set can be partitioned into two equal parts such that each vertex is adjacent to exactly one vertex from the other set not containing… …   Wikipedia 18+ © Academic, 2000-2024 Contact us: Technical Support, Advertising Dictionaries export, created on PHP, Joomla, Drupal, WordPress, MODx. Mark and share Search through all dictionaries Translate… Search Internet Share the article and excerpts Direct link … Do a right-click on the link above and select “Copy Link”