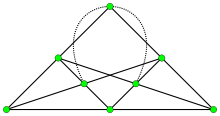
Möbius–Kantor graph

Möbius–Kantor graph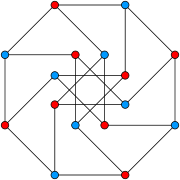
Möbius–Kantor graph
Möbius–Kantor unit distance.svg
Named after August Ferdinand Möbius and S. Kantor
Vertices 16
Edges 24
Radius 4
Diameter 4
Girth 6
Automorphisms 96
Chromatic number 2
Chromatic index 3
Genus 1
Properties Symmetric
Hamiltonian
Bipartite
Cubic
Unit distance
Cayley graph
Perfect
v · mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor. It can be defined as the generalized Petersen graph G(8,3): that is, it is formed by the vertices of an octagon, connected to the vertices of an eight-point star in which each point of the star is connected to the points three steps away from it.

Contents

Möbius–Kantor configuration

The Möbius–Kantor configuration.

Möbius (1828) asked whether there exists a pair of polygons with p sides each, having the property that the vertices of one polygon lie on the lines through the edges of the other polygon, and vice versa. If so, the vertices and edges of these polygons would form a projective configuration. For p = 4 there is no solution in the Euclidean plane, but Kantor (1882) found pairs of polygons of this type, for a generalization of the problem in which the points and edges belong to the complex projective plane. That is, in Kantor's solution, the coordinates of the polygon vertices are complex numbers. Kantor's solution for p = 4, a pair of mutually-inscribed quadrilaterals in the complex projective plane, is called the Möbius–Kantor configuration. Coxeter (1950) supplies the following simple complex projective coordinates for the eight points of the Möbius–Kantor configuration:

(1,0,0), (0,0,1), (ω, −1, 1), (−1, 0, 1),
(−1,ω2,1), (1,ω,0), (0,1,0), (0,−1,1),

where ω denotes the complex cube root of 1.

More abstractly, the Möbius–Kantor configuration can be described as a system of eight points and eight triples of points such that each point belongs to exactly three of the triples. Any two systems of this type are equivalent under some permutation of the points; that is, the Möbius–Kantor configuration is the unique projective configuration of type (8383). The Möbius–Kantor graph derives its name from being the Levi graph of the Möbius–Kantor configuration. It has one vertex per point and one vertex per triple, with an edge connecting two vertices if they correspond to a point and to a triple that contains that point.

The solution to Möbius' problem of mutually inscribed polygons for values of p greater than four is also of interest. In particular, one possible solution for p = 5 is the Desargues configuration, a set of ten points and ten lines, three points per line and three lines per point, that does admit a Euclidean realization. The Möbius configuration is a three-dimensional analogue of the Möbius–Kantor configuration consisting of two mutually inscribed tetrahedra.

Relation to hypercube

The Möbius–Kantor graph is a subgraph of the four-dimensional hypercube graph, formed by removing eight edges from the hypercube (Coxeter 1950). Since the hypercube is a unit distance graph, the Möbius–Kantor graph can also be drawn in the plane with all edges unit length, although such a drawing will necessarily have some pairs of crossing edges.

Topology

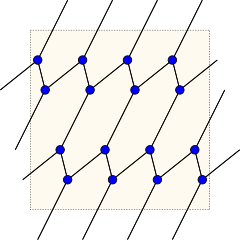The Möbius–Kantor graph, embedded on the torus. Edges extending upwards from the central square should be viewed as connecting with the corresponding edge extending downwards from the square, and edges extending leftwards from the square should be viewed as connecting with the corresponding edge extending rightwards.
"Tucker's Genus Two Group", sculpture by DeWitt Godfrey and Duane Martinez, showing the symmetries of the Möbius–Kantor graph.

The Möbius–Kantor graph cannot be embedded without crossings in the plane; it has crossing number 4, and is the smallest cubic graph with that crossing number (sequence A110507 in OEIS). Additionally, it provides an example of a graph all of whose subgraphs' crossing numbers differ from it by two or more.[1] However, it is a toroidal graph: it has an embedding in the torus in which all faces are hexagons (Marušič & Pisanski 2000).

There is an even more symmetric embedding of Möbius–Kantor graph in the double torus which is a regular map, with six octagonal faces, in which all 96 symmetries of the graph can be realized as symmetries of the embedding; Coxeter (1950) credits this embedding to Threlfall (1932). Its 96-element symmetry group has a Cayley graph that can itself be embedded on the double torus, and was shown by Tucker (1984) to be the unique group with genus two. The Cayley graph on 96 vertices is a flag graph of the genus 2 regular map having Möbius–Kantor graph as a sekeleton. This means it can be obtained from the regular map as a skeleton of the dual of its barycentric subdivision. A sculpture by DeWitt Godfrey and Duane Martinez showing the double torus embedding of the symmetries of the Möbius–Kantor graph was unveiled at the Technical Museum of Slovenia as part of the 6th Slovenian International Conference on Graph Theory in 2007.

The Möbius–Kantor graph admits an embedding into a triple torus (genus 3 torus) that is a regular map having four 12-gonal faces; (Marušič & Pisanski 2000).

Lijnen & Ceulemans (2004), motivated by an investigation of potential chemical structures of carbon compounds, studied the family of all embeddings of the Möbius–Kantor graph onto 2-manifolds; they showed that there are 759 inequivalent embeddings.

Algebraic properties

The automorphism group of the Möbius–Kantor graph is a group of order 96.[2] It acts transitively on the vertices, on the edges and on the arcs of the graph. Therefore the Möbius–Kantor graph is a symmetric graph. It has automorphisms that take any vertex to any other vertex and any edge to any other edge. According to the Foster census, the Möbius–Kantor graph is the unique cubic symmetric graph with 16 vertices, and the smallest cubic symmetric graph which is not also distance-transitive.[3] The Möbius–Kantor graph is also a Cayley graph.

The generalized Petersen graph G(n,k) is vertex-transitive if and only if n = 10 and k =2 or if k2 ≡ ±1 (mod n) and is edge-transitive only in the following seven cases: (n,k) = (4,1), (5,2), (8,3), (10,2), (10,3), (12,5), or (24,5) (Frucht, Graver & Watkins 1971). So the Möbius–Kantor graph is one of only seven symmetric Generalized Petersen graphs. Its symmetric double torus embedding is correspondingly one of only seven regular cubic maps in which the total number of vertices is twice the number of vertices per face (McMullen 1992). Among the seven symmetric generalized Petersen graphs are the cubical graph G(4,1), the Petersen graph G(5,2), the dodecahedral graph G(10,2), the Desargues graph G(10,3) and the Nauru graph G(12,5).

The characteristic polynomial of the Möbius–Kantor graph is equal to

(x-3)(x-1)^3(x+1)^3(x+3)(x^2-3)^4.\

Notes

  1. ^ McQuillan, Dan; Richter, R. Bruce (1992), "On the crossing numbers of certain generalized Petersen graphs", Discrete Mathematics 104 (3): 311–320, doi:10.1016/0012-365X(92)90453-M, MR1171327 .
  2. ^ Royle, G. F016A data
  3. ^ Conder, M. and Dobcsányi, P. "Trivalent Symmetric Graphs Up to 768 Vertices." J. Combin. Math. Combin. Comput. 40, 41-63, 2002.

References

External links


Wikimedia Foundation. 2010.

Look at other dictionaries:

  • Graphe de Möbius-Kantor — Représentation du graphe de Möbius Kantor Nombre de sommets 16 Nombre d arêtes 24 Distribution des degrés 3 régulier …   Wikipédia en Français

  • Möbius configuration — Example of Möbius configuration; the face planes of red tetrahedron are shown on the top of the image; the blue one on the bottom. The vertex coordinates of the red tetrahedron are: (0,0,0),(0,0,1),(0,1,0),(1,0,0). The vertex coordinates of the… …   Wikipedia

  • Levi graph — infobox graph name = Levi graph image caption = The Pappus graph, a Levi graph with 18 vertices formed from the Pappus configuration. Vertices labeled with single letters correspond to points in the configuration; vertices labeled with three… …   Wikipedia

  • Petersen graph — Infobox graph name = Petersen graph image caption = The Petersen graph is most commonly drawn as a pentagon with a pentagram inside, with five spokes. namesake = Julius Petersen vertices = 10 edges = 15 radius = 2 diameter = 2 girth = 5 chromatic …   Wikipedia

  • August Ferdinand Möbius — Infobox Scientist box width = 300px name = August Möbius image size = 300px caption = August Ferdinand Möbius (1790 ndash;1868) birth date = November 17, 1790 birth place = Schulpforta, Saxony Anhalt, Germany death date = September 26, 1868 death …   Wikipedia

  • Cubic graph — Not to be confused with graphs of cubic functions. The Petersen graph is a Cubic graph …   Wikipedia

  • Nauru graph — The Nauru graph is Hamiltonian. Vertices 24 Edges 36 Radius 4 …   Wikipedia

  • Desargues graph — Named after Gérard Desargues Vertices 20 Edges 30 …   Wikipedia

  • Crossing number (graph theory) — A drawing of the Heawood graph with three crossings. This is the minimum number of crossings among all drawings of this graph, so the graph has crossing number cr(G) = 3. In graph theory, the crossing number cr(G) of a graph G is the… …   Wikipedia

  • Bivariegated graph — In graph theory, a mathematical discipline, a bivariegated graph is a graph whose vertex set can be partitioned into two equal parts such that each vertex is adjacent to exactly one vertex from the other set not containing… …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”