Hamming distance

3-bit binary cube for finding Hamming distance	Two example distances: 100->011 has distance 3 (red path); 010->111 has distance 2 (blue path)
4-bit binary tesseract for finding Hamming distance
Two example distances: 0100->1001 has distance 3 (red path); 0110->1110 has distance 1 (blue path)

In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different. Put another way, it measures the minimum number of substitutions required to change one string into the other, or the number of errors that transformed one string into the other.

Examples

The Hamming distance between:

• "toned" and "roses" is 3.
• 1011101 and 1001001 is 2.
• 2173896 and 2233796 is 3.

Special properties

For a fixed length n, the Hamming distance is a metric on the vector space of the words of that length, as it obviously fulfills the conditions of non-negativity, identity of indiscernibles and symmetry, and it can be shown easily by complete induction that it satisfies the triangle inequality as well. The Hamming distance between two words a and b can also be seen as the Hamming weight of a−b for an appropriate choice of the − operator.

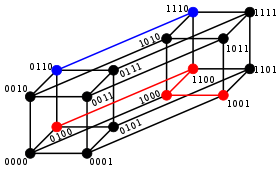
For binary strings a and b the Hamming distance is equal to the number of ones (population count) in a XOR b. The metric space of length-n binary strings, with the Hamming distance, is known as the Hamming cube; it is equivalent as a metric space to the set of distances between vertices in a hypercube graph. One can also view a binary string of length n as a vector in Rⁿ by treating each symbol in the string as a real coordinate; with this embedding, the strings form the vertices of an n-dimensional hypercube, and the Hamming distance of the strings is equivalent to the Manhattan distance between the vertices.

History and applications

The Hamming distance is named after Richard Hamming, who introduced it in his fundamental paper on Hamming codes Error detecting and error correcting codes in 1950.^[1] It is used in telecommunication to count the number of flipped bits in a fixed-length binary word as an estimate of error, and therefore is sometimes called the signal distance. Hamming weight analysis of bits is used in several disciplines including information theory, coding theory, and cryptography. However, for comparing strings of different lengths, or strings where not just substitutions but also insertions or deletions have to be expected, a more sophisticated metric like the Levenshtein distance is more appropriate. For q-ary strings over an alphabet of size q ≥ 2 the Hamming distance is applied in case of orthogonal modulation, while the Lee distance is used for phase modulation. If q = 2 or q = 3 both distances coincide.

The Hamming distance is also used in systematics as a measure of genetic distance.^[2]

On a grid (such as a chessboard), the points at a Lee distance of 1 constitute the von Neumann neighborhood of that point.

Algorithm example

The Python function hamming_distance() computes the Hamming distance between two strings (or other iterable objects) of equal length, by creating a sequence of zero and one values indicating mismatches and matches between corresponding positions in the two inputs, and then summing the sequence.

def hamming_distance(s1, s2):
    assert len(s1) == len(s2)
    return sum(ch1 != ch2 for ch1, ch2 in zip(s1, s2))

The following C function will compute the Hamming distance of two integers (considered as binary values, that is, as sequences of bits). The running time of this procedure is proportional to the Hamming distance rather than to the number of bits in the inputs. It computes the bitwise exclusive or of the two inputs, and then finds the Hamming weight of the result (the number of nonzero bits) using an algorithm of Wegner (1960) that repeatedly finds and clears the lowest-order nonzero bit.

unsigned hamdist(unsigned x, unsigned y)
{
  unsigned dist = 0, val = x ^ y;
 
  // Count the number of set bits
  while(val)
  {
    ++dist; 
    val &= val - 1;
  }
 
  return dist;
}

See also

Mathematics portal

• Damerau–Levenshtein distance
• Euclidean distance
• Jaccard index
• Similarity (mathematics)
• Sørensen similarity index
• Word golf

Notes

1. ^ Hamming (1950).
2. ^ Pilcher, Wong & Pillai (2008).

References

•  This article incorporates public domain material from the General Services Administration document "Federal Standard 1037C".
• Hamming, Richard W. (1950), "Error detecting and error correcting codes", Bell System Technical Journal 29 (2): 147–160, MR0035935, http://www.caip.rutgers.edu/~bushnell/dsdwebsite/hamming.pdf .
• Pilcher, C. D.; Wong, J. K.; Pillai, S. K. (March 2008), "Inferring HIV transmission dynamics from phylogenetic sequence relationships", PLoS Med. 5 (3): e69, doi:10.1371/journal.pmed.0050069, PMC 2267810, PMID 18351799, http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=2267810 .
• Wegner, Peter (1960), "A technique for counting ones in a binary computer", Communications of the ACM 3 (5): 322, doi:10.1145/367236.367286 .

External links

• Hamming Code Tool Tool to generate hamming code
• set_matcher Tool to match two families of sets from the same base population using Hamming distance.