Chiliagon

Regular chiliagon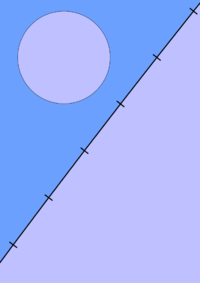
A whole regular chiliagon is not visually discernible from a circle. The lower section is a portion of a regular chiliagon, 200 times larger than the smaller one, with the vertices highlighted.
Edges and vertices	1000
Schläfli symbol	{1000}
Coxeter–Dynkin diagram
Symmetry group	Dihedral (D1000)
Internal angle (degrees)	179.64°
Properties	convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a chiliagon (pronounced /ˈkɪli.əˌgɑn/) is a polygon with 1000 sides.

Properties

The measure of each internal angle in a regular chiliagon is 179.64°. The area of a regular chiliagon with sides of length a is given by

$A = 250a^2 \cot \frac{\pi}{1000} \simeq 79577.2\,a^2$

This result differs from the area of its circumscribed circle by less than 0.0004%.

Because $1000=2^3 \times 5^3$, it is not a product of distinct Fermat primes and a power of two, thus the regular chiliagon it is not a constructible polygon.

Philosophical construction

René Descartes uses the chiliagon as an example in his Sixth meditation to demonstrate the difference between pure intellection and imagination. He says that, when one thinks of a chiliagon, he "does not imagine the thousand sides or see them as if they were present" before him -- as he does when one imagines a triangle, for example. The imagination constructs a "confused representation," which is no different from that which it constructs of a myriagon. However, he does clearly understand what a chiliagon is, just as he understands what a triangle is, and he is able to distinguish it from a myriagon. Therefore, the intellect is not dependent on imagination, Descartes claims, as it is able to entertain clear and distinct ideas when imagination is unable to.^[1]

References

1. ^ Meditation VI by Descartes (English translation).