- Radian
-
For other uses, see Radian (disambiguation).
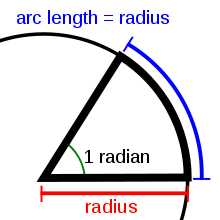
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit. The SI unit of solid angle measurement is the steradian.
The radian is represented by the symbol "rad" or, more rarely, by the superscript c (for "circular measure"). For example, an angle of 1.2 radians would be written as "1.2 rad" or "1.2c" (the second symbol is often mistaken for a degree: "1.2°"). As the ratio of two lengths, the radian is a "pure number" that needs no unit symbol, and in mathematical writing the symbol "rad" is almost always omitted. In the absence of any symbol radians are assumed, and when degrees are meant the symbol ° is used.
Contents
Definition
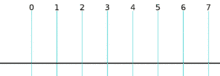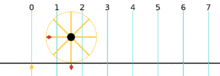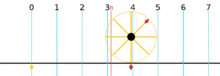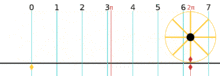
Radian describes the plane angle subtended by a circular arc as the length of the arc divided by the radius of the arc. One radian is the angle subtended at the center of a circle by an arc that is equal in length to the radius of the circle. More generally, the magnitude in radians of such a subtended angle is equal to the ratio of the arc length to the radius of the circle; that is, θ = s /r, where θ is the subtended angle in radians, s is arc length, and r is radius. Conversely, the length of the enclosed arc is equal to the radius multiplied by the magnitude of the angle in radians; that is, s = rθ.
It follows that the magnitude in radians of one complete revolution (360 degrees) is the length of the entire circumference divided by the radius, or 2πr /r, or 2π. Thus 2π radians is equal to 360 degrees, meaning that one radian is equal to 180/π degrees.
History
The concept of radian measure, as opposed to the degree of an angle, is normally credited to Roger Cotes in 1714.[1] He had the radian in everything but name, and he recognized its naturalness as a unit of angular measure. The idea of measuring angles by the length of the arc was used already by other mathematicians. For example al-Kashi (c. 1400) used so-called diameter parts as units where one diameter part was 1/60 radian and they also used sexagesimal subunits of the diameter part.[2]
The term radian first appeared in print on 5 June 1873, in examination questions set by James Thomson (brother of Lord Kelvin) at Queen's College, Belfast. He used the term as early as 1871, while in 1869, Thomas Muir, then of the University of St Andrews, vacillated between rad, radial and radian. In 1874, Muir adopted radian after a consultation with James Thomson.[3][4][5]
Conversions
Conversion between radians and degrees
As stated, one radian is equal to 180/π degrees. Thus, to convert from radians to degrees, multiply by 180/π.
For example:
Conversely, to convert from degrees to radians, multiply by π/180.
For example:

Radians can be converted to turns by dividing the number of radians by 2π.
Radian to degree conversion derivation
We know that the length of circumference of a circle is given by 2πr, where r is the radius of the circle.
So, we can very well say that the following equivalent relation is true:
 [Since a
[Since a  sweep is need to draw a full circle]
sweep is need to draw a full circle]By definition of radian, we can formulate that a full circle represents:
- = 2π rad
Combining both the above relations we can say:
Conversion between radians and grads
2π radians are equal to one turn, which is 400g. So, to convert from radians to grads multiply by 200 / π, and to convert from grads to radians multiply by π / 200. For example,
The table shows the conversion of some common angles.
Units Values Turns 0 





τ Degrees 0° 30° 45° 60° 90° 180° 270° 360° Radians 0 



π 
2π Grads 0g 
50g 
100g 200g 300g 400g Since a turn τ is often identified with the circle constant 2π there is essentially no difference between measuring angles in turns and in radians.
Advantages of measuring in radians
In calculus and most other branches of mathematics beyond practical geometry, angles are universally measured in radians. This is because radians have a mathematical "naturalness" that leads to a more elegant formulation of a number of important results.
Most notably, results in analysis involving trigonometric functions are simple and elegant when the functions' arguments are expressed in radians. For example, the use of radians leads to the simple limit formula
which is the basis of many other identities in mathematics, including
Because of these and other properties, the trigonometric functions appear in solutions to mathematical problems that are not obviously related to the functions' geometrical meanings (for example, the solutions to the differential equation
 , the evaluation of the integral
, the evaluation of the integral  , and so on). In all such cases it is found that the arguments to the functions are most naturally written in the form that corresponds, in geometrical contexts, to the radian measurement of angles.
, and so on). In all such cases it is found that the arguments to the functions are most naturally written in the form that corresponds, in geometrical contexts, to the radian measurement of angles.The trigonometric functions also have simple and elegant series expansions when radians are used; for example, the following Taylor series for sin x :
If x were expressed in degrees then the series would contain messy factors involving powers of π/180: if x is the number of degrees, the number of radians is y = πx /180, so
Mathematically important relationships between the sine and cosine functions and the exponential function (see, for example, Euler's formula) are, again, elegant when the functions' arguments are in radians and messy otherwise.
Dimensional analysis
Although the radian is a unit of measure, it is a dimensionless quantity. This can be seen from the definition given earlier: the angle subtended at the centre of a circle, measured in radians, is equal to the ratio of the length of the enclosed arc to the length of the circle's radius. Since the units of measurement cancel, this ratio is dimensionless.
Another way to see the dimensionlessness of the radian is in the series representations of the trigonometric functions, such as the Taylor series for sin x mentioned earlier:
If x had units, then the sum would be meaningless: the linear term x cannot be added to (or have subtracted) the cubic term x3 / 3! or the quintic term x5 / 5!, etc. Therefore, x must be dimensionless.
Although polar and spherical coordinates use radians to describe coordinates in two and three dimensions, the unit is derived from the radius coordinate, so the angle measure is still dimensionless.[6]
Use in physics
The radian is widely used in physics when angular measurements are required. For example, angular velocity is typically measured in radians per second (rad/s). One revolution per second is equal to 2π radians per second.
Similarly, angular acceleration is often measured in radians per second per second (rad/s2).
For the purpose of dimensional analysis, the units are s−1 and s−2 respectively.
Likewise, the phase difference of two waves can also be measured in radians. For example, if the phase difference of two waves is (k·2π) radians, where k is an integer, they are considered in phase, whilst if the phase difference of two waves is (k·2π + π), where k is an integer, they are considered in antiphase.
Multiples of radian units
Metric prefixes have limited use with radians, and none in mathematics.
There are 2000π milliradians (≈ 6283.185 mrad) in a circle. So a trigonometric milliradian is just under 1⁄6283 of a circle. This “real” trigonometric unit of angular measurement of a circle is in use by telescopic sight manufacturers using (stadiametric) rangefinding in reticles. The divergence of laser beams is also usually measured in milliradians.
An approximation of the trigonometric milliradian (0.001 rad), known as the (angular) mil, is used by NATO and other military organizations in gunnery and targeting. Based upon an approximation of π = 3.2, there are 6400 mils in a circle, so a NATO mil is 1⁄6400 of a circle. Other gunnery systems may use a different approximation to π. Being based on the milliradian, the NATO mil corresponds roughly to an error of 1 m at a range of 1000 m (at such small angles, the curvature is negligible).
Smaller units like microradians (μrads) and nanoradians (nrads) are used in astronomy, and can also be used to measure the beam quality of lasers with ultra-low divergence. Similarly, the prefixes smaller than milli- are potentially useful in measuring extremely small angles.
Criticism
The widespread habit of expressing radians in terms of fractions of π has been criticized because it is like using π as a unit. An angle of π radians represents half a circle, which is a rather arbitrary choice of unit. Various mathematicians and scientists have been critical of the custom of expressing radians as fractions of π, and have proposed using other constants instead. A. Eagle proposed a constant representing one quarter-turn.[7] A constant representing 2π has been proposed because a circle is 2π radians around. Robert Palais proposed to use a "pi with three legs" (
 ) to denote 1 turn,[8] while several people independently have proposed to use the Greek letter τ (tau) instead.[9][10]
) to denote 1 turn,[8] while several people independently have proposed to use the Greek letter τ (tau) instead.[9][10]See also
- Angular mil - military measurement
- Trigonometry
- Harmonic analysis
- Angular frequency
- Grad
- Steradian - the "square radian"
References
- ^ O'Connor, J. J.; Robertson, E. F. (February 2005). "Biography of Roger Cotes". The MacTutor History of Mathematics. http://www-groups.dcs.st-and.ac.uk/~history/Printonly/Cotes.html.
- ^ Luckey, Paul (1953) [Translation of 1424 book]. Siggel, A.. ed. Der Lehrbrief über den kreisumfang von Gamshid b. Mas'ud al-Kasi [Treatise on the Circumference of al-Kashi]. Berlin: Akademie Verlag. pp. 40.
- ^ Cajori, Florian (1929). History of Mathematical Notations. 2. pp. 147–148. ISBN 0486677664.
- ^ Muir, Thos. (1910). "The Term "Radian" in Trigonometry". Nature 83 (2110): 156. doi:10.1038/083156a0.Thomson, James (1910). "The Term "Radian" in Trigonometry". Nature 83 (2112): 217. doi:10.1038/083217c0.Muir, Thos. (1910). "The Term "Radian" in Trigonometry". Nature 83 (2120): 459–460. doi:10.1038/083459d0.
- ^ Miller, Jeff (Nov. 23, 2009). "Earliest Known Uses of Some of the Words of Mathematics". http://jeff560.tripod.com/r.html. Retrieved Sep. 30, 2011.
- ^ For a debate on this meaning and use see: Brownstein, K. R. (1997). "Angles—Let's treat them squarely". American Journal of Physics 65 (7): 605. doi:10.1119/1.18616., Romain, J.E. (1962). "Angles as a fourth fundamental quantity". Journal of Research of the National Bureau of Standards-B. Mathematics and Mathematical Physics 66B (3): 97., LéVy-Leblond, Jean-Marc (1998). "Dimensional angles and universal constants". American Journal of Physics 66 (9): 814. doi:10.1119/1.18964., and Romer, Robert H. (1999). "Units—SI-Only, or Multicultural Diversity?". American Journal of Physics 67: 13. doi:10.1119/1.19185.
- ^ Eagle, Albert (1958). Elliptic Functions as They Should Be: An Account, with Applications, of the Functions in a New Canonical Form. Cambridge: Galloway & Porter. ASIN B0000CK06V.
- ^ Palais, R. (2001). "Pi is Wrong". Mathematical Intelligencer (Springer-Verlag New York) 23 (3): 7–8. doi:10.1007/BF03026846. http://www.math.utah.edu/%7Epalais/pi.pdf.
- ^ Landau, Elizabeth (14 March 2011). "On Pi Day, is 'pi' under attack?". CNN. http://edition.cnn.com/2011/TECH/innovation/03/14/pi.tau.math/. Retrieved 15 March 2011.
- ^ Michael, Hartl (28 June 2010). "The Tau Manifesto". http://tauday.com/. Retrieved 12 January 2011.
External links
SI units Base units 
Derived units Accepted for use
with SIDalton (Atomic mass unit) · Astronomical unit · Day · Decibel · Degree of arc · Electronvolt · Hectare · Hour · Litre · Minute · Minute of arc · Neper · Second of arc · Tonne
Atomic units · Natural unitsSee also SI prefixes · Systems of measurement · Conversion of units · New SI definitions · History of the metric system Book:International System of Units ·
Book:International System of Units ·  Category:SI base unitsCategories:
Category:SI base unitsCategories:- Natural units
- SI derived units
- Trigonometry
- Units of angle
Wikimedia Foundation. 2010.