Phase (waves)

Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.^[1]

Formula

The phase of an oscillation or wave refers to a sinusoidal function such as the following:

$x(t) = A\cdot \cos( 2 \pi f t + \theta )\,$

$y(t) = A\cdot \sin( 2 \pi f t + \theta ) = A\cdot \cos( 2 \pi f t + \theta -\pi/2),\,$

where A, f, and $\scriptstyle \theta$ are constant parameters. These functions are periodic with period $\scriptstyle T = 1/f$, and they are identical except for a displacement of $\scriptstyle T/4$ along the $\scriptstyle t$ axis. The term phase can refer to several different things:

• It can refer to a specified reference, such as $\scriptstyle \cos( 2 \pi f t)\,$, in which case we would say the phase of $\scriptstyle x(t)$ is $\scriptstyle \theta$, and the phase of $\scriptstyle y(t)$ is $\scriptstyle \theta -\pi/2$.
• It can refer to $\scriptstyle \theta$, in which case we would say $\scriptstyle x(t)$ and $\scriptstyle y(t)$ have the same phase but are relative to different references.
• In the context of communication waveforms, the time-variant angle  $\scriptstyle 2 \pi f t + \theta,\,$  or its modulo $\scriptstyle 2\pi$ value, is referred to as instantaneous phase, but often just phase.  Instantaneous phase has a formal definition that is applicable to more general functions and unambiguously defines a function's initial phase at t=0.  Accordingly, it is $\scriptstyle \theta$ for $\scriptstyle x(t)$  and  $\scriptstyle \theta -\pi/2$  for $\scriptstyle y(t)$.  (also see phasor)

Phase shift

Illustration of phase shift. The horizontal axis represents an angle (phase) that is increasing with time.

Phase shift is any change that occurs in the phase of one quantity, or in the phase difference between two or more quantities.^[1]

$\scriptstyle \theta$  is sometimes referred to as a phase-shift, because it represents a "shift" from zero phase. But a change in $\scriptstyle \theta$ is also referred to as a phase shift.

For infinitely long sinusoids, a change in $\scriptstyle \theta$ is the same as a shift in time, such as a time-delay.  If $\scriptstyle x(t)$ is delayed (time-shifted) by  $\scriptstyle \begin{matrix} \frac{1}{4} \end{matrix}$  of its cycle, it becomes:

$x(t - \begin{matrix} \frac{1}{4} \end{matrix}T) \,$	$= A\cdot \cos(2 \pi f (t - \begin{matrix} \frac{1}{4} \end{matrix}T) + \theta) \,$
	$= A\cdot \cos(2 \pi f t - \begin{matrix}\frac{\pi }{2} \end{matrix} + \theta ),\,$

whose "phase" is now $\scriptstyle \theta - \begin{matrix}\frac{\pi }{2} \end{matrix}.$   It has been shifted by $\begin{matrix}\frac{\pi }{2} \end{matrix}$ radians.

Phase difference

In-phase waves

Out-of-phase waves

Left: the real part of a plane wave moving from top to bottom. Right: the same wave after a central section underwent a phase shift, for example, by passing through a glass of different thickness than the other parts. (The illustration on the right ignores the effect of diffraction, which would make the waveform continuous away from material interfaces and would add increasing distortions with distance.).

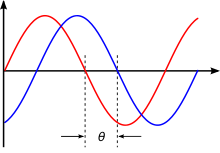
Phase difference is the difference, expressed in electrical degrees or time, between two waves having the same frequency and referenced to the same point in time.^[1] Two oscillators that have the same frequency and different phases have a phase difference, and the oscillators are said to be out of phase with each other. The amount by which such oscillators are out of step with each other can be expressed in degrees from 0° to 360°, or in radians from 0 to 2π. If the phase difference is 180 degrees (π radians), then the two oscillators are said to be in antiphase. If two interacting waves meet at a point where they are in antiphase, then destructive interference will occur. It is common for waves of electromagnetic (light, RF), acoustic (sound) or other energy to become superposed in their transmission medium. When that happens, the phase difference determines whether they reinforce or weaken each other. Complete cancellation is possible for waves with equal amplitudes.

Time is sometimes used (instead of angle) to express position within the cycle of an oscillation.

• A phase difference is analogous to two athletes running around a race track at the same speed and direction but starting at different positions on the track. They pass a point at different instants in time. But the time difference (phase difference) between them is a constant - same for every pass since they are at the same speed and in the same direction. If they were at different speeds (different frequencies), the phase difference is undefined and would only reflect different starting positions. Technically, phase difference between two entities at various frequencies is undefined and does not exist.
• Time zones are also analogous to phase differences.

In-phase and quadrature (I&Q) components

See also: Quadrature phase and Constellation diagram

The term in-phase is also found in the context of communication signals:

$A(t)\cdot \sin[2\pi ft + \phi(t)] = I(t)\cdot \sin(2\pi ft) + Q(t)\cdot \underbrace{\cos(2\pi ft)}_{\sin\left(2\pi ft + \frac{\pi}{2} \right)}$

and:

$A(t)\cdot \cos[2\pi ft + \phi(t)] = I(t)\cdot \cos(2\pi ft) \underbrace{{}- Q(t)\cdot \sin(2\pi ft)}_{{} + Q(t)\cdot \cos\left(2\pi ft + \frac{\pi}{2}\right)},$

where $\ f\,$ represents a carrier frequency, and

$I(t)\ \stackrel{\text{def}}{=}\ A(t)\cdot \cos\left(\phi(t)\right), \,$

$Q(t)\ \stackrel{\text{def}}{=}\ A(t)\cdot \sin\left(\phi(t)\right).\,$

$A(t)\,$ and $\phi(t)\,$ represent possible modulation of a pure carrier wave, e.g.:  $\sin(2\pi ft)\,$ (or $\cos(2\pi ft).\,$) The modulation alters the original $\sin\,$ (or $\cos\,$) component of the carrier, and creates a (new) $\cos\,$ (or $\sin\,$) component, as shown above. The component that is in phase with the original carrier is referred to as the in-phase component. The other component, which is always 90° ($\begin{matrix} \frac{\pi}{2} \end{matrix}$ radians) "out of phase", is referred to as the quadrature component.

Phase coherence

Coherence is the quality of a wave to display well defined phase relationship in different regions of its domain of definition.

In physics, quantum mechanics ascribes waves to physical objects. The wave function is complex and since its square modulus is associated with the probability of observing the object, the complex character of the wave function is associated to the phase. Since the complex algebra is responsible for the striking interference effect of quantum mechanics, phase of particles is therefore ultimately related to their quantum behavior.

Phase compensation

Example of a phase compensation circuit.

Phase compensation is the correction of phase error (i.e., the difference between the actually needed phase and the obtained phase). A phase compensation is required to obtain stability in an opamp. A capacitor/RC network is usually used in the phase compensation to keep a phase margin. A phase compensator subtracts out an amount of phase shift from a signal which is equal to the amount of phase shift added by switching one or more additional amplifier stages into the amplification signal path.

See also

• Instantaneous phase
• Lissajous curve
• Phase angle
• Phase cancellation
• Phase velocity
• Polarity
• Polarization

References

1. ^ ^{a b c} Ballou, Glen (2005). Handbook for sound engineers (3 ed.). Focal Press, Gulf Professional Publishing. p. 1499. ISBN 0240807588. http://books.google.com/books?id=y0d9VA0lkogC&pg=PA1499. 

External links

• Relationship of phase difference and time-delay
• Phase angle, phase difference, time delay, and frequency
• ECE 209: Sources of Phase Shift — Discusses the time-domain sources of phase shift in simple linear time-invariant circuits.
• Phase Difference Java Applet