Sine wave

"Sinusoid" redirects here. For the blood vessel, see Sinusoid (blood vessel).

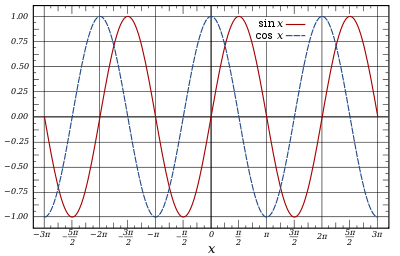The graphs of the sine and cosine functions are sinusoids of different phases.

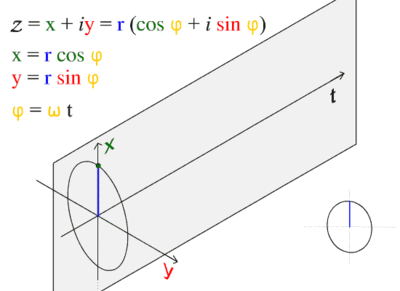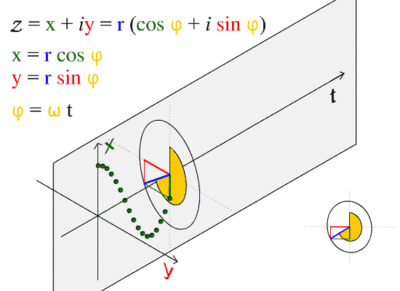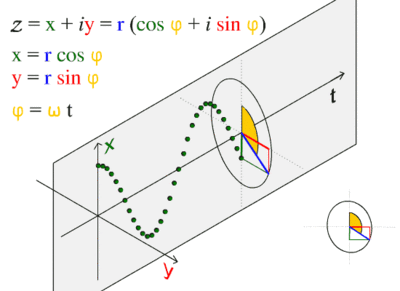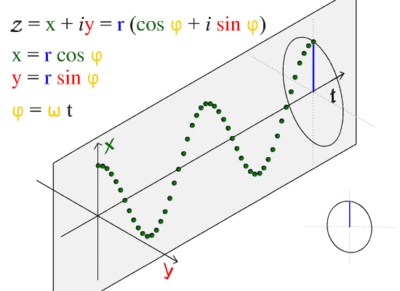
The sine wave or sinusoid is a mathematical function that describes a smooth repetitive oscillation. It occurs often in pure mathematics, as well as physics, signal processing, electrical engineering and many other fields. Its most basic form as a function of time (t) is:

$y(t) = A \cdot \sin(\omega t - \phi)$

where:

• A, the amplitude, is the peak deviation of the function from its center position.
• ω, the angular frequency, specifies how many oscillations occur in a unit time interval, in radians per second
• ɸ, the phase, specifies where in its cycle the oscillation begins at t = 0.
  • When the phase is non-zero, the entire waveform appears to be shifted in time by the amount φ/ω seconds. A negative value represents a delay, and a positive value represents an advance.

The oscillation of an undamped spring-mass system around the equilibrium is a sine wave.

The sine wave is important in physics because it retains its waveshape when added to another sine wave of the same frequency and arbitrary phase. It is the only periodic waveform that has this property. This property leads to its importance in Fourier analysis and makes it acoustically unique.

General form

In general, the function may also have:

• a spatial dimension, x (aka position), with frequency k (also called wavenumber)
• a non-zero center amplitude, D

which looks like this:

$y(x,t) = A\cdot \sin(kx + \omega t- \phi ) + D.\,$

The wavenumber is related to the angular frequency by:.

$k = { \omega \over c } = { 2 \pi f \over c } = { 2 \pi \over \lambda }$

where λ is the wavelength, f is the frequency, and c is the speed of propagation.

This equation gives a sine wave for a single dimension, thus the generalized equation given above gives the amplitude of the wave at a position x at time t along a single line. This could, for example, be considered the value of a wave along a wire.

In two or three spatial dimensions, the same equation describes a travelling plane wave if position x and wavenumber k are interpreted as vectors, and their product as a dot product. For more complex waves such as the height of a water wave in a pond after a stone has been dropped in, more complex equations are needed.

Occurrences

Illustrating the cosine wave's fundamental relationship to the circle.

This wave pattern occurs often in nature, including ocean waves, sound waves, and light waves.

A cosine wave is said to be "sinusoidal", because cos(x) = sin(x + π / 2), which is also a sine wave with a phase-shift of π/2. Because of this "head start", it is often said that the cosine function leads the sine function or the sine lags the cosine.

The human ear can recognize single sine waves as sounding clear because sine waves are representations of a single frequency with no harmonics; some sounds that approximate a pure sine wave are whistling, a crystal glass set to vibrate by running a wet finger around its rim, and the sound made by a tuning fork.

To the human ear, a sound that is made up of more than one sine wave will either sound "noisy" or will have detectable harmonics; this may be described as a different timbre.

Fourier series

Sine, square, triangle, and sawtooth waveforms

Main article: Fourier analysis

In 1822, Joseph Fourier, a French mathematician, discovered that sinusoidal waves can be used as simple building blocks to describe and approximate any periodic waveform including square waves. Fourier used it as an analytical tool in the study of waves and heat flow. It is frequently used in signal processing and the statistical analysis of time series.

See also

• Wave (physics)
• Crest (physics)
• Fourier transform
• Harmonic series (mathematics)
• Harmonic series (music)
• Helmholtz equation
• Instantaneous phase
• Pure tone
• Sawtooth wave
• Sinusoidal model
• Simple harmonic motion
• Square wave
• Triangle wave
• Wave equation

References

• Hazewinkel, Michiel, ed. (2001), "Sinusoid", Encyclopaedia of Mathematics, Springer, ISBN 978-1556080104, http://eom.springer.de/s085640.htm