- Wave equation
-
Not to be confused with Wave function.
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics. Historically, the problem of a vibrating string such as that of a musical instrument was studied by Jean le Rond d'Alembert, Leonhard Euler, Daniel Bernoulli, and Joseph-Louis Lagrange.
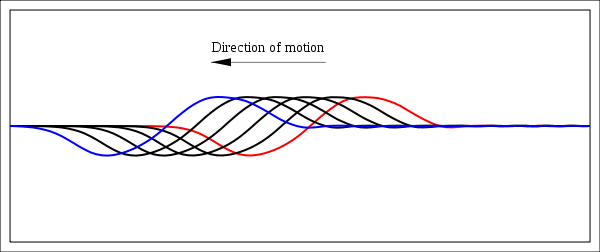
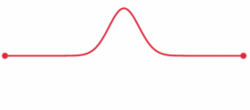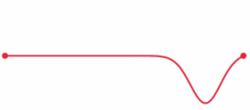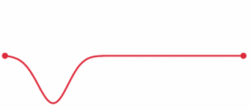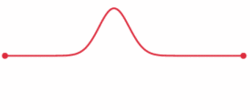 A pulse traveling through a string with fixed endpoints as modeled by the wave equation.
A pulse traveling through a string with fixed endpoints as modeled by the wave equation.
 Spherical waves coming from a point source.
Spherical waves coming from a point source.Introduction
Wave equations are examples of hyperbolic partial differential equations¸ but there are many variations.
In its simplest form, the wave equation concerns a time variable t, one or more spatial variables x1, x2, …, xn, and a scalar function u = u (x1, x2, …, xn; t), whose values could model the height of a wave. The wave equation for u is
where
 is the (spatial) Laplacian and where c is a fixed constant.
is the (spatial) Laplacian and where c is a fixed constant.Solutions of this equation that are initially zero outside some restricted region propagate out from the region at a fixed speed in all spatial directions, as do physical waves from a localized disturbance; the constant c is identified with the propagation speed of the wave. This equation is linear, inasmuch as the sum of any two solutions is again a solution: in physics this property is called the superposition principle.
The equation alone does not specify a solution; a unique solution is usually obtained by setting a problem with further conditions, such as initial conditions, which prescribe the value and velocity of the wave. Another important class of problems specifies boundary conditions, for which the solutions represent standing waves, or harmonics, analogous to the harmonics of musical instruments.
To model dispersive wave phenomena, those in which the speed of wave propagation varies with the frequency of the wave, the constant c is replaced by the phase velocity:
Phenomena in which the speed depends on the amplitude of the wave are modelled by nonlinear wave equations:
A wave may be superimposed onto another movement (for instance sound propagation in a moving medium like a gas flow). In that case the scalar u will contain a Mach factor (which is positive for the wave moving along the flow and negative for the reflected wave).
The elastic wave equation in three dimensions describes the propagation of waves in an isotropic homogeneous elastic medium. Most solid materials are elastic, so this equation describes such phenomena as seismic waves in the Earth and ultrasonic waves used to detect flaws in materials. While linear, this equation has a more complex form than the equations given above, as it must account for both longitudinal and transverse motion:
where:
 and
and  are the so-called Lamé parameters describing the elastic properties of the medium,
are the so-called Lamé parameters describing the elastic properties of the medium, is the density,
is the density, is the source function (driving force),
is the source function (driving force),- and
 is the displacement vector.
is the displacement vector.
Note that in this equation, both force and displacement are vector quantities. Thus, this equation is sometimes known as the vector wave equation.
Variations of the wave equation are also found in quantum mechanics, plasma physics and general relativity.
Scalar wave equation in one space dimension
Derivation of the wave equation
From Hooke's law
The wave equation in the one dimensional case can be derived from Hooke's law in the following way: Imagine an array of little weights of mass m interconnected with massless springs of length h . The springs have a spring constant of k:
Here u(x) measures the distance from the equilibrium of the mass situated at x. The forces exerted on the mass m at the location x + h are:
The equation of motion for the weight at the location x+h is given by equating these two forces:
where the time-dependence of u(x) has been made explicit.
If the array of weights consists of N weights spaced evenly over the length L = N h of total mass M = N m, and the total spring constant of the array K = k/N we can write the above equation as:
Taking the limit
 (and assuming smoothness) one gets:
(and assuming smoothness) one gets:(KL2)/M is the square of the propagation speed in this particular case.
From the generic scalar transport equation
Starting with the generic scalar transport equation without diffusion,
 ,
,
we differentiate with respect to t to get
 .
.
Assuming that
 and u are constant, we may write
and u are constant, we may write .
.
Substituting for the time derivative of
 we get
we get![\frac{\partial^2\phi}{\partial t^2}+u\frac{\partial}{\partial x}\left[S_\phi-\frac{\partial(u\phi)}{\partial x}\right]=\frac{\partial^2\phi}{\partial t^2}-u^2\frac{\partial^2\phi}{\partial x^2}=0](3/933d1c166b0835544f1417c713a45037.png) ,
,
where u is the speed of propagation of the scalar
 which, in general, is a function of time and position.
which, in general, is a function of time and position.General solution
The one dimensional wave equation is unusual for a partial differential equation in that a relatively simple general solution may be found. Defining new variables:[1]
changes the wave equation into
which leads to the general solution
In other words, solutions of the 1D wave equation are sums of a right traveling function F and a left traveling function G. "Traveling" means that the shape of these individual arbitrary functions with respect to x stays constant, however the functions are translated left and right with time at the speed c. This was derived by Jean le Rond d'Alembert.[2]
Another way to arrive at this result is to note that the wave equation may be "factored":
These last two equations are advection equations, one left traveling and one right, both with constant speed c.
For an initial value problem, the arbitrary functions F and G can be determined to satisfy initial conditions:
The result is d'Alembert's formula:
In the classical sense if
 and
and  then
then  . However, the waveforms F and G may also be generalized functions, such as the delta-function. In that case, the solution may be interpreted as an impulse that travels to the right or the left.
. However, the waveforms F and G may also be generalized functions, such as the delta-function. In that case, the solution may be interpreted as an impulse that travels to the right or the left.The basic wave equation is a linear differential equation and so it will adhere to the superposition principle. This means that the net displacement caused by two or more waves is the sum of the displacements which would have been caused by each wave individually. In addition, the behavior of a wave can be analyzed by breaking up the wave into components, e.g. the Fourier transform breaks up a wave into sinusoidal components.
Scalar wave equation in three space dimensions
The solution of the initial-value problem for the wave equation in three space dimensions can be obtained from the solution for a spherical wave. This result can then be used to obtain the solution in two space dimensions.
Spherical waves
The wave equation is unchanged under rotations of the spatial coordinates, and therefore one may expect to find solutions that depend only on the radial distance from a given point. Such solutions must satisfy
This equation may be rewritten as
the quantity ru satisfies the one-dimensional wave equation. Therefore there are solutions in the form
where F and G are arbitrary functions. Each term may be interpreted as a spherical wave that expands or contracts with velocity c. Such waves are generated by a point source, and they make possible sharp signals whose form is altered only by a decrease in amplitude as r increases (see an illustration of a spherical wave on the top right). Such waves exist only in cases of space with odd dimensions.
Monochromatic spherical wave
A point source is vibrating at a single frequency f with phase = 0 at t = 0 with a peak-to-peak magnitude of 2a. A spherical wave is propagated from the point. The phase of the propagated wave changes as kr where r is the distance travelled from the source. The magnitude falls off as 1 / r since the energy falls off as 1 / r2. The complex amplitude of the spherical wave at r is therefore given by: [3]

Solution of a general initial-value problem
The wave equation is linear in u and it is left unaltered by translations in space and time. Therefore we can generate a great variety of solutions by translating and summing spherical waves. Let φ(ξ,η,ζ) be an arbitrary function of three independent variables, and let the spherical wave form F be a delta-function: that is, let F be a weak limit of continuous functions whose integral is unity, but whose support (the region where the function is non-zero) shrinks to the origin. Let a family of spherical waves have center at (ξ,η,ζ), and let r be the radial distance from that point. Thus
If u is a superposition of such waves with weighting function φ, then
the denominator 4πc is a convenience.
From the definition of the delta-function, u may also be written as
where α, β, and γ are coordinates on the unit sphere S, and ω is the area element on S. This result has the interpretation that u(t,x) is t times the mean value of φ on a sphere of radius ct centered at x:
It follows that
The mean value is an even function of t, and hence if
then
These formulas provide the solution for the initial-value problem for the wave equation. They show that the solution at a given point P, given (t,x,y,z) depends only on the data on the sphere of radius ct that is intersected by the light cone drawn backwards from P. It does not depend upon data on the interior of this sphere. Thus the interior of the sphere is a lacuna for the solution. This phenomenon is called Huygens' principle. It is true for odd numbers of space dimension, where for one dimension the integration is performed over the boundary of an interval with respect to the Dirac measure. It is not satisfied in even space dimensions. The phenomenon of lacunas has been extensively investigated in Atiyah, Bott and Gårding (1970, 1973).
Scalar wave equation in two space dimensions
In two space dimensions, the wave equation is
We can use the three-dimensional theory to solve this problem if we regard u as a function in three dimensions that is independent of the third dimension. If
then the three-dimensional solution formula becomes
where α and β are the first two coordinates on the unit sphere, and dω is the area element on the sphere. This integral may be rewritten as an integral over the disc D with center (x,y) and radius ct:
It is apparent that the solution at (t,x,y) depends not only on the data on the light cone where
but also on data that are interior to that cone.
Problems with boundaries
One space dimension
The Sturm-Liouville formulation
A flexible string that is stretched between two points x = 0 and x = L satisfies the wave equation for t > 0 and 0 < x < L. On the boundary points, u may satisfy a variety of boundary conditions. A general form that is appropriate for applications is
where a and b are non-negative. The case where u is required to vanish at an endpoint is the limit of this condition when the respective a or b approaches infinity. The method of separation of variables consists in looking for solutions of this problem in the special form
A consequence is that
The eigenvalue λ must be determined so that there is a non-trivial solution of the boundary-value problem
This is a special case of the general problem of Sturm–Liouville theory. If a and b are positive, the eigenvalues are all positive, and the solutions are trigonometric functions. A solution that satisfies square-integrable initial conditions for u and ut can be obtained from expansion of these functions in the appropriate trigonometric series.
Investigation by numerical methods
Approximating the continuous string with a finite number of equidistant mass points one gets the following physical model:
If each mass point has the mass m, the tension of the string is f, the separation between the mass points is Δx and
 are the offset of these n points from their equilibrium points (i.e. their position on a straight line between the two attachment points of the string) the vertical component of the force towards point i + 1 is
are the offset of these n points from their equilibrium points (i.e. their position on a straight line between the two attachment points of the string) the vertical component of the force towards point i + 1 is
(
and the vertical component of the force towards point i − 1 is

(
Taking the sum of these two forces and dividing with the mass m one gets for the vertical motion:

(
As the mass density is
this can be written

(
The wave equation is obtained by letting
 in which case ui(t) takes the form u(x,t) where u(x,t) is continuous function of two variables,
in which case ui(t) takes the form u(x,t) where u(x,t) is continuous function of two variables,  takes the form
takes the form  and
andBut the discrete formulation (3) of the equation of state with a finite number of mass point is just the suitable one for a numerical propagation of the string motion. The boundary condition
- u(0,t) = u(L,t) = 0
where L is the length of the string takes in the discrete formulation the form that for the outermost points u1 and un the equation of motion are

(
and

(
while for 1 < i < n

(
where

If the string is approximated with 100 discrete mass points one gets the 100 coupled second order differential equations (5), (6) and (7) or equivalently 200 coupled first order differential equations.
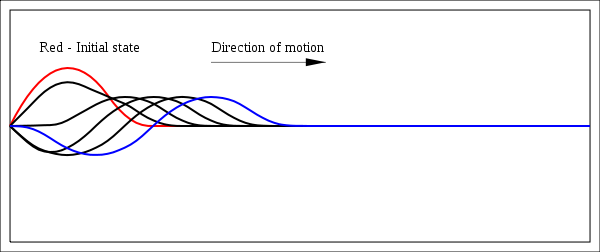
Propagating these up to the timesusing an 8-th order multistep method the 6 states displayed in figure 2 are found:
The red curve is the initial state at time zero at which the string is "let free" in a predefined shape [4] with all . The blue curve is the state at time
. The blue curve is the state at time  , i.e. after a time that corresponds to the time a wave that is moving with the nominal wave velocity
, i.e. after a time that corresponds to the time a wave that is moving with the nominal wave velocity  would need for one fourth of the length of the string.
would need for one fourth of the length of the string.Figure 3 displays the shape of the string at the times
 . The wave travels in direction right with the speed
. The wave travels in direction right with the speed  without being actively constraint by the boundary conditions at the two extrems of the string. The shape of the wave is constant, i.e. the curve is indeed of the form
without being actively constraint by the boundary conditions at the two extrems of the string. The shape of the wave is constant, i.e. the curve is indeed of the formFigure 4 displays the shape of the string at the times
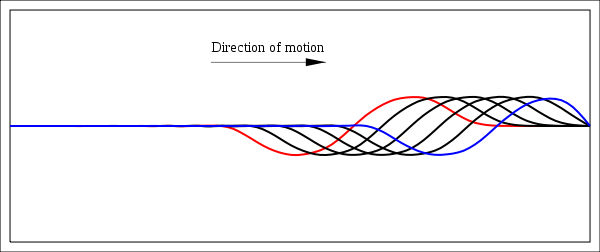
 . The constraint on the right extreme starts to interfere with the motion preventing the wave to raise the end of the string.
. The constraint on the right extreme starts to interfere with the motion preventing the wave to raise the end of the string.Figure 5 displays the shape of the string at the times
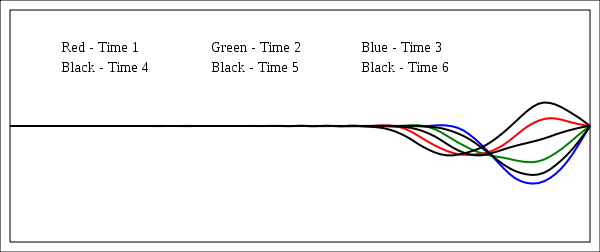
 when the direction of motion is reversed. The red, green and blue curves are the states at the times
when the direction of motion is reversed. The red, green and blue curves are the states at the times  while the 3 black curves correspond to the states at times
while the 3 black curves correspond to the states at times  with the wave starting to move back towards left.
with the wave starting to move back towards left.
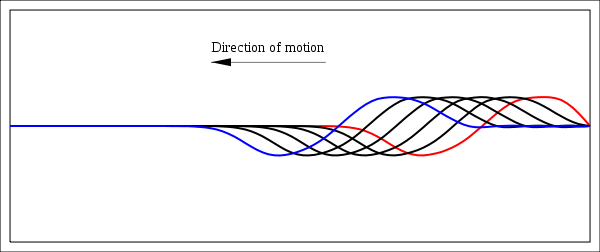
Figure 6 and figure 7 finally display the shape of the string at the times and
and  . The wave now travels towards left and the constraints at the end points are not active any more. When finally the other extreme of the string the direction will again be reversed in a way similar to what is displayed in figure 6
. The wave now travels towards left and the constraints at the end points are not active any more. When finally the other extreme of the string the direction will again be reversed in a way similar to what is displayed in figure 6Several space dimensions
The one-dimensional initial-boundary value theory may be extended to an arbitrary number of space dimensions. Consider a domain D in m-dimensional x space, with boundary B. Then the wave equation is to be satisfied if x is in D and t > 0. On the boundary of D, the solution u shall satisfy
where n is the unit outward normal to B, and a is a non-negative function defined on B. The case where u vanishes on B is a limiting case for a approaching infinity. The initial conditions are
where f and g are defined in D. This problem may be solved by expanding f and g in the eigenfunctions of the Laplacian in D, which satisfy the boundary conditions. Thus the eigenfunction v satisfies
in D, and
on B.
In the case of two space dimensions, the eigenfunctions may be interpreted as the modes of vibration of a drumhead stretched over the boundary B. If B is a circle, then these eigenfunctions have an angular component that is a trigonometric function of the polar angle θ, multiplied by a Bessel function (of integer order) of the radial component. Further details are in Helmholtz equation.
If the boundary is a sphere in three space dimensions, the angular components of the eigenfunctions are spherical harmonics, and the radial components are Bessel functions of half-integer order.
Inhomogeneous wave equation in one dimension
The inhomogeneous wave equation in one dimension is the following:
with initial conditions given by
The function s(x,t) is often called the source function because in practice it describes the effects of the sources of waves on the medium carrying them. Physical examples of source functions include the force driving a wave on a string, or the charge or current density in the Lorenz gauge of electromagnetism.
One method to solve the initial value problem (with the initial values as posed above) is to take advantage of the property of the wave equation that its solutions obey causality. That is, for any point (xi,ti), the value of
 depends only on the values of
depends only on the values of  and
and  and the values of the function
and the values of the function  between
between  and
and  . This can be seen in d'Alembert's formula, stated above, where these quantities are the only ones that show up in it. Physically, if the maximum propagation speed is
. This can be seen in d'Alembert's formula, stated above, where these quantities are the only ones that show up in it. Physically, if the maximum propagation speed is  , then no part of the wave that can't propagate to a given point by a given time can affect the amplitude at the same point and time.
, then no part of the wave that can't propagate to a given point by a given time can affect the amplitude at the same point and time.In terms of finding a solution, this causality property means that for any given point on the line being considered, the only area that needs to be considered is the area encompassing all the points that could causally affect the point being considered. Denote the area that casually affects point
 as
as  . Suppose we integrate the inhomogeneous wave equation over this region.
. Suppose we integrate the inhomogeneous wave equation over this region.To simplify this greatly, we can use Green's theorem to simplify the left side to get the following:
The left side is now the sum of three line integrals along the bounds of the causality region. These turn out to be fairly easy to compute
In the above, the term to be integrated with respect to time disappears because the time interval involved is zero, thus dt = 0.
For the other two sides of the region, it is worth noting that
 is a constant, namingly
is a constant, namingly  , where the sign is chosen appropriately. Using this, we can get the relation
, where the sign is chosen appropriately. Using this, we can get the relation  , again choosing the right sign:
, again choosing the right sign:And similarly for the final boundary segment:
Adding the three results together and putting them back in the original integral:
In the last equation of the sequence, the bounds of the integral over the source function have been made explicit. Looking at this solution, which is valid for all choices (xi,ti) compatible with the wave equation, it is clear that the first two terms are simply d'Alembert's formula, as stated above as the solution of the homogeneous wave equation in one dimension. The difference is in the third term, the integral over the source.
Other coordinate systems
In three dimensions, the wave equation, when written in elliptic cylindrical coordinates, may be solved by separation of variables, leading to the Mathieu differential equation.
See also
- Acoustic wave equation
- Electromagnetic wave equation
- Helmholtz equation
- Inhomogeneous electromagnetic wave equation
- Laplace operator
- Schrödinger equation
- Standing wave
- Vibrations of a circular drum
- Bateman transform
- Maxwell's equations
- Wheeler-Feynman absorber theory
Notes and references
Notes
- ^ Eric W. Weisstein. "d'Alembert's Solution". MathWorld. http://mathworld.wolfram.com/dAlembertsSolution.html. Retrieved 2009-01-21.
- ^ D'Alembert (1747) "Recherches sur la courbe que forme une corde tenduë mise en vibration" (Researches on the curve that a tense cord forms [when] set into vibration), Histoire de l'académie royale des sciences et belles lettres de Berlin, vol. 3, pages 214-219. See also: D'Alembert (1747) "Suite des recherches sur la courbe que forme une corde tenduë mise en vibration" (Further researches on the curve that a tense cord forms [when] set into vibration), Histoire de l'académie royale des sciences et belles lettres de Berlin, vol. 3, pages 220-249. See also: D'Alembert (1750) "Addition au mémoire sur la courbe que forme une corde tenduë mise en vibration," Histoire de l'académie royale des sciences et belles lettres de Berlin, vol. 6, pages 355-360.
- ^ RS Longhurst, Geometrical and Physical Optics, 1967, Longmans, Norwich
- ^ The initial state for "Investigation by numerical methods" is set with quadratic splines as follows:
 for
for 
 for
for 
- u(0,x) = 0 for


References
- M. F. Atiyah, R. Bott, L. Garding, "Lacunas for hyperbolic differential operators with constant coefficients I", Acta Math., 124 (1970), 109–189.
- M.F. Atiyah, R. Bott, and L. Garding, "Lacunas for hyperbolic differential operators with constant coefficients II", Acta Math., 131 (1973), 145–206.
- R. Courant, D. Hilbert, Methods of Mathematical Physics, vol II. Interscience (Wiley) New York, 1962.
- "Linear Wave Equations", EqWorld: The World of Mathematical Equations.
- "Nonlinear Wave Equations", EqWorld: The World of Mathematical Equations.
- William C. Lane, "MISN-0-201 The Wave Equation and Its Solutions", Project PHYSNET.
External links
- Nonlinear Wave Equations by Stephen Wolfram and Rob Knapp and Nonlinear Wave Equation Explorer by Stephen Wolfram, and Wolfram Demonstrations Project.
- Mathematical aspects of wave equations are discussed on the Dispersive PDE Wiki.
Categories:- Fundamental physics concepts
- Hyperbolic partial differential equations
- Wave mechanics
Wikimedia Foundation. 2010.







![F_\mathit{Hooke} = F_{x+2h} + F_x = k \left [ {u(x+2h,t) - u(x+h,t)} \right ] + k[u(x,t) - u(x+h,t)]](6/236e998a4c1886befc437a9146805f2b.png)
![m{\partial^2u(x+h,t) \over \partial t^2}= k[u(x+2h,t)-u(x+h,t)-u(x+h,t)+u(x,t)]](6/4b6e13f0f6afda0c53a6dae55607cb40.png)
![{\partial^2u(x+h,t) \over \partial t^2}={KL^2 \over M}{[u(x+2h,t)-2u(x+h,t)+u(x,t)] \over h^2}](b/c4b9ce1b739ab097275e24cb7f5e06d3.png)




![\left[\frac{\part}{\part t} - c\frac{\part}{\part x}\right] \left[ \frac{\part}{\part t} + c\frac{\part}{\part x}\right] u = 0](2/a820aa87a1928fe1dc21446a0c5f3adb.png)











![u(t,x,y,z) = t M_{ct}[\phi]. \,](0/d301d237a9ef372ce472af3f24da3141.png)

![v(t,x,y,z) = \frac{\part}{\part t} \left( t M_{ct}[\psi] \right), \,](e/6aedb0cc8f27d5f913cfc33f43f91968.png)



![u(t,x,y) = tM_{ct}[\phi] = \frac{t}{4\pi} \iint_S \phi(x + ct\alpha,\, y + ct\beta) d\omega,\,](2/8c2795ac222ed83a4fab709b31a952b9.png)