- Turn (geometry)
-
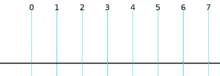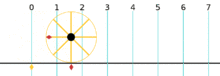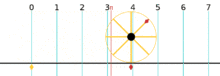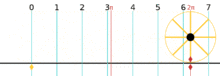
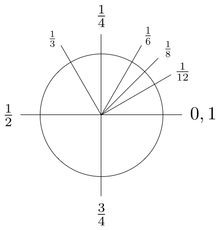 Rotations about the center point where a complete rotation is equal to 1 turn
Rotations about the center point where a complete rotation is equal to 1 turn
A turn is an angle equal to a 360° or 2π radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot.
A turn can be subdivided in many different ways, into half turns, quarter turns, centiturns, milliturns, binary angles, points etc.
Contents
Subdivision of turns
A turn can be divided in 100 centiturns or 1000 milliturns with each milliturn corresponding to an angle of 0.36°, which can also be written as 21'36".
Binary fractions of a turn are also used. Sailors have traditionally divided a turn into 32 points. The binary degree, also known as the binary radian (or brad), is 1/256 turn.[1] The binary degree is used in computing so that an angle can be efficiently represented in a single byte (albeit to limited precision). Other measures of angle used in computing may be based on dividing one whole turn into 2n equal parts for other values of n.[2]
The notion of turn is commonly used for planar rotations. Two special rotations have acquired appellations of their own: a rotation through 180° is commonly referred to as a half-turn (π radians),[3] a rotation through 90° is referred to as a quarter-turn. A half-turn is often referred to as a reflection in a point since these are identical for transformations in two-dimensions.
History
The word turn originates via Latin and French from the Greek word τόρνος (tornos – a lathe).
The geometric notion of a turn has its origin in the sailors terminology of knots where a turn means one round of rope on a pin or cleat, or one round of a coil.[4] For knots the English terms of single turn, round turn and double round turn do not translate directly into the geometric notion of turn, but in German the correspondence is exact.[5]
In 1697 David Gregory used π / ρ (pi/rho) to denote the perimeter of a circle (i.e. the circumference) divided by its radius,[6][7] though δ / π (delta/pi) had been used by William Oughtred in 1647 for the ratio of diameter to perimeter. The first use of π on its own with its present meaning of perimeter/diameter was by William Jones in 1706.[8] Euler adopted the symbol with that meaning in 1737, leading to its widespread use.
The idea of using centiturns and milliturns as units was introduced by Sir Fred Hoyle.[9]
Robert Palais proposed in 2001 to use the number of radians in a turn as the fundamental circle constant instead of π, in order to make mathematics simpler and more intuitive, using a "pi with three legs" symbol to denote 1 turn (
 ).[10] In 2010, Michael Hartl proposed to use the Greek letter τ (tau) to represent the number 2π instead.[11][12][13][14]
).[10] In 2010, Michael Hartl proposed to use the Greek letter τ (tau) to represent the number 2π instead.[11][12][13][14]Mathematical constants
One turn can be identified with 2π (≈6.28)[15] radians.
Similarly, half a turn is often identified with the mathematical constant π because half a turn is π (≈3.14)[16] radians.
Conversion of some common angles
Units Values Turns 0 1/12 1/10 1/8 1/6 1/5 1/4 1/2 3/4 1 Radians 0 








Degrees 0° 30° 36° 45° 60° 72° 90° 180° 270° 360° Grads 0g 33⅓g 40g 50g 66⅔g 80g 100g 200g 300g 400g Examples of use
- As an angular unit it is particularly useful for large angles, such as in connection with coils and rotating objects. See also winding number.
- Turn is used in complex dynamics for measure of external and internal angles. The sum of external angles of a polygon equals one turn.
- Pie charts illustrate proportions of a whole as fractions of a turn. Each one percent is shown as an angle of one centiturn.
Kinematics of turns
In kinematics a turn is a rotation less than a full revolution. A turn may be represented in a mathematical model that uses expressions of complex numbers or quaternions. In the complex plane every non-zero number has a polar coordinate expression z = r cos a + r i sin a where r > 0 and a is in [0, 2π). A turn of the complex plane arises from multiplying z = x + i y by an element u = eb i that lies on the unit circle:
Frank Morley consistently referred to elements of the unit circle as turns in the book Inversive Geomety (1933) that he coauthored with his son Frank Vigor Morley.
The Latin term for turn is versor, which is a quaternion that can be visualized as an arc of a great circle. The product of two versors can be compared to a spherical triangle where two sides add to the third. For the kinematics of rotation in three dimensions, see quaternions and spatial rotation.
See also
- Revolutions per minute
- Angle of rotation
Notes and References
- ^ ooPIC Programmer's Guide www.oopic.com
- ^ Angles, integers, and modulo arithmetic Shawn Hargreaves blogs.msdn.com
- ^ Half Turn, Reflection in Point cut-the-knot.org
- ^ Ashley, C. The Ashley Book of Knots, New York 1944. p. 604.
- ^ Harremoes, Peter (21 February 2011), Gregory's constant Tau, http://www.harremoes.dk/Peter/Undervis/Turnpage/Turnpage1.html
- ^ Beckmann, P., A History of Pi. Barnes & Noble Publishing, 1989.
- ^ Schwartzman, S., The Words of Mathematics. The Mathematical Association of America,1994. Page 165
- ^ Pi through the ages
- ^ Hoyle, F., Astronomy. London, 1962.
- ^ Palais, R. 2001: Pi is Wrong, The Mathematical Intelligencer. Springer-Verlag New York. Volume 23, Number 3, pp. 7–8
- ^ No, really, pi is wrong: The Tau Manifesto – Michael Hartl
- ^ Michael Hartl (June 28, 2010). "The Tau Manifesto". http://tauday.com/. Retrieved January 12, 2011.
- ^ Aron, Jacob (8 January 2011), "Interview: Michael Hartl: It's time to kill off pi", New Scientist 209 (2794), doi:10.1016/S0262-4079(11)60036-5
- ^ Landau, Elizabeth (14 March 2011), "On Pi Day, is 'pi' under attack?", cnn.com, http://edition.cnn.com/2011/TECH/innovation/03/14/pi.tau.math/index.html
- ^ Sequence
 A019692 in the OEIS.
A019692 in the OEIS. - ^ Sequence
 A000796 in the OEIS.
A000796 in the OEIS.
Further reading
- Aron, Jacob (8 January 2011), "Interview: Michael Hartl: It's time to kill off pi", New Scientist 209 (2794), doi:10.1016/S0262-4079(11)60036-5
- Landau, Elizabeth (14 March 2011), "On Pi Day, is 'pi' under attack?", cnn.com, http://edition.cnn.com/2011/TECH/innovation/03/14/pi.tau.math/index.html
External links
Categories:- Units of angle
Wikimedia Foundation. 2010.