- Tau (2π)
-
Part of a series of articles on the mathematical constant π 
Uses Area of disk · Circumference
Use in other formulaeProperties Irrationality · Transcendence
Less than 22/7Value Approximations · Memorization People Archimedes · Liu Hui · Zu Chongzhi
Madhava of Sangamagrama
William Jones · John Machin
John Wrench · Ludolph van CeulenHistory Chronology · Book In culture Legislation · Holiday Related topics Squaring the circle · Basel problem
Tau (τ) · Other topics related to πTau (τ) is a mathematical constant equal to the ratio of any circle's circumference to its radius, a value of approximately 6.28318531. It was introduced as an alternative to pi (π), which equals the ratio of circumference to diameter. Angles are measured in radians, and a circle is usually defined as all points in a plane a certain distance — the radius — away from a center point. So radius is often considered more fundamental to circles than diameter. Proponents of tau claim this naturally leads the mathematics to be clearer, more consistent, and easier to learn using tau (circumference divided by radius) instead of pi (circumference divided by diameter).
Tau (τ) has been proposed by Bob Palais, Peter Harremoes, Michael Hartl, and others, as a replacement for the current circle constant, π.[1][2][3][4]
Circles are more naturally defined by their radius than by their diameter.[note 1]
The value τ = 2π occurs very frequently in mathematics, another reason it is suggested as a replacement for π.
Proponents of τ say π makes mathematics harder for students to learn, without the added benefits they would get if they could instead apply that extra time and effort to learning more advanced mathematics.[citation needed]
Contents
Geometry
Angles and radians
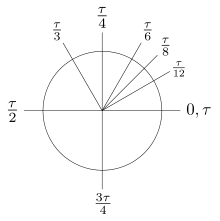
- One radian, the fundamental unit of angle measurement, is the angle a one-radius-length arc subtends on a circle. So the number of radians in a full circle equals the number of one-radius-length arcs around a circle, which is the ratio of a circle's circumference to its radius. This is the definition of τ.
- Since τ radians covers a full circle, 1 2 τ radians covers 1 2 a circle, 3 4 τ radians covers 3 4 a circle, and so on. Converting in the opposite direction, 1 2 a circle has an angle measuring 1 2 τ radians, 3 4 a circle has an angle measuring 3 4 τ radians, and so on. So the fraction does not change when converting in either direction.
- By comparison, 1 2 π radians covers 1 4 a circle, 3 4 π radians covers 3 8 a circle, and so on. Converting in the opposite direction, 1 2 a circle has an angle measuring 2 2 π = π radians, 3 4 a circle has an angle measuring 6 4 π = 3 2 π radians, and so on. With π, the fraction does change, either multiplying or dividing by 2, depending on the direction of conversion. So using π instead of τ imposes two extra steps, first deciding whether the fraction must be multiplied or divided by 2, then actually doing the multiplication or division.
- The so-called "special angles" that need to be memorized when using π simply become fractions of a whole circle when using τ, e.g.
 ,
,  ,
,  ,
,  and
and  . It is easier to explain that one eighth of a circle corresponds to
. It is easier to explain that one eighth of a circle corresponds to  radians than to
radians than to  radians.[5] Hartl describes the use of π in this context as a "pedagogical disaster".
radians.[5] Hartl describes the use of π in this context as a "pedagogical disaster".
Circles, arcs and sectors
- The circle circumference formula 2πr simplifies to τr.
- The circle area formula πr2 becomes the more complex
 .
. - With τ, both the circumference and area formulas for a circle have forms identical to the arclength (θr) and area
 formulas for a circular sector; with π, neither formula does. A whole circle is just a circle sector with θ = τ, so students could memorize just two formulas instead of four.[6]
formulas for a circular sector; with π, neither formula does. A whole circle is just a circle sector with θ = τ, so students could memorize just two formulas instead of four.[6] - The base
 and area
and area  formulas for a skinny triangle also have those forms. They can be used to derive the
formulas for a skinny triangle also have those forms. They can be used to derive the  or
or  formula pairs above by cutting a sector or circle into many pizza-style slices and approximating those slices as skinny triangles. The sum of the triangles' vertex angles
formula pairs above by cutting a sector or circle into many pizza-style slices and approximating those slices as skinny triangles. The sum of the triangles' vertex angles  equals
equals  or
or  so the sum of their bases
so the sum of their bases  equals
equals  or
or  and the sum of their areas
and the sum of their areas  equals
equals  or
or  [6]
[6]


circumference and area of a circle. 

arclength and area of a circular sector. 

base and area of a skinny triangle. In physics there are many other examples of this pattern of two important formulas, (1) a constant times a variable, and (2) its integral which is  times the constant times the variable squared. [2]
times the constant times the variable squared. [2]

velocity and displacement after constant acceleration (starting from rest) 

angular velocity and angular displacement after constant angular acceleration (starting from rest) 

momentum and kinetic energy 

angular momentum and rotational energy 

spring force applied and spring potential energy 

torque applied and torsion pendulum potential energy 

electric flux density and electric field energy density 

capacitor charge and energy stored 

magnetic flux density and magnetic field energy density 

inductor flux and energy stored Straight lines and polygons
- A straight angle (or the sum of the angles in a linear pair[note 2]) describes the angle on only one side of a line, which is π. The total angle measure on both sides of that line is τ = π + π.
- When a transversal intersects two parallel lines, the sum of the interior angles on only one side of the transversal is π. The sum of the interior angles on both sides of the transversal is τ = π + π.[citation needed]
- The sum of the exterior angles of a polygon is τ.
- The sum of the interior angles of a triangle is π. More generally, the sum of the interior angles of a simple n-gon is (n − 2)π. [7]
- Each (additional) vertex added to a simple polygon increases its total angle sum by τ. The increase is always divided equally between the internal and outside angle sums. (outside angle = τ − internal angle and is not the same as external angle)
-
- Sum of internal angles = nτ 2 − τ Sum of outside angles = nτ 2 + τ Sum of internal angles + Sum of outside angles = nτ
- Area of a regular n-sided polygon inscribed in the unit circle

Trigonometry and complex numbers
Functions based on the unit circle
- The unit circle's circumference is τ, but its area is π. τ proponents argue that the unit circle's circumference is the more important quantity because it becomes the period of the ubiquitous sine, cosine, and complex exponential functions, while π advocates argue that the use of π for the area of the unit circle is more elegant.[7]
- The periodicity of the cosine, sine, and complex exponential
 functions is τ instead of 2π, which is simpler and arguably more intuitive.[4]
functions is τ instead of 2π, which is simpler and arguably more intuitive.[4] - The nth roots of unity
 where k = 0,..,n-1.
where k = 0,..,n-1. - Cauchy's integral formula

Euler's Identity

When Euler's Identity is written  , it provides the value of the complex exponential of the circle constant. So if tau, not pi, is used, then the name Euler's Identity could apply to the even simpler formula
, it provides the value of the complex exponential of the circle constant. So if tau, not pi, is used, then the name Euler's Identity could apply to the even simpler formula  .[2] Although
.[2] Although  shows the complex exponential is periodic with period τ,
shows the complex exponential is periodic with period τ,  does show more—that the complex exponential is antiperiodic with antiperiod π[7] (which also logically implies it is periodic with period 2π = τ).
does show more—that the complex exponential is antiperiodic with antiperiod π[7] (which also logically implies it is periodic with period 2π = τ).
The sum of the nth roots of unity is zero  for n ≥ 2. The n = 2 case of this identity
for n ≥ 2. The n = 2 case of this identity  is just Euler's Identity, but with 2π/2 instead of π
is just Euler's Identity, but with 2π/2 instead of π  . Tau replaces 2π to produce
. Tau replaces 2π to produce  which, unlike
which, unlike  , contains the number 2.[6] In "π is Wrong!", Bob Palais defended this as adding "one more fundamental constant" to Euler's Identity (though he endorsed eiτ = 1 as well).
, contains the number 2.[6] In "π is Wrong!", Bob Palais defended this as adding "one more fundamental constant" to Euler's Identity (though he endorsed eiτ = 1 as well).
The sum of the complex conjugates of the nth roots of unity is also zero for n ≥ 2. Similar analysis to that above produces the identity  . It has all four basic arithmetic operations in "standard" order
. It has all four basic arithmetic operations in "standard" order  ; the numbers
; the numbers  in order; and
in order; and  in alphabetical order.[6] As with the changes to Euler's Identity, these issues are not very (and some not at all) important mathematically. But many people have said they dislike tau because they are fond of Euler's Identity (as currently written with pi) for similar reasons. Therefore they may have a non-trivial effect on whether tau replaces pi.
in alphabetical order.[6] As with the changes to Euler's Identity, these issues are not very (and some not at all) important mathematically. But many people have said they dislike tau because they are fond of Euler's Identity (as currently written with pi) for similar reasons. Therefore they may have a non-trivial effect on whether tau replaces pi.Waves, angular frequency, and the Fourier transform
- Wavenumber

- Angular frequency

- Frequencies may be more recognisable in the (most common time-periodic) functions sin ωt, cos ωt, and eiωt.
-
- For example sin (876.89 τ t) is immediately recognizable as an 876.89 Hz sine wave while sin (1753.78 π t) is not.
- For sums of harmonic terms (like Fourier series), identifying which term is the 6th harmonic is quicker and less error-prone when they're written
 instead of
instead of  .
.
- Reduced Planck constant

- Inductor impedance
 (where
(where  represents the imaginary unit usually represented by
represents the imaginary unit usually represented by  )
) - Capacitor impedance

Fourier transform, using ordinary frequency
- Fourier transform

- Inverse Fourier transform

Common Fourier Transform Pairs Containing 2π = τ 











Fourier transform, using angular frequency, unitary
- Fourier transform

- Inverse Fourier transform

Fourier transform, using angular frequency, non-unitary
- Fourier transform
 (NO CHANGE WITH TAU)
(NO CHANGE WITH TAU) - Inverse Fourier transform

In Other Areas of Mathematics
- Gaussian distribution
- Stirling's approximation

- 2π theorem
- The famous Feynman point (six consecutive 9s early in the decimal digits of π) appears one digit earlier in τ, and is seven digits long instead of six (3.14...349999998... * 2 = 6.28...699999996...).[3][8]
History
Distant Past
- Islamic mathematicians like al-Kashi (c. 1380-1429) focused on the circle constant 6.283... although they were fully aware of the work of Archimedes focusing on the circle constant that is nowadays called π.[3]
- William Jones
- Leonhard Euler
- David Gregory
- Paul Matthieu Hermann Laurent
- Fred Hoyle
Recent
- Following the tradition of Pi Day (March 14, or 3.14), "2pi day" has been celebrated[9][10][11] on June 28 (6.28), and became more widely adopted (as "tau day") since the publication of Hartl's manifesto in 2010. It has been argued that this is a "perfect day" because 6 and 28 are the two first perfect numbers.[2][12][13]
Choice of a symbol
Many symbols have been suggested for the proposed circle constant, including:
- 2π as a single symbol, by Laurent in Traité D'Algebra[1]
 ("pi with 3 legs"), by Palais
("pi with 3 legs"), by Palais (variant pi), by Harremoes
(variant pi), by Harremoes- τ, by Hartl (to stand for turn or τόρνος (tornos), since τ radians are equivalent to one full turn).
Hartl's tau has become the most popular choice for the constant, but opponents argue that the letter τ has many other unrelated mathematical meanings. Supporters on the other hand state that precisely the fact that several meanings already coexist suggests that this is not problematic.
Notes
- ^ For example: x = r cost and y = r sint, or r2 = x2 + y2
- ^ Linear pairs are supplementary, which means that the sum of the angles of a linear pair is 180 degrees, or π radians.
References
- ^ a b Palais, Robert. "Pi is Wrong!". http://www.math.utah.edu/~palais/pi.html. Retrieved 15 March 2011.
- ^ a b c d Michael Hartl. "The Tau Manifesto". http://tauday.com/. Retrieved 9 July 2011.
- ^ a b c Harremoes, Peter. "Al-Kashi's constant τ". http://www.harremoes.dk/Peter/Undervis/Turnpage/Turnpage1.html. Retrieved 9 July 2011.
- ^ a b Palais, Robert (2001). "π Is Wrong!". The Mathematical Intelligencer 23 (3): 7–8. http://www.math.utah.edu/%7Epalais/pi.pdf. Retrieved 2011-07-03.
- ^ Wolchover, Natalie (29 June 2011). "Mathematicians Want to Say Goodbye to Pi". Life's Little Mysteries. http://www.lifeslittlemysteries.com/is-pi-wrong-tau-1815/. Retrieved 2011-07-03.
- ^ a b c d Lindenberg, Joseph. "Tau Before It Was Cool". http://sites.google.com/site/taubeforeitwascool. Retrieved 16 September 2011.
- ^ a b c Cavers, Michael (4 July 2011). "The Pi Manifesto". http://thepimanifesto.com. Retrieved 2011-09-04.
- ^ Michael Hartl. "100,000 digits of τ". http://tauday.com/tau_digits. Retrieved 6 July 2011.
- ^ Lance Fortnow and William Gasarch (1 July 2009). "2pi-day? Other holiday possibilities!". Computational Complexity. http://blog.computationalcomplexity.org/2009/07/2pi-day-other-holiday-possibilities.html. Retrieved 2011-07-24.
- ^ Mathematics (28 June 2009). "2pi Day". Facebook. https://www.facebook.com/event.php?eid=81452665030. Retrieved 2011-07-24.
- ^ Gerald Thurman (author) (6 July 2009) (flv). Eating Pie in Pie Town on Two Pi Day (YouTube). http://www.youtube.com/watch?v=D6eBcvFHECA.
- ^ Marcus du Sautoy (1 July 2009). "Perfect Numbers". The Times. Archived from the original on 2011-08-12. http://www.webcitation.org/60sUl6tNN. Retrieved 2011-08-12.
- ^ Dave Richeson (1 July 2009). "Last Sunday was a perfect day". Division by Zero. http://divisbyzero.com/2009/07/01/last-sunday-was-a-perfect-day/. Retrieved 2011-07-24.
External links
- Vi Hart (Author) (14 March 2011) (flv). Pi Is (still) Wrong (YouTube). http://www.youtube.com/watch?v=jG7vhMMXagQ.
- Kevin Houston (26 June 2011) (flv). Pi is wrong! Here comes Tau Day (YouTube). http://www.youtube.com/watch?v=IF1zcRoOVN0.
- Robert Dixon (Author) (18 June 2011) (flv). Pi ain't all that (YouTube). http://www.youtube.com/watch?v=zC_HGbCCBSI.
- Khan Academy (Salman Khan) (11 July 2011) (flv). Tau versus Pi (YouTube). https://www.youtube.com/watch?v=1jDDfkKKgmc.
 A019692 Decimal expansion of 2*Pi and related links at the On-Line Encyclopedia of Integer Sequences
A019692 Decimal expansion of 2*Pi and related links at the On-Line Encyclopedia of Integer Sequences- "On National Tau Day, Pi Under Attack". Fox News Channel. NewsCore. June 28, 2011. http://www.foxnews.com/scitech/2011/06/28/on-national-tau-day-pi-under-attack/. Retrieved 2011-07-03.
- Springmann, Alessondra (June 28, 2011). "Tau Day: An Even More Fundamental Holiday Than Pi Day". PC World. http://www.pcworld.com/article/231356/tau_day_an_even_more_fundamental_holiday_than_pi_day.html. Retrieved 2011-07-03.
- Palmer, Jason (28 June 2011). "'Tau day' marked by opponents of maths constant pi". BBC News. http://www.bbc.co.uk/news/science-environment-13906169. Retrieved 2011-07-03.
Categories:
Wikimedia Foundation. 2010.