Approximations of π

Timeline of approximations for pi

Part of a series of articles on
the mathematical constant π
Uses
Area of disk · Circumference Use in other formulae
Properties
Irrationality · Transcendence Less than 22/7
Value
Approximations · Memorization
People
Archimedes · Liu Hui · Zu Chongzhi Madhava of Sangamagrama William Jones · John Machin John Wrench · Ludolph van Ceulen
History
Chronology · Book
In culture
Legislation · Holiday
Related topics
Squaring the circle · Basel problem Tau (τ) · Other topics related to π
v · d · e

This page is about the history of approximations for the mathematical constant pi (π). There is a table summarizing the chronology of computation of π. See also the history of pi for other aspects of the evolution of our knowledge about mathematical properties of pi. Its first 50 decimal places are:

3.14159 26535 89793 23846 26433 83279 50288 41971 69399 37510.

Early history

Some Egyptologists^[1] have concluded that the ancient Egyptians used an approximation of pi in their monuments, as the Great Pyramid of Giza was built so that the circle whose radius is equal to the height of the pyramid has a circumference equal to the perimeter of the base (it is 1760 cubits around and 280 cubits in height)^[2] Others have argued that the ancient Egyptians had no concept of pi and would not have thought to encode it in their monuments. They argue, based on documents such as the Rhind papyrus, that the shapes of the pyramids are based on simple ratios of the sides of right angled triangles (the seked).,^[3] however, the Rhind Papyrus in fact shows that the Seked was derived from the base and height dimensions, and not the converse.^[4]

An Egyptian scribe named Ahmes wrote the oldest known text to imply an approximate value for pi. The Rhind Mathematical Papyrus dates from the Egyptian Second Intermediate Period — though Ahmes stated that he copied a Middle Kingdom papyrus (i.e. from before 1650 BCE). In problem 48 the area of a circle was computed by approximating the circle by an octagon. The value of pi is never mentioned or computed, however. If the Egyptians knew of pi, then the corresponding approximation was 256/81.^[3][5]

As early as the 19th century BCE, Babylonian mathematicians were using π ≈ 25/8, which is about 0.5 percent below the exact value.^{[citation needed]}

The Indian astronomer Yajnavalkya gave astronomical calculations in the Shatapatha Brahmana (c. 9th century BCE) that led to a fractional approximation of π ≈ 339/108 (which equals 3.13888..., which is correct to two decimal places when rounded, or 0.09 percent below the exact value).^{[citation needed]}

In the third century BCE, Archimedes proved the sharp inequalities ²²³⁄₇₁ < π < ²²⁄₇, by means of regular 96-gons; these values are 0.02 percent and 0.04 percent off, respectively. Later, in the second century CE, Ptolemy, using a regular 360-gon, obtained a value of 3.141666...., which is correct to three decimal places.^[6]

The Chinese mathematician Liu Hui in 263 CE computed pi to between 3.141024 and 3.142708 by inscribing an 96-gon and 192-gon; the average of these two values is 3.141864, an error of less than 0.01 percent. However, he suggested that 3.14 was a good enough approximation for practical purposes. Later he obtained a more accurate result π ≈ 3927/1250 = 3.1416.^{[citation needed]}

Middle ages

Until the year 1000 CE, pi was known to fewer than 10 decimal digits only.

In 499 CE India, mathematician Aryabhata calculated the value of pi to five significant figures (π ≈ 3.1416) in his astronomical treastise Āryabhaṭīya,^[7] and used the figures to work out a very close approximation of the earth's circumference.^[8] Contemporary mathematicians noted that Aryabhata might have even concluded that pi was an irrational number.^[9]

Aryabhata wrote in the second part of the Aryabhatiyam (gaṇitapāda 10):

chaturadhikam śatamaśṭaguṇam dvāśaśṭistathā sahasrāṇām
Ayutadvayaviśkambhasyāsanno vrîttapariṇahaḥ.

meaning:

Add four to one hundred, multiply by eight and then add sixty-two thousand. The result is approximately the circumference of a circle of diameter twenty thousand. By this rule the relation of the circumference to diameter is given.

In other words, (4 + 100) × 8 + 62000 is the circumference of a circle with diameter 20000. This provides a value of π ≈ 62832/20000 = 3.1416, correct to four decimal places. The commentator Nilakantha Somayaji (Kerala school of astronomy and mathematics, 15th century) has argued that the word āsanna (approaching), appearing just before the last word, here means not only that this is an approximation, but that the value is incommensurable (or irrational). However, the existence or usefulness of a rational approximation to a quantity does not mean the quantity is irrational. Also, the claim is only a conjecture, not a proof. The irrationality of pi was proved in Europe in 1761 by Lambert.

The 5th century Chinese mathematician and astronomer Zu Chongzhi computed pi between 3.1415926 and 3.1415927, which was correct to seven decimal places. He gave two other approximations of pi: π ≈ 22/7 and π ≈ 355/113.

In the 14th century, the Indian mathematician and astronomer Madhava of Sangamagrama, founder of the Kerala school of astronomy and mathematics, discovered the infinite series for pi, now known as the Madhava–Leibniz series,^[10][11] and gave two methods for computing the value of pi. One of these methods is to obtain a rapidly converging series by transforming the original infinite series of pi. By doing so, he obtained the infinite series

$\pi = \sqrt{12}\sum^\infty_{k=0} \frac{(-3)^{-k}}{2k+1} = \sqrt{12}\sum^\infty_{k=0} \frac{(-\frac{1}{3})^k}{2k+1} = \sqrt{12}\left(1-{1\over 3\cdot3}+{1\over5\cdot 3^2}-{1\over7\cdot 3^3}+\cdots\right)$

and used the first 21 terms to compute an approximation of pi correct to 11 decimal places as 3.14159265359.

The other method he used was to add a remainder term to the original series of pi. He used the remainder term

$\frac{n^2 + 1}{4n^3 + 5n}$

in the infinite series expansion of ^π⁄₄ to improve the approximation of pi to 13 decimal places of accuracy when n = 75.

The Persian mathematician and astronomer, Ghyath ad-din Jamshid Kashani (1380–1429), correctly computed 2π to 9 sexagesimal digits.^[12] This figure is equivalent to 16 decimal digits as

$2\pi = 6.2831853071795865 \,$

which equates to

$\pi = 3.14159265358979325. \,$

He achieved this level of accuracy by calculating the perimeter of a regular polygon with 3 × 2×10¹⁸ sides.^{[citation needed]}

16th to 19th centuries

The German mathematician Ludolph van Ceulen (circa 1600) computed the first 35 decimal places of pi. He was so proud of this accomplishment that he had them inscribed on his tombstone.

The Slovene mathematician Jurij Vega in 1789 calculated the first 140 decimal places for pi of which the first 126 were correct [2] and held the world record for 52 years until 1841, when William Rutherford calculated 208 decimal places of which the first 152 were correct. Vega improved John Machin's formula from 1706 and his method is still mentioned today.

The English amateur mathematician William Shanks, a man of independent means, spent over 20 years calculating pi to 707 decimal places. This was accomplished in 1873, although only the first 527 were correct. His routine was as follows: He would calculate new digits all morning; and then he would spend all afternoon checking his morning's work. This was the longest expansion of pi until the advent of the electronic digital computer three-quarters of a century later.

The Gauss–Legendre algorithm is used for calculating digits of pi.

20th century

In 1910, the Indian mathematician Srinivasa Ramanujan found several rapidly converging infinite series of pi, including

$\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum^\infty_{k=0} \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}$

which computes a further eight decimal places of pi with each term in the series. His series are now the basis for the fastest algorithms currently used to calculate pi.

From the mid-20th century onwards, all calculations of pi have been done with the help of calculators or computers.

In 1944, D. F. Ferguson, with the aid of a mechanical desk calculator, found that William Shanks had made a mistake in the 528th decimal place, and that all succeeding digits were incorrect.

In the early years of the computer, an expansion of pi to 100,265 decimal places^[13]:78 was computed by Maryland mathematician Dr. Daniel Shanks and his team at the United States Naval Research Laboratory (N.R.L.) in Washington, D.C. (Dr. Shanks's son Oliver Shanks, also a mathematician, states that there is no connection to William Shanks, and that his family's roots are in Central Europe.^{[citation needed]}

In 1961, Daniel Shanks and his team used two different power series for calculating the digits of pi. For one it was known that any error would produce a value slightly high, and for the other, it was known that any error would produce a value slightly low. And hence, as long as the two series produced the same digits, there was a very high confidence that they were correct. The first 100,000 digits of pi were published by the N.R.L.^{[13] :80–99} The authors outlined what would be needed to calculate pi to 1 million decimal places and concluded that the task was beyond that day's technology, but would be possible in five to seven years.^[13]:78

In 1989, the Chudnovsky brothers correctly computed pi to over a 1 billion decimal places on the supercomputer IBM 3090 using the following variation of Ramanujan's infinite series of pi:

$\frac{1}{\pi} = 12 \sum^\infty_{k=0} \frac{(-1)^k (6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 640320^{3k + 3/2}}.$

In 1999, Yasumasa Kanada and his team at the University of Tokyo correctly computed pi to over 200 billion decimal places on the supercomputer HITACHI SR8000/MPP (128 nodes) using another variation of Ramanujan's infinite series of pi. In October 2005 they claimed to have calculated it to 1.24 trillion places.^[14]

21st century – current claimed world record

In August 2009, a Japanese Supercomputer called the T2K Open Supercomputer was claimed to have more than doubled the previous record by calculating pi to 2.6 trillion digits in approximately 73 hours and 36 minutes.

In December 2009, Fabrice Bellard used a home computer to compute 2.7 trillion decimal digits of pi. Calculations were performed in base 2 (binary), then the result was converted to base 10 (decimal). The calculation, conversion, and verification steps took a total of 131 days.^[15]

In August 2010, Shigeru Kondo used Alexander Yee's y-cruncher to calculate 5 trillion digits of pi. This remains the world record for any type of calculation, but significantly it was performed on a home computer built by Kondo.^[16] The calculation was done between May 4 and August 3, with the primary and secondary verifications taking 64 and 66 hours respectively.^[17]In October 2011, they then broke their own record by correctly computing ten trillion digits using the same method but with better hardware.^[18]

Less accurate approximations

Some approximations which have been given for pi are notable in that they were less precise than previously known values.

Biblical value

It is sometimes claimed that the Bible implies that pi is about three, based on a passage in 1 Kings 7:23 and 2 Chronicles 4:2 giving measurements for the round basin located in front of the Temple in Jerusalem as having a diameter of 10 cubits and a circumference of 30 cubits. Rabbi Nehemiah explained this in his Mishnat ha-Middot (the earliest known Hebrew text on geometry, ca. 150 CE) by saying that the diameter was measured from the outside rim while the circumference was measured along the inner rim. This interpretation implies a brim 0.22535 cubit (or, assuming an 18-inch “cubit”, some 4 inches) thick, or roughly one “handbreadth” (cf. 1 Kings 7:24   and 2 Chronicles 4:3).

The interpretation of the biblical passage is still disputed,^[19][20] however, and other explanations have been offered, including that the measurements are given in round numbers (as the Hebrews tended to round off measurements to whole numbers^{[citation needed]}), or that cubits were not exact units, or that the basin may not have been exactly circular, or that the brim was wider than the bowl itself. Many reconstructions of the basin show a wider brim (or flared lip) extending outward from the bowl itself by several inches to match the description given in 1 Kings 7:26^[21] In the succeeding verses, the rim is described as "a handbreadth thick; and the brim thereof was wrought like the brim of a cup, like the flower of a lily: it received and held three thousand baths" 2 Chronicles 4:5, which suggests a shape that can be encompassed with a string shorter than the total length length of the brim, e.g., a Lilium flower or a Teacup.

The issue is discussed in the Talmud and in Rabbinic literature.^[22] Among the many explanations and comments are these:

• In 1 Kings 7:23 the word translated 'measuring line' appears in the Hebrew text spelled QWH קַוה, but elsewhere the word is most usually spelled QW קַו. The ratio of the numerical values of these Hebrew spellings is ¹¹¹⁄₁₀₆. If the putative value of 3 is multiplied by this ratio, one obtains ³³³⁄₁₀₆ = 3.141509433... – within 1/10,000th of the true value of pi, a convergent for pi which is more accurate than ²²⁄₇, although not as good as the next one ³⁵⁵⁄₁₁₃.
• Maimonides states (ca. 1168 CE) that pi can only be known approximately, so the value 3 was given as accurate enough for religious purposes. This is taken by some^[23] as the earliest assertion that pi is irrational.

Another explanation is that the 10-cubit measurement was from "brim to brim" or "lip to lip." That is, the ritual bath had a brim or lip which protruded beyond the main body of the vessel. The 10 cubits is described as the measurement from brim to brim, and a 30 cubit cord could completely encircle the main body of the vessel below the lip.

The Indiana bill

The "Indiana Pi Bill" of 1897, which never passed out of the committee of the Indiana General Assembly in the U.S., has been claimed to imply a number of different values for pi, although the closest it comes to explicitly asserting one is the wording "the ratio of the diameter and circumference is as five-fourths to four", which would make π = 16/5 = 3.2, a discrepancy of nearly 2 percent.

Development of efficient formulae

Main article: List of formulae involving π

Machin-like formulae

For fast calculations, one may use formulae such as Machin's:

$\frac{\pi}{4} = 4 \arctan\frac{1}{5} - \arctan\frac{1}{239}$

together with the Taylor series expansion of the function arctan(x). This formula is most easily verified using polar coordinates of complex numbers, producing:

$(5+i)^4\cdot(-239+i)=-114244-114244i.$

Another example is:

$\frac{\pi}{4} = \arctan\frac{1}{2} + \arctan\frac{1}{3}$

which is verified as above as producing a 45° vector:

$(2+i)\cdot(3+i) = 5+5i.$

Formulae of this kind are known as Machin-like formulae.

Other classical formulae

Other formulae that have been used to compute estimates of pi include:

Liu Hui:

$\begin{align} \pi \approxeq 768 \sqrt{2 - \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2+1}}}}}}}}} \approxeq 3.141590463236763. \end{align}$

Madhava:

$\pi = \sqrt{12}\sum^\infty_{k=0} \frac{(-3)^{-k}}{2k+1} = \sqrt{12}\sum^\infty_{k=0} \frac{(-\frac{1}{3})^k}{2k+1} = \sqrt{12}\left({1\over 1\cdot3^0}-{1\over 3\cdot3^1}+{1\over5\cdot 3^2}-{1\over7\cdot 3^3}+\cdots\right)$

Euler:

${\pi} = 20 \arctan\frac{1}{7} + 8 \arctan\frac{3}{79}$

Newton:

$\frac{\pi}{2}= \sum_{k=0}^\infty\frac{k!}{(2k+1)!!}= \sum_{k=0}^{\infty} \cfrac {2^k k!^2}{(2k + 1)!} = 1+\frac{1}{3}\left(1+\frac{2}{5}\left(1+\frac{3}{7}\left(1+\cdots\right)\right)\right)$

Ramanujan:

$\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum^\infty_{k=0} \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}$

David Chudnovsky and Gregory Chudnovsky:

$\frac{1}{\pi} = 12 \sum^\infty_{k=0} \frac{(-1)^k (6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 640320^{3k + 3/2}}$

Ramanujan's work is the basis for the Chudnovsky algorithm, the fastest algorithms used, as of the turn of the millennium, to calculate pi.

Modern algorithms

Extremely long decimal expansions of pi are typically computed with iterative formulae like the Gauss–Legendre algorithm and Borwein's algorithm. The latter, found in 1985 by Jonathan and Peter Borwein, converges extremely fast:

For $y_0=\sqrt2-1,\ a_0=6-4\sqrt2$ and

$y_{k+1}=(1-f(y_k))/(1+f(y_k)) ~,~ a_{k+1} = a_k(1+y_{k+1})^4 - 2^{2k+3} y_{k+1}(1+y_{k+1}+y_{k+1}^2)$

where f(y) = (1 − y⁴)^{1 / 4}, the sequence 1 / a_k converges quartically to pi, giving about 100 digits in three steps and over a trillion digits after 20 steps.

The first one million digits of pi and ¹⁄_π are available from Project Gutenberg (see external links below). A former calculation record (December 2002) by Yasumasa Kanada of Tokyo University stood at 1.2 billion digits, which were computed in September 2002 on a 64-node Hitachi supercomputer with 1 terabyte of main memory, which carries out 2 trillion operations per second, nearly twice as many as the computer used for the previous record (206 billion digits). The following Machin-like formulæ were used for this:

$\frac{\pi}{4} = 12 \arctan\frac{1}{49} + 32 \arctan\frac{1}{57} - 5 \arctan\frac{1}{239} + 12 \arctan\frac{1}{110443}$

K. Takano (1982).

$\frac{\pi}{4} = 44 \arctan\frac{1}{57} + 7 \arctan\frac{1}{239} - 12 \arctan\frac{1}{682} + 24 \arctan\frac{1}{12943}$ (F. C. W. Störmer (1896)).

These approximations have so many digits that they are no longer of any practical use, except for testing new supercomputers. (Normality of pi will always depend on the infinite string of digits on the end, not on any finite computation.)

Formulae for binary digits

Main article: Bailey–Borwein–Plouffe formula

In 1997, David H. Bailey, Peter Borwein and Simon Plouffe published a paper (Bailey, 1997) on a new formula for pi as an infinite series:

$\pi = \sum_{k = 0}^{\infty} \frac{1}{16^k} \left( \frac{4}{8k + 1} - \frac{2}{8k + 4} - \frac{1}{8k + 5} - \frac{1}{8k + 6}\right).$

This formula permits one to easily compute the k^th binary or hexadecimal digit of pi, without having to compute the preceding k − 1 digits. Bailey's website contains the derivation as well as implementations in various programming languages. The PiHex project computed 64-bits around the quadrillionth bit of pi (which turns out to be 0).

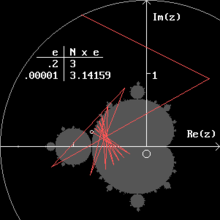Obtaining an approximate value of pi by counting iterations of a complex number. The example red trajectory of N = 15 iterations starts from the value (−0.75, e) shown as a white spot, where the desired precision is e = 0.2, and gives the result π = 3 ± 0.2. Any greater precision is obtainable by reducing e which will yield more iterations. The Mandelbrot set is shown in grey and the starting point lies slightly above the bottom of the "seahorse valley" at (−0.75, 0).

Pi and a fractal

A feature of the Mandelbrot set recently reported^[24] gives a means to calculate an approximate value of pi to any chosen accuracy, without seeking the limit of an infinite series. One assigns

$n = 0, \quad z = c = -\frac{3}{4} + ei \quad (e>0)$

where e is the precision required (e.g. $e=10^{-k},\;k\in\mathbb{N}_+$ gives pi to k decimal places), and applies the iteration (note that n is just the number of iterations):

$n \mapsto n + 1, \quad z \mapsto z^2 + c \quad \hbox{ while } \quad |z|<2$

The result is simply the approximation

$\pi = ne \pm e \,$

In the graphical view one starts iterating from a point just above the bottom of the "seahorse valley" of the Mandelbrot set at (−0.75, 0).

Miscellaneous approximations

Historically, for a long time the base 60 was used for calculations. In this base, pi can be approximated to eight (decimal) significant figures as

$3 + \frac{8}{60} + \frac{29}{60^2} + \frac{44}{60^3} = 3.14159\ 259^+$

(The next sexagesimal digit is 0, causing truncation here to yield a relatively good approximation.)

In addition, the following expressions can be used to estimate pi:

• accurate to three digits:

$\sqrt{2} + \sqrt{3} = 3.146^+$

Karl Popper conjectured that Plato knew this expression, that he believed it to be exactly pi, and that this is responsible for some of Plato's confidence in the omnicompetence of mathematical geometry—and Plato's repeated discussion of special right triangles that are either isosceles or halves of equilateral triangles.

• accurate to four digits:

$\sqrt{7+\sqrt{6+\sqrt{5}}} = 3.14163^+$^[25]

• accurate to four digits:

$\sqrt[3]{31} = 3.1413^+$^[26]

• an approximation by Ramanujan, accurate to 4 digits:

$\frac{9}{5}+\sqrt{\frac{9}{5}} = 3.14164^+$

• accurate to five digits:

$\frac{7^7}{4^9} = 3.14156\ 7230^+$

• accurate to seven digits:

$\frac{355}{113} = 3.14159\ 29^+$

• accurate to nine digits:

$\sqrt[4]{\frac{2143}{22}} = 3.14159\ 26525^+$

This is from Ramanujan, who claimed the goddess Namagiri appeared to him in a dream and told him the true value of pi.^{[citation needed]}

• accurate to ten digits:

$\frac{63}{25} \times \frac{17 + 15\sqrt{5}}{7 + 15\sqrt{5}} = 3.14159\ 26538^+$

• accurate to ten digits:

$\sqrt[193]{\frac{10^{100}}{11222.11122}} = 3.14159\ 26536^+$

This curious approximation follows the observation that the -193rd power of pi yields the sequence 1122211125... Replacing 5 by 2 completes the symmetry without reducing the correct digits of pi, while inserting a central decimal point remarkably fixes the accompanying magnitude at 10¹⁰⁰.^[27]

• accurate to 18 digits:

$\frac{80\sqrt{15}(5^4+53\sqrt{89})^\frac{3}{2}}{3308(5^4+53\sqrt{89})-3\sqrt{89}}$^[28]

This is based on the fundamental discriminant d = 3(89) = 267 which has class number h(-d) = 2 explaining the algebraic numbers of degree 2. Note that the core radical is 5³ more than the fundamental unit $\scriptstyle U_{89} = 500+53\sqrt{89}$ which gives the smallest solution {x, y} = {500, 53} to the Pell equation x²-89y² = -1.

• accurate to 30 decimal places:

$\frac{\ln(640320^3+744)}{\sqrt{163}} = 3.14159\ 26535\ 89793\ 23846\ 26433\ 83279^+$

This is a consequence of the closeness of the Ramanujan constant to the integer 640320³+744. This does not admit obvious generalizations, because there are only finitely many Heegner numbers and 163 is the largest one. One possible generalization, though (also a consequence of value of the j-invariant on a lattice with complex multiplication), is the following, perhaps not as impressive, but accurate to 52 decimal places:

$\frac{\ln(5280^3(236674+30303\sqrt{61})^3+744)}{\sqrt{427}}$

• The continued fraction representation of pi can be used to generate successive best rational approximations. These approximations are the best possible rational approximations of pi relative to the size of their denominators. Here is a list of the first of these, punctuated at significant steps:

  $\frac{3}{1},\quad \frac{13}{4},\frac{16}{5},\frac{19}{6},\frac{22}{7},\quad \frac{179}{57},\frac{201}{64}, \frac{223}{71},\frac{245}{78},\frac{267}{85},\frac{289}{92},\frac{311}{99},\frac{333}{106},\quad \frac{355}{113},\quad \frac{52163}{16604}$

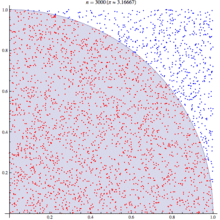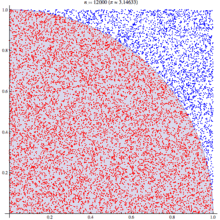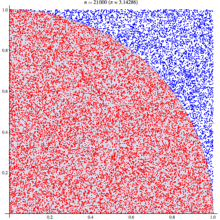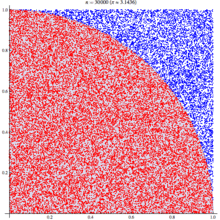
Summing a circle's area

Numerical approximation of pi: as points are randomly scattered inside the unit square, some fall within the unit circle. The fraction of points inside the circle approaches π/4 as points are added. Note: Press ESC to pause this animation.

Pi can be obtained from a circle if its radius and area are known. Since the area of a circle is given by this formula:

$A = \pi r^2.\$

If a circle with radius r is drawn with its center at the point (0, 0), any point whose distance from the origin is less than r will fall inside the circle. The Pythagorean theorem gives the distance from any point (x, y) to the center:

$d=\sqrt{x^2+y^2}.\!$

Mathematical "graph paper" is formed by imagining a 1×1 square centered around each cell (x, y), wherex and y are integers between −r and r. Squares whose center resides inside or exactly on the border of the circle can then be counted by testing whether, for each cell (x, y),

$\sqrt{x^2+y^2} \le r.\!$

The total number of cells satisfying that condition thus approximates the area of the circle, which then can be used to calculate an approximation of pi. Closer approximations can be produced by using larger values of r.

Mathematically, this formula can be written:

$\pi = \lim_{r \to \infty} \frac{1}{r^2} \sum_{x=-r}^{r} \; \sum_{y=-r}^{r} \begin{cases} 1 & \text{if } \sqrt{x^2+y^2} \le r \\ 0 & \text{if } \sqrt{x^2+y^2} > r. \end{cases}$

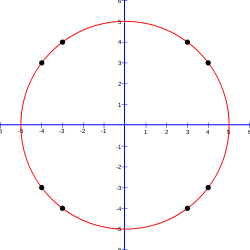
In other words, begin by choosing a value for r. Consider all cells (x, y) in which bothx and y are integers between −r and r. Starting at 0, add 1 for each cell whose distance to the origin (0,0) is less than or equal to r. When finished, divide the sum, representing the area of a circle of radius r, by r² to find the approximation of pi. For example, if r is 5, then the cells considered are:

(−5,5)	(−4,5)	(−3,5)	(−2,5)	(−1,5)	(0,5)	(1,5)	(2,5)	(3,5)	(4,5)	(5,5)
(−5,4)	(−4,4)	(−3,4)	(−2,4)	(−1,4)	(0,4)	(1,4)	(2,4)	(3,4)	(4,4)	(5,4)
(−5,3)	(−4,3)	(−3,3)	(−2,3)	(−1,3)	(0,3)	(1,3)	(2,3)	(3,3)	(4,3)	(5,3)
(−5,2)	(−4,2)	(−3,2)	(−2,2)	(−1,2)	(0,2)	(1,2)	(2,2)	(3,2)	(4,2)	(5,2)
(−5,1)	(−4,1)	(−3,1)	(−2,1)	(−1,1)	(0,1)	(1,1)	(2,1)	(3,1)	(4,1)	(5,1)
(−5,0)	(−4,0)	(−3,0)	(−2,0)	(−1,0)	(0,0)	(1,0)	(2,0)	(3,0)	(4,0)	(5,0)
(−5,−1)	(−4,−1)	(−3,−1)	(−2,−1)	(−1,−1)	(0,−1)	(1,−1)	(2,−1)	(3,−1)	(4,−1)	(5,−1)
(−5,−2)	(−4,−2)	(−3,−2)	(−2,−2)	(−1,−2)	(0,−2)	(1,−2)	(2,−2)	(3,−2)	(4,−2)	(5,−2)
(−5,−3)	(−4,−3)	(−3,−3)	(−2,−3)	(−1,−3)	(0,−3)	(1,−3)	(2,−3)	(3,−3)	(4,−3)	(5,−3)
(−5,−4)	(−4,−4)	(−3,−4)	(−2,−4)	(−1,−4)	(0,−4)	(1,−4)	(2,−4)	(3,−4)	(4,−4)	(5,−4)
(−5,−5)	(−4,−5)	(−3,−5)	(−2,−5)	(−1,−5)	(0,−5)	(1,−5)	(2,−5)	(3,−5)	(4,−5)	(5,−5)

This circle as it would be drawn on a Cartesian coordinate graph. The cells (±3, ±4) and (±4, ±3) are labeled.

The 12 cells (0, ±5), (±5, 0), (±3, ±4), (±4, ±3) are exactly on the circle, and 69 cells are completely inside, so the approximate area is 81, and pi is calculated to be approximately 3.24 because 81 / 5² = 3.24. Results for some values of r are shown in the table below:

r	area	approximation of pi
2	13	3.25
3	29	3.22222
4	49	3.0625
5	81	3.24
10	317	3.17
20	1257	3.1425
100	31417	3.1417
1000	3141549	3.141549

Similarly, the more complex approximations of pi given below involve repeated calculations of some sort, yielding closer and closer approximations with increasing numbers of calculations.

Approximation with a regular polygon

Pi is defined as the ratio of the circumference of a circle to its diameter. Circles can be approximated as regular polygons with an increasing number of sides, approaching infinity. Archimedes used this method with a 96-sided polygon to show that pi is between 223/71 and 22/7.

Continued fractions

Besides its simple continued fraction representation [3; 7, 15, 1, 292, 1, 1, …], which displays no discernible pattern, pi has many generalized continued fraction representations generated by a simple rule, including these two.

$\pi= {3 + \cfrac{1^2}{6 + \cfrac{3^2}{6 + \cfrac{5^2}{6 + \ddots\,}}}}\!$

$\pi = \cfrac{4}{1 + \cfrac{1^2}{3 + \cfrac{2^2}{5 + \cfrac{3^2}{7 + \ddots}}}}\!$

(Other representations are available at The Wolfram Functions Site.)

Trigonometry

Gregory–Leibniz series

The Gregory–Leibniz series

$\pi = 4\sum_{n=0}^{\infty} \cfrac {(-1)^n}{2n+1} = 4\left( \frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} +- \cdots\right) \! = \cfrac{4}{1 + \cfrac{1^2}{2 + \cfrac{3^2}{2 + \cfrac{5^2}{2 + \ddots}}}}\!$

is the power series for arctan(x) specialized to x = 1. It converges too slowly to be of practical interest. However, the power series converges much faster for smaller values of x, which leads to formulas where π arises as the sum of small angles with rational tangents, such as these two by John Machin:

$\pi = 4\arctan\frac{1}{2} + 4\arctan\frac{1}{3}\!$

$\pi = 16\arctan\frac{1}{5} - 4\arctan\frac{1}{239}.\!$

Formulas for pi of this type are known as Machin-like formulae.

Arctangent

Further information: Factorial#Double factorial

Knowing that $4\arctan(1) = \pi\!$ the formula can be simplified to get:

$\pi = 2\sum_{n=0}^{\infty} \cfrac {n!}{(2n + 1)!!} = \sum_{n=0}^{\infty} \cfrac {2^{n+1} n!^2} {(2n + 1)!} = \sum_{n=0}^{\infty} \cfrac {2^{n+1}} {\binom {2n} n (2n + 1)} \!$

$= 2\left( 1 + \cfrac{1}{3} + \cfrac{1\cdot2}{3\cdot5} + \cfrac{1\cdot2\cdot3}{3\cdot5\cdot7} + \cfrac{1\cdot2\cdot3\cdot4}{3\cdot5\cdot7\cdot9} + \cfrac{1\cdot2\cdot3\cdot4\cdot5}{3\cdot5\cdot7\cdot9\cdot11} + \cdots\right) \!$

$= 2 + \frac{2}{3} + \frac{4}{15} + \frac{4}{35} + \frac{16}{315} + \frac{16}{693} + \frac{32}{3003} + \frac{32}{6435} + \frac{256}{109395} + \frac{256}{230945} + \cdots\!$

with a convergence such that each additional 10 terms yields at least three more digits.

Arcsine

Observing an equilateral triangle and noting that

$\sin\left (\frac{\pi}{6}\right )=\frac{1}{2}\!$

yields

$\pi = 3 \sum_{n=0}^\infty \frac {\binom {2n} n} {16^n (2n+1)} = \sum_{n=0}^\infty \frac {3\cdot \frac{2}{1} \frac{6}{2} \frac{10}{3} \cdots \frac{4n-2}{n}} {16^n(2n+1)} = \frac {3} {16^0 \cdot 1} + \frac {6} {16^1 \cdot 3} + \frac {18} {16^2 \cdot 5} + \frac {60} {16^3 \cdot 7} + \cdots\!$

$= 3 + \frac{1}{8} + \frac{9}{640} + \frac{15}{7168} + \frac{35}{98304} + \frac{189}{2883584} + \cfrac{693}{54525952} + \frac{429}{167772160} + \cdots\!$

with a convergence such that each additional five terms yields at least three more digits.

The Salamin–Brent algorithm

The Gauss–Legendre algorithm or Salamin–Brent algorithm was discovered independently by Richard Brent and Eugene Salamin in 1975. This can compute π to N digits in time proportional to $N\,\log(N)\,\log(\log(N))$, much faster than the trigonometric formulae.

Digit extraction methods

The Bailey–Borwein–Plouffe formula (BBP) for calculating pi was discovered in 1995 by Simon Plouffe. The formula computes pi in base 16 without needing to compute the previous digits (digit extraction). ^[29]

$\pi=\sum_{n=0}^\infty \left(\frac{4}{8n+1}-\frac{2}{8n+4}-\frac{1}{8n+5}-\frac{1}{8n+6}\right)\left(\frac{1}{16}\right)^n\!$

In 1996, Simon Plouffe derived an algorithm to extract the nth digit of pi in an arbitrary base in O(n³log(n)³) time.^[30] In 1997, this was improved to O(n²) by Fabrice Bellard, who derived an alternative formula for computing pi in base 2.^[31]

$\pi=\frac{1}{2^6}\sum_{n=0}^\infty \frac{(-1)^n}{2^{10n}} \left (-\frac{2^5}{4n+1}-\frac{1}{4n+3}+\frac{2^8}{10n+1}-\frac{2^6}{10n+3}-\frac{2^2}{10n+5}-\frac{2^2}{10n+7}+\frac{1}{10n+9}\right )\!$

Efficient methods

In 1961 the first expansion of pi to 100,000 decimal places was computed by Maryland mathematician Dr. Daniel Shanks and his team at the United States Naval Research Laboratory (N.R.L.).

Daniel Shanks and his team used two different power series for calculating the digits of pi. For one it was known that any error would produce a value slightly high, and for the other, it was known that any error would produce a value slightly low. And hence, as long as the two series produced the same digits, there was a very high confidence that they were correct. The first 100,000 digits of pi were published by the Naval Research Laboratory.

None of the formulæ given above can serve as an efficient way of approximating pi. For fast calculations, one may use a formula such as Machin's:

$\frac{\pi}{4} = 4 \arctan\frac{1}{5} - \arctan\frac{1}{239}\!$

together with the Taylor series expansion of the function arctan(x). This formula is most easily verified using polar coordinates of complex numbers, starting with,

$(5+i)^4\cdot(239-i)=2^2 \cdot 13^4(1+i).\!$

Formulae of this kind are known as Machin-like formulae. (Note also that {x,y} = {239, 13²} is a solution to the Pell equation x²-2y² = -1.)

Many other expressions for pi were developed and published by Indian mathematician Srinivasa Ramanujan. He worked with mathematician Godfrey Harold Hardy in England for a number of years.

Extremely long decimal expansions of pi are typically computed with the Gauss–Legendre algorithm and Borwein's algorithm; the Salamin–Brent algorithm which was invented in 1976 has also been used.

The first one million digits of pi and ¹/_π are available from Project Gutenberg (see external links below). The record as of December 2002 by Yasumasa Kanada of Tokyo University stands at 1,241,100,000,000 digits, which were computed in September 2002 on a 64-node Hitachi supercomputer with 1 terabyte of main memory, which carries out 2 trillion operations per second, nearly twice as many as the computer used for the previous record (206 billion digits). The following Machin-like formulæ were used for this:

$\frac{\pi}{4} = 12 \arctan\frac{1}{49} + 32 \arctan\frac{1}{57} - 5 \arctan\frac{1}{239} + 12 \arctan\frac{1}{110443}\!$

K. Takano (1982).

$\frac{\pi}{4} = 44 \arctan\frac{1}{57} + 7 \arctan\frac{1}{239} - 12 \arctan\frac{1}{682} + 24 \arctan\frac{1}{12943}\!$

F. C. W. Störmer (1896).

These approximations have so many digits that they are no longer of any practical use, except for testing new supercomputers. (Normality of pi will always depend on the infinite string of digits on the end, not on any finite computation.)

In 1997, David H. Bailey, Peter Borwein and Simon Plouffe published a paper (Bailey, 1997) on a new formula for pi as an infinite series:

$\pi = \sum_{k = 0}^{\infty} \frac{1}{16^k} \left( \frac{4}{8k + 1} - \frac{2}{8k + 4} - \frac{1}{8k + 5} - \frac{1}{8k + 6}\right).\!$

This formula permits one to fairly readily compute the k^th binary or hexadecimal digit of pi, without having to compute the preceding k − 1 digits. Bailey's website contains the derivation as well as implementations in various programming languages. The PiHex project computed 64-bits around the quadrillionth bit of pi (which turns out to be 0).

Fabrice Bellard claims to have beaten the efficiency record set by Bailey, Borwein, and Plouffe with his formula to calculate binary digits of pi [3]:

$\pi = \frac{1}{2^6} \sum_{n=0}^{\infty} \frac{{(-1)}^n}{2^{10n}} \left( - \frac{2^5}{4n+1} - \frac{1}{4n+3} + \frac{2^8}{10n+1} - \frac{2^6}{10n+3} - \frac{2^2}{10n+5} - \frac{2^2}{10n+7} + \frac{1}{10n+9} \right)\!$

Other formulae that have been used to compute estimates of pi include:

$\frac{\pi}{2}=\sum_{k=0}^\infty\frac{k!}{(2k+1)!!}=\sum_{k=0}^{\infty}\frac{2^k k!^2}{(2k+1)!} =1+\frac{1}{3}\left(1+\frac{2}{5}\left(1+\frac{3}{7}\left(1+\cdots\right)\right)\right)\!$

Newton.

$\frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum^\infty_{k=0} \frac{(4k)!(1103+26390k)}{(k!)^4 396^{4k}}\!$

Srinivasa Ramanujan.

This converges extraordinarily rapidly. Ramanujan's work is the basis for the fastest algorithms used, as of the turn of the millennium, to calculate pi.

$\frac{1}{\pi} = 12 \sum^\infty_{k=0} \frac{(-1)^k (6k)! (13591409 + 545140134k)}{(3k)!(k!)^3 640320^{3k + 3/2}}\!$

David Chudnovsky and Gregory Chudnovsky.

Projects

Pi Hex

Pi Hex was a project to compute three specific binary digits of pi using a distributed network of several hundred computers. In 2000, after two years, the project finished computing the five trillionth (10¹²), the forty trillionth, and the quadrillionth (10¹⁵) bits. All three of them turned out to be 0.

Software for calculating pi

Over the years, several programs have been written for calculating pi to many digits on personal computers.

General purpose

Most computer algebra systems can calculate pi and other common mathematical constants to any desired precision.

Functions for calculating pi are also included in many general libraries for arbitrary-precision arithmetic, for instance CLN and MPFR.

An example of a web-based computer script (written in PHP) has been made to calculate pi and is below. It is designed to be able to follow Viète's formula for calculating pi and if this script is given enough time to run, it can display 1000 digits of pi.

<?php
set_time_limit(0);
echo '<br />';
 
$digits=1000;
$pival='1';
$str1='';
while ($pirow<2000)
    {
    $pirow+=1;
    $pisubrow=0;
    $tempval='0';
    while ($pisubrow<$pirow)
        {
        $tempval=bcsqrt(bcadd('2',$tempval,$digits),$digits);
        $pisubrow+=1;
        sleep(1);
        }
    $tempval=bcdiv('2',$tempval,$digits);
    $pival=bcmul($tempval,$pival,$digits);
    unset($tempval);      
    $tempval=bcmul('2',$pival,$digits);
    $common = array();
    $length = (strlen($str1) >= strlen($tempval)) ? strlen($str1) : strlen($tempval);
    for($x=0;$x<$length;$x++){
        if($str1[$x] == $tempval[$x]){
            $common[] = $str1[$x]; 
        }else{
            break;
        }
    }
    if ($pirow>5)
        {
        echo 'pi='.substr(join('',$common),0,-2);
        }
    unset($str1);
    $str1=$tempval;    
    unset($tempval);
    echo '<p>';
    flush();
    sleep(1);
    }
$pival=bcmul($pival,'2',$digits);
unset($pirow);
?>

The above PHP script will need to be given at least two minutes for a useful result to be displayed. The script can continue to run for days with no errors. If there is no worry about CPU usage in this script then the lines with the sleep() function can be removed for a faster result.

Special purpose

Programs designed for calculating pi may have better performance than general-purpose mathematical software. They typically implement checkpointing and efficient disk swapping to facilitate extremely long-running and memory-expensive computations.

• y-cruncher by Alexander Yee^[32] is the program for which the current world record number of digits was calculated by Shigeru Kondo, of 10 trillion digits on 19 October 2011. This a record for both super computers as well as home-built computers. y-cruncher calculates other constants as well and holds world records for large runs of most of them.

• PiFast by Xavier Gourdon was the fastest program for Microsoft Windows in 2003. According to its author, it can compute one million digits in 3.5 seconds on a 2.4 GHz Pentium 4.^[33] PiFast can also compute other irrational numbers like e and √2. It can also work at lesser efficiency with very little memory (down to a few tens of megabytes to compute well over a billion (10⁹) digits). This tool is a popular benchmark in the overclocking community. PiFast 4.4 is available from Stu's Pi page. PiFast 4.3 is available from Gourdon's page.

• QuickPi by Steve Pagliarulo for Windows is faster than PiFast for runs of under 400 million digits. Version 4.5 is available on Stu's Pi Page below. Like PiFast, QuickPi can also compute other irrational numbers like e, √2, and √3. The software may be obtained from the Pi-Hacks Yahoo! forum, or from Stu's Pi page.

• Super PI by Kanada Laboratory^[34] in the University of Tokyo is the program for Microsoft Windows for runs from 16,000 to 33,550,000 digits. It can compute one million digits in 40 minutes and two million digits in 90 minutes and four million digits in 220 minutes on a Pentium 90 MHz. Super PI version 1.1 is available from Super PI 1.1 page.

References

1. ^ Petrie, W.M.F. Wisdom of the Egyptians (1940)
2. ^ Verner, Miroslav. The Pyramids: The Mystery, Culture, and Science of Egypt's Great Monuments. Grove Press. 2001 (1997). ISBN 0-8021-3935-3
3. ^ ^{a b} Rossi, Corinna Architecture and Mathematics in Ancient Egypt, Cambridge University Press. 2007 ISBN 978-0521690539
4. ^ Legon, J.A.R. On Pyramid Dimensions and Proportions (1991) Discussions in Egyptology (20) 25-34 [1]
5. ^ Katz, Victor J. (editor),Imhausen, Annette et.al. The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook, Princeton University Press. 2007ISBN 978-0691114859
6. ^ Smith DE (1911). The Teaching of Geometry. Ginn and Company: Boston. p. 279. ISBN 0807745316. 
7. ^ Jacobs, Harold R. (2003). Geometry: Seeing, Doing, Understanding (Third Edition). New York: W.H. Freeman and Company. p. 70. 
8. ^ "Aryabhata the Elder". University of St Andrews, School of Mathematics and Statistics. http://www-history.mcs.st-and.ac.uk/Biographies/Aryabhata_I.html. Retrieved 20 July 2011. 
9. ^ S. Balachandra Rao (1994/1998). Indian Mathematics and Astronomy: Some Landmarks. Jnana Deep Publications. ISBN 81-7371-205-0. 
10. ^ George E. Andrews, Richard Askey, Ranjan Roy (1999). Special Functions. Cambridge University Press. p. 58. ISBN 0521789885 
11. ^ Gupta, R. C. (1992). "On the remainder term in the Madhava–Leibniz's series". Ganita Bharati 14 (1-4): 68–71 
12. ^ Al-Kashi, author: Adolf P. Youschkevitch, chief editor: Boris A. Rosenfeld, p. 256
13. ^ ^{a b c} Shanks, D.; Wrench, Jr., J. W. (1962). "Calculation of π to 100,000 decimals". Mathematics of Computation (American Mathematical Society) 16 (77): 76–99. doi:10.2307/2003813. JSTOR 2003813 .
14. ^ Announcement at the Kanada lab web site.
15. ^ Bellard.org
16. ^ McCormick Grad Sets New Pi Record
17. ^ 5 Trillion Digits of Pi - New World Record
18. ^ http://www.newscientist.com/blogs/shortsharpscience/2011/10/pi-10-trillion.html
19. ^ Aleff, H. Peter. "Ancient Creation Stories told by the Numbers: Solomon's Pi". recoveredscience.com. http://www.recoveredscience.com/const303solomonpi.htm. Retrieved 2007-10-30. 
20. ^ O'Connor, J J; E F Robertson (2001-08). "A history of Pi". http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Pi_through_the_ages.html. Retrieved 2007-10-30. 
21. ^ Math Forum – Ask Dr. Math
22. ^ Tsaban, B; Boaz Tsaban, David Garber (February 1998). "On the rabbinical approximation of π". Historia Mathematica 25 (1): 75–84. doi:10.1006/hmat.1997.2185. ISSN 0315-0860. http://u.cs.biu.ac.il/~tsaban/Pdf/latexpi.pdf. Retrieved 2009-07-14. 
23. ^ Wilbur Richard Knorr, The Ancient Tradition of Geometric Problems, New York: Dover Publications, 1993.
24. ^ "π in the Mandelbrot set". https://home.comcast.net/~davejanelle/mandel.pdf. 
25. ^ A nested radical approximation for pi
26. ^ Gardner, Martin (1995). New Mathematical Diversions. Mathematical Association of America. p. 92 .
27. ^ Hoffman, D.W. College Mathematics Journal, 40 (2009) 399
28. ^ CetinHakimoglu–Brown
29. ^ MathWorld: BBP Formula Wolfram.com
30. ^ Simon Plouffe, On the computation of the n'th decimal digit of various transcendental numbers, November 1996
31. ^ Bellard's Website: Bellard.org
32. ^ y-cruncher
33. ^ "PiFast timings"
34. ^ Takahashi, Daisuke & Kanada, Yasumasa (10 August 2010). "Kanada Laboratory home page". University of Tokyo. http://pi2.cc.u-tokyo.ac.jp/index.html. Retrieved 1 May 2011. 

Notes

• Bailey, David H., Borwein, Peter B., and Plouffe, Simon (April 1997). "On the Rapid Computation of Various Polylogarithmic Constants". Mathematics of Computation 66 (218): 903–913. doi:10.1090/S0025-5718-97-00856-9. http://crd.lbl.gov/~dhbailey/dhbpapers/digits.pdf. 
• Joseph, George G. (2000). The Crest of the Peacock: Non-European Roots of Mathematics (New ed., London : Penguin ed.). London: Penguin. ISBN 0-14-027778-1. 
• Jackson, K and Stamp, J. (2002). Pyramid: Beyond Imagination. Inside the Great Pyramid of Giza. London: BBC.