Rate of convergence

In numerical analysis, the speed at which a convergent sequence approaches its limit is called the rate of convergence. Although strictly speaking, a limit does not give information about any finite first part of the sequence, this concept is of practical importance if we deal with a sequence of successive approximations for an iterative method, as then typically fewer iterations are needed to yield a useful approximation if the rate of convergence is higher. This may even make the difference between needing ten or a million iterations.

Similar concepts are used for discretization methods. The solution of the discretized problem converges to the solution of the continuous problem as the grid size goes to zero, and the speed of convergence is one of the factors of the efficiency of the method. However, the terminology in this case is different from the terminology for iterative methods.

Series acceleration is a collection of techniques for improving the rate of convergence of a series. Such acceleration is commonly accomplished with sequence transformations.

Convergence speed for iterative methods

Basic definition

Suppose that the sequence {x_k} converges to the number L.

We say that this sequence converges linearly to L, if there exists a number μ ∈ (0, 1) such that

$\lim_{k\to \infty} \frac{|x_{k+1}-L|}{|x_k-L|} = \mu.$

The number μ is called the rate of convergence.

If the sequences converges, and

• μ = 0, then the sequence is said to converge superlinearly.
• μ = 1, then the sequence is said to converges sublinearly.

If the sequences converges sublinearly and additionally

$\lim_{k\to \infty} \frac{|x_{k+2} - x_{k+1}|}{|x_{k+1} - x_k|} = 1,$

then it is said the sequence {x_k} converges logarithmically to L.

The next definition is used to distinguish superlinear rates of convergence. We say that the sequence converges with order q for q > 1 to L if

$\lim_{k\to \infty} \frac{|x_{k+1}-L|}{|x_k-L|^q} = \mu \,\big|\; \mu > 0.$

In particular, convergence with order

• 2 is called quadratic convergence,
• 3 is called cubic convergence,
• etc.

This is sometimes called Q-linear convergence, Q-quadratic convergence, etc., to distinguish it from the definition below. The Q stands for "quotient," because the definition uses the quotient between two successive terms.

Extended definition

The drawback of the above definitions is that these do not catch some sequences which still converge reasonably fast, but whose "speed" is variable, such as the sequence {b_k} below. Therefore, the definition of rate of convergence is sometimes extended as follows.

Under the new definition, the sequence {x_k} converges with at least order q if there exists a sequence {ε_k} such that

$|x_k - L|\le\varepsilon_k^q\quad\mbox{for all }k,$

and the sequence {ε_k} converges to zero with order q according to the above "simple" definition. To distinguish it from that definition, this is sometimes called R-linear convergence, R-quadratic convergence, etc. (with the R standing for "root").

Examples

Consider the following sequences:

$\begin{align} a_0 &= 1 ,\, &&a_1 = \frac12 ,\, &&a_2 = \frac14 ,\, &&a_3 = \frac18 ,\, &&a_4 = \frac1{16} ,\, &&a_5 = \frac1{32} ,\, &&\ldots ,\, &&a_k = \frac1{2^k} ,\, &&\ldots \\ b_0 &= 1 ,\, &&b_1 = 1 ,\, &&b_2 = \frac14 ,\, &&b_3 = \frac14 ,\, &&b_4 = \frac1{16} ,\, &&b_5 = \frac1{16} ,\, &&\ldots ,\, &&b_k = \frac1{4^{\left\lfloor \frac{k}{2} \right\rfloor}} ,\, &&\ldots \\ c_0 &= \frac12 ,\, &&c_1 = \frac14 ,\, &&c_2 = \frac1{16} ,\, &&c_3 = \frac1{256} ,\, &&c_4 = \frac1{65\,536} ,\, &&&&\ldots ,\, &&c_k = \frac1{2^{2^k}} ,\, &&\ldots \\ d_0 &= 1 ,\, &&d_1 = \frac12 ,\, &&d_2 = \frac13 ,\, &&d_3 = \frac14 ,\, &&d_4 = \frac15 ,\, &&d_5 = \frac16 ,\, &&\ldots ,\, &&d_k = \frac1{k+1} ,\, &&\ldots \end{align}$

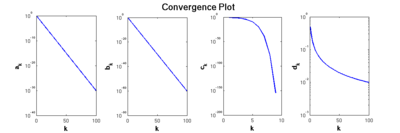
The sequence {a_k} converges linearly to 0 with rate 1/2. More generally, the sequence Cμ^k converges linearly with rate μ if |μ| < 1. The sequence {b_k} also converges linearly to 0 with rate 1/2 under the extended definition, but not under the simple definition. The sequence {c_k} converges superlinearly. In fact, it is quadratically convergent. Finally, the sequence {d_k} converges sublinearly.

Linear, Linear, Superlinear/Quadratic and sublinear rate of convergence.

Convergence speed for discretization methods

A similar situation exists for discretization methods. Here, the important parameter is not the iteration number k but the number of grid points, here denoted n. In the simplest situation (a uniform one-dimensional grid), the number of grid points is inversely proportional to the grid spacing.

In this case, a sequence x_n is said to converge to L with order p if there exists a constant C such that

| x_n − L | < Cn ^{− p} for all n.

This is written as |x_n - L| = O(n^-p) using the big O notation.

This is the relevant definition when discussing methods for numerical quadrature or the solution of ordinary differential equations.

Examples

The sequence {d_k} with d_k = 1 / (k+1) was introduced above. This sequence converges with order 1 according to the convention for discretization methods.

The sequence {a_k} with a_k = 2^-k, which was also introduced above, converges with order p for every number p. It is said to converge exponentially using the convention for discretization methods. However, it only converges linearly (that is, with order 1) using the convention for iterative methods.

Acceleration of convergence

Many methods exist to increase the rate of convergence of a given sequence, i.e. to transform a given sequence into one converging faster to the same limit. Such techniques are in general known as "series acceleration". The goal of the transformed sequence is to be much less "expensive" to calculate than the original sequence. One example of series acceleration is Aitken's delta-squared process.

References

The simple definition is used in

• Michelle Schatzman (2002), Numerical analysis: a mathematical introduction, Clarendon Press, Oxford. ISBN 0-19-850279-6.

The extended definition is used in

• Kendell A. Atkinson (1988), An introduction to numerical analysis (2nd ed.), John Wiley and Sons. ISBN 0-471-50023-2.
• Walter Gautschi (1997), Numerical analysis: an introduction, Birkhäuser, Boston. ISBN 0-817-63895-4.
• Endre Süli and David Mayers (2003), An introduction to numerical analysis, Cambridge University Press. ISBN 0-521-00794-1.

Logarithmic convergence is used in

• Van Tuyl, Andrew H. (1994). "Acceleration of convergence of a family of logarithmically convergent sequences". Mathematics of Computation 63 (207): 229–246. http://www.ams.org/journals/mcom/1994-63-207/S0025-5718-1994-1234428-2/S0025-5718-1994-1234428-2.pdf. 

The Big O definition is used in

• Richard L. Burden and J. Douglas Faires (2001), Numerical Analysis (7th ed.), Brooks/Cole. ISBN 0-534-38216-9

The terms Q-linear and R-linear are used in; The Big O definition when using Taylor series is used in

• Nocedal, Jorge; Wright, Stephen J. (2006). Numerical Optimization (2nd ed.). Berlin, New York: Springer-Verlag. pp. 619+620. ISBN 978-0-387-30303-1 .

One may also study the following paper for Q-linear and R-linear:

• Potra, F. A. (1989). "On Q-order and R-order of convergence". J. Optim. Th. Appl. 63 (3): 415–431. doi:10.1007/BF00939805.