- Chronology of computation of π
-
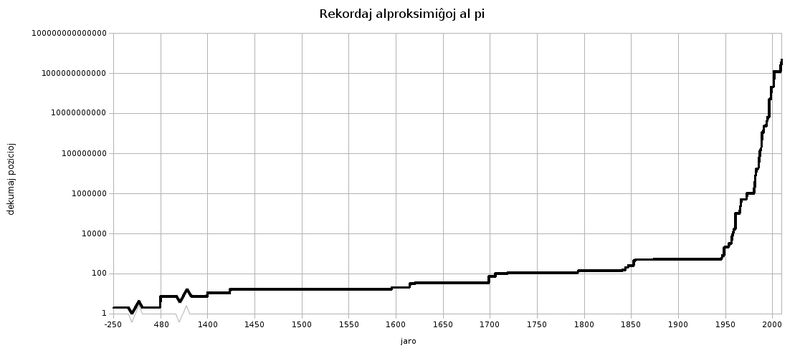
The table below is a brief chronology of computed numerical values of, or bounds on, the mathematical constant pi (π). See the history of numerical approximations of pi for explanations, comments and details concerning some of the calculations mentioned below.Date Who Value of pi
(world records in bold)26th century BC Egyptian Great Pyramid of Giza and Meidum Pyramid[1] 3+1/7 = 22/7 20th century BC Egyptian Rhind Mathematical Papyrus and Moscow Mathematical Papyrus (16/9)2 = 3.160493... 19th century BC Babylonian mathematicians 25/8 = 3.125 9th century BC Indian Shatapatha Brahmana 339/108 = 3.138888... 434 BC Anaxagoras attempted to square the circle with compass and straightedge c. 250 BC Archimedes 223/71 < π < 22/7
(3.140845... < π < 3.142857...)20 BC Vitruvius 25/8 = 3.125 5 Liu Xin 3.154 130 Zhang Heng √10 = 3.162277... 150 Ptolemy 377/120 = 3.141666... 250 Wang Fan 142/45 = 3.155555... 263 Liu Hui 3.141024 480 Zu Chongzhi 3.1415926 < π < 3.1415927 499 Aryabhata 62832/20000 = 3.1416 640 Brahmagupta √10 = 3.162277... 800 Al Khwarizmi 3.1416 1150 Bhāskara II 3.14156 1220 Fibonacci 3.141818 All records from 1400 onwards are given as the number of correct decimal places. 1400 Madhava of Sangamagrama discovered the infinite power series expansion of π, now known as the Leibniz formula for pi 11 decimal places
13 decimal places1424 Jamshīd al-Kāshī 16 decimal places 1573 Valentinus Otho (355/113) 6 decimal places 1593 François Viète 9 decimal places 1593 Adriaen van Roomen 15 decimal places 1596 Ludolph van Ceulen 20 decimal places 1615 32 decimal places 1621 Willebrord Snell (Snellius), a pupil of Van Ceulen 35 decimal places 1665 Isaac Newton 16 decimal places 1681 Takakazu Seki[2] 11 decimal places
16 decimal places1699 Abraham Sharp 71 decimal places 1706 John Machin 100 decimal places 1706 William Jones introduced the Greek letter 'π' 1719 Thomas Fantet de Lagny calculated 127 decimal places, but not all were correct 112 decimal places 1722 Toshikiyo Kamata 24 decimal places 1722 Katahiro Takebe 41 decimal places 1739 Yoshisuke Matsunaga 51 decimal places 1748 Leonhard Euler used the Greek letter 'π' in his book Introductio in Analysin Infinitorum and assured its popularity. 1761 Johann Heinrich Lambert proved that π is irrational 1775 Euler pointed out the possibility that π might be transcendental 1794 Jurij Vega calculated 140 decimal places, but not all are correct 137 decimal places 1794 Adrien-Marie Legendre showed that π² (and hence π) is irrational, and mentioned the possibility that π might be transcendental. 1841 William Rutherford calculated 208 decimal places, but not all were correct 152 decimal places 1844 Zacharias Dase and Strassnitzky calculated 205 decimal places, but not all were correct 200 decimal places 1847 Thomas Clausen calculated 250 decimal places, but not all were correct 248 decimal places 1853 Lehmann 261 decimal places 1853 William Rutherford 440 decimal places 1855 Richter 500 decimal places 1874 William Shanks took 15 years to calculate 707 decimal places but not all were correct (the error was found by D. F. Ferguson in 1946) 527 decimal places 1882 Lindemann proved that π is transcendental (the Lindemann-Weierstrass theorem) 1897 The U.S. state of Indiana came close to legislating the value of 3.2 (among others) for π. House Bill No. 246 passed unanimously. The bill stalled in the state Senate due to a suggestion of possible commercial motives involving publication of a textbook.[3] 1910 Srinivasa Ramanujan finds several rapidly converging infinite series of π, which can compute 8 decimal places of π with each term in the series. Since the 1980s, his series have become the basis for the fastest algorithms currently used by Yasumasa Kanada and the Chudnovsky brothers to compute π. 1946 D. F. Ferguson (using a desk calculator) 620 decimal places 1947 Ivan Niven gave a very elementary proof that π is irrational January 1947 D. F. Ferguson (using a desk calculator) 710 decimal places September 1947 D. F. Ferguson (using a desk calculator) 808 decimal places 1949 D. F. Ferguson and John Wrench, using a desk calculator 1,120 decimal places All records from 1949 onwards were calculated with electronic computers. 1949 John W. Wrench, Jr, and L. R. Smith were the first to use an electronic computer (the ENIAC) to calculate π (it took 70 hours) (also attributed to Reitwiesner et al.) [4] 2,037 decimal places 1953 Kurt Mahler showed that π is not a Liouville number 1954 S. C. Nicholson & J. Jeenel, using the NORC (it took 13 minutes) [5] 3,092 decimal places 1957 G. E. Felton, using the Ferranti Pegasus computer (London) [6] 7,480 decimal places January 1958 Francois Genuys, using an IBM 704 (1.7 hours) [7] 10,000 decimal places May 1958 G. E. Felton, using the Pegasus computer (London) (33 hours) 10,020 decimal places 1959 Francois Genuys, using the IBM 704 (Paris) (4.3 hours) [8] 16,167 decimal places 1961 IBM 7090 (London) (39 minutes) 20,000 decimal places 1961 Daniel Shanks and John Wrench, using the IBM 7090 (New York) (8.7 hours) [9] 100,265 decimal places 1966 Jean Guilloud and J. Filliatre, using the IBM 7030 (Paris) (taking 28 hours??) 250,000 decimal places 1967 Jean Guilloud and M. Dichampt, using the CDC 6600 (Paris) (28 hours) 500,000 decimal places 1973 Jean Guilloud and Martin Bouyer, using the CDC 7600 1,001,250 decimal places 1981 Yasumasa Kanada and Kazunori Miyoshi, FACOM M-200 2,000,036 decimal places 1981 Jean Guilloud, Not known 2,000,050 decimal places 1982 Yoshiaki Tamura, MELCOM 900II 2,097,144 decimal places 1982 Yasumasa Kanada, Yoshiaki Tamura, HITAC M-280H 4,194,288 decimal places 1982 Yasumasa Kanada, Yoshiaki Tamura, HITAC M-280H 8,388,576 decimal places 1983 Yasumasa Kanada, Yoshiaki Tamura, S. Yoshino, HITAC M-280H 16,777,206 decimal places October 1983 Yasumasa Kanada and Yasunori Ushiro, HITAC S-810/20 10,013,395 decimal places October 1985 Bill Gosper, Symbolics 3670 17,526,200 decimal places January 1986 David H. Bailey, CRAY-2 29,360,111 decimal places September 1986 Yasumasa Kanada, Yoshiaki Tamura, HITAC S-810/20 33,554,414 decimal places October 1986 Yasumasa Kanada, Yoshiaki Tamura, HITAC S-810/20 67,108,839 decimal places January 1987 Yasumasa Kanada, Yoshiaki Tamura, Yoshinobu Kubo, NEC SX-2 134,214,700 decimal places January 1988 Yasumasa Kanada and Yoshiaki Tamura, HITAC S-820/80 201,326,551 decimal places May 1989 Gregory V. Chudnovsky & David V. Chudnovsky, CRAY-2 & IBM 3090/VF 480,000,000 decimal places June 1989 Gregory V. Chudnovsky & David V. Chudnovsky, IBM 3090 535,339,270 decimal places July 1989 Yasumasa Kanada and Yoshiaki Tamura, HITAC S-820/80 536,870,898 decimal places August 1989 Gregory V. Chudnovsky & David V. Chudnovsky, IBM 3090 1,011,196,691 decimal places 19 November 1989 Yasumasa Kanada and Yoshiaki Tamura, HITAC S-820/80 1,073,740,799 decimal places August 1991 Gregory V. Chudnovsky & David V. Chudnovsky, Home made parallel computer (details unknown, not verified) [10] 2,260,000,000 decimal places 18 May 1994 Gregory V. Chudnovsky & David V. Chudnovsky, New home made parallel computer (details unknown, not verified) 4,044,000,000 decimal places 26 June 1995 Yasumasa Kanada and Daisuke Takahashi (mathematician), HITAC S-3800/480 (dual CPU) [11] 3,221,220,000 decimal places 28 August 1995 Yasumasa Kanada and Daisuke Takahashi (mathematician), HITAC S-3800/480 (dual CPU) [12] 4,294,960,000 decimal places 11 October 1995 Yasumasa Kanada and Daisuke Takahashi (mathematician), HITAC S-3800/480 (dual CPU) [13] 6,442,450,000 decimal places 6 July 1997 Yasumasa Kanada and Daisuke Takahashi (mathematician), HITACHI SR2201 (1024 CPU) [14] 51,539,600,000 decimal places 5 April 1999 Yasumasa Kanada and Daisuke Takahashi (mathematician), HITACHI SR8000 (64 of 128 nodes) [15] 68,719,470,000 decimal places 20 September 1999 Yasumasa Kanada and Daisuke Takahashi (mathematician), HITACHI SR8000/MPP (128 nodes) [16] 206,158,430,000 decimal places 24 November 2002 Professor Yasumasa Kanada & 9 man team, HITACHI SR8000/MPP (64 nodes), 600 hours, Department of Information Science at the University of Tokyo in Tokyo, Japan [17] 1,241,100,000,000 decimal places 29 April 2009 Professor Daisuke Takahashi (mathematician) et al., T2K Open Supercomputer (640 nodes), single node speed is 147.2 gigaflops, 29.09 hours, computer memory is 13.5 terabytes, Gauss–Legendre algorithm, Center for Computational Sciences at the University of Tsukuba in Tsukuba, Japan[18] 2,576,980,377,524 decimal places All records from Dec 2009 onwards are calculated on home computers with commercially available parts. 31 December 2009 Fabrice Bellard - Core i7 CPU at 2.93 GHz
- 6 GiB (1) of RAM
- 7.5 TB of disk storage using five 1.5 TB hard disks (Seagate Barracuda 7200.11 model)
- 64 bit Red Hat Fedora 10 distribution
- Computation of the binary digits: 103 days
- Verification of the binary digits: 13 days
- Conversion to base 10: 12 days
- Verification of the conversion: 3 days
- 131 days in total - The verification of the binary digits used a network of 9 Desktop PCs during 34 hours, Chudnovsky algorithm, see [19] for Bellard's homepage.[20]
2,699,999,990,000 decimal places 2 August 2010 Shigeru Kondo[21] - using y-cruncher[22] by Alexander Yee
- the Chudnovsky formula was used for main computation
- verification used the Bellard & Plouffe formulas on different computers, both computed 32 hexadecimal digits ending with the 4,152,410,118,610th.
- with 2 x Intel Xeon X5680 @ 3.33 GHz - (12 physical cores, 24 hyperthreaded)
- 96 GB DDR3 @ 1066 MHz - (12 x 8 GB - 6 channels) - Samsung (M393B1K70BH1)
- 1 TB SATA II (Boot drive) - Hitachi (HDS721010CLA332), 3 x 2 TB SATA II (Store Pi Output) - Seagate (ST32000542AS) 16 x 2 TB SATA II (Computation) - Seagate (ST32000641AS)
- Windows Server 2008 R2 Enterprise x64
- Computation of binary digits: 80 days
- Conversion to base 10: 8.2 days
- Verification of the conversion: 45.6 hours
- Verification of the binary digits: 64 hours (primary), 66 hours (secondary)
- Total Time: 90 days - The verification of the binary digits were done simultaneously on two separate computers during the main computation.[23]
5,000,000,000,000 decimal places 17 October 2011 Shigeru Kondo[24] - using y-cruncher by Alexander Yee
- Computation: 371 days
- Verification: 1.86 days and 4.94 days
- Total time: 371 days
10,000,000,000,000 decimal places See also
Part of a series of articles on the mathematical constant π 
Uses Area of disk · Circumference
Use in other formulaeProperties Irrationality · Transcendence
Less than 22/7Value Approximations · Memorization People Archimedes · Liu Hui · Zu Chongzhi
Madhava of Sangamagrama
William Jones · John Machin
John Wrench · Ludolph van CeulenHistory Chronology · Book In culture Legislation · Holiday Related topics Squaring the circle · Basel problem
Tau (τ) · Other topics related to π- History of pi
References
- ^ Petrie, W.M.F. Surveys of the Great Pyramids. Nature Journal: 942-943. 1925
- ^ Yoshio, Mikami; Eugene Smith, David (April 2004) [1914]. A History of Japanese Mathematics (paperback ed.). Dover Publications. ISBN 0486434826. http://www.archive.org/details/historyofjapanes00smitiala.
- ^ Lopez-Ortiz, Alex (February 20, 1998). "Indiana Bill sets value of Pi to 3". the news.answers WWW archive. Department of Information and Computing Sciences, Utrecht University. http://www.cs.uu.nl/wais/html/na-dir/sci-math-faq/indianabill.html. Retrieved 2009-02-01.
- ^ G. Reitwiesner, "An ENIAC determination of Pi and e to more than 2000 decimal places," MTAC, v. 4, 1950, p. 11-15"
- ^ S. C, Nicholson & J. Jeenel, "Some comments on a NORC computation of x," MTAC, v. 9, 1955, p. 162-164
- ^ G. E. Felton, "Electronic computers and mathematicians," Abbreviated Proceedings of the Oxford Mathematical Conference for Schoolteachers and Industrialists at Trinity College, Oxford, April 8–18, 1957, p. 12-17, footnote p. 12-53. This published result is correct to only 7480D, as was established by Felton in a second calculation, using formula (5), completed in 1958 but apparently unpublished. For a detailed account of calculations of x see J. W. Wrench, Jr., "The evolution of extended decimal approximations to x," The Mathematics Teacher, v. 53, 1960, p. 644-650
- ^ F. Genuys, "Dix milles decimales de x," Chiffres, v. 1, 1958, p. 17-22.
- ^ This unpublished value of x to 16167D was computed on an IBM 704 system at the Commissariat à l'Energie Atomique in Paris, by means of the program of Genuys
- ^ [1] "Calculation of Pi to 100,000 Decimals" in the journal Mathematics of Computation, vol 16 (1962), issue 77, page 76-99.
- ^ Bigger slices of Pi (determination of the numerical value of pi reaches 2.16 billion decimal digits) Science News 24 August 1991 http://www.encyclopedia.com/doc/1G1-11235156.html
- ^ ftp://pi.super-computing.org/README.our_last_record_3b
- ^ ftp://pi.super-computing.org/README.our_last_record_4b
- ^ ftp://pi.super-computing.org/README.our_last_record_6b
- ^ ftp://pi.super-computing.org/README.our_last_record_51b
- ^ ftp://pi.super-computing.org/README.our_last_record_68b
- ^ ftp://pi.super-computing.org/README.our_latest_record_206b
- ^ http://www.super-computing.org/pi_current.html
- ^ http://www.hpcs.is.tsukuba.ac.jp/~daisuke/pi.html
- ^ http://bellard.org
- ^ http://bellard.org/pi/pi2700e9/pipcrecord.pdf
- ^ Shigeru Kondo
- ^ y-cruncher - A Multi-Threaded Pi-Program
- ^ Kondo's 2010 record, A. Yee's program y-cruncher
- ^ Pi - 10 Trillion Digits
External links
- Borwein, Jonathan, "The Life of Pi"
- Stu's Pi page
- Takahashi's page
Categories:
Wikimedia Foundation. 2010.