- Squaring the circle
-
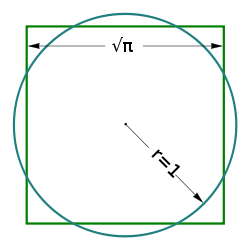
Squaring the circle: the areas of this square and this circle are equal. In 1882, it was proven that this figure cannot be constructed in a finite number of steps with an idealized compass and straightedge.Some apparent partial solutions gave false hope for a long time. In this figure, the shaded figure is the Lune of Hippocrates. Its area is equal to the area of the triangle ABC (found by Hippocrates of Chios).
Part of a series of articles on the mathematical constant π 
Uses Area of disk · Circumference
Use in other formulaeProperties Irrationality · Transcendence
Less than 22/7Value Approximations · Memorization People Archimedes · Liu Hui · Zu Chongzhi
Madhava of Sangamagrama
William Jones · John Machin
John Wrench · Ludolph van CeulenHistory Chronology · Book In culture Legislation · Holiday Related topics Squaring the circle · Basel problem
Tau (τ) · Other topics related to πSquaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the same area as a given circle by using only a finite number of steps with compass and straightedge. More abstractly and more precisely, it may be taken to ask whether specified axioms of Euclidean geometry concerning the existence of lines and circles entail the existence of such a square.
In 1882, the task was proven to be impossible, as a consequence of the Lindemann–Weierstrass theorem which proves that pi (π) is a transcendental, rather than an algebraic irrational number; that is, it is not the root of any polynomial with rational coefficients. It had been known for some decades before then that if pi were transcendental then the construction would be impossible, but that pi is transcendental was not proven until 1882. Approximate squaring to any given non-perfect accuracy, in contrast, is possible in a finite number of steps, since there are rational numbers arbitrarily close to pi.
The expression "squaring the circle" is sometimes used as a metaphor for doing something logically or intuitively impossible.
The term quadrature of the circle is sometimes used synonymously, or may refer to approximate or numerical methods for finding the area of a circle.
Contents
History
Methods to approximate the area of a given circle with a square were known already to Babylonian mathematicians. The Egyptian Rhind papyrus of 1800BC gives the area of a circle as (64/81) d 2, where d is the diameter of the circle, and pi approximated to 256/81, a number that appears in the older Moscow Mathematical Papyrus, and used for volume approximations (i.e. hekat (volume unit)). Indian mathematicians also found an approximate method, though less accurate, documented in the Sulba Sutras.[1] Archimedes showed that the value of pi lay between 3 + 1/7 (approximately 3.1429) and 3 + 10/71 (approximately 3.1408). See Numerical approximations of π for more on the history.
The first Greek to be associated with the problem was Anaxagoras, who worked on it while in prison. Hippocrates of Chios squared certain lunes, in the hope that it would lead to a solution — see Lune of Hippocrates. Antiphon the Sophist believed that inscribing regular polygons within a circle and doubling the number of sides will eventually fill up the area of the circle, and since a polygon can be squared, it means the circle can be squared. Even then there were skeptics—Eudemus argued that magnitudes cannot be divided up without limit, so the area of the circle will never be used up.[2] The problem was even mentioned in Aristophanes's play The Birds.
It is believed that Oenopides was the first Greek who required a plane solution (that is, using only a compass and straightedge). James Gregory attempted a proof of its impossibility in Vera Circuli et Hyperbolae Quadratura (The True Squaring of the Circle and of the Hyperbola) in 1667. Although his proof was incorrect, it was the first paper to attempt to solve the problem using algebraic properties of pi. It was not until 1882 that Ferdinand von Lindemann rigorously proved its impossibility.
The famous Victorian-age mathematician, logician and author, Charles Lutwidge Dodgson (better known under the pseudonym, "Lewis Carroll") also expressed interest in debunking illogical circle-squaring theories. In one of his diary entries for 1855, Dodgson listed books he hoped to write including one called "Plain Facts for Circle-Squarers". In the introduction to "A New Theory of Parallels", Dodgson recounted an attempt to demonstrate logical errors to a couple of circle-squarers, stating:[4]
"The first of these two misguided visionaries filled me with a great ambition to do a feat I have never heard of as accomplished by man, namely to convince a circle squarer of his error! The value my friend selected for Pi was 3.2: the enormous error tempted me with the idea that it could be easily demonstrated to BE an error. More than a score of letters were interchanged before I became sadly convinced that I had no chance."
Impossibility
The solution of the problem of squaring the circle by compass and straightedge demands construction of the number
 , and the impossibility of this undertaking follows from the fact that pi is a transcendental (non-algebraic and therefore non-constructible) number. If the problem of the quadrature of the circle is solved using only compass and straightedge, then an algebraic value of pi would be found, which is impossible. Johann Heinrich Lambert conjectured that pi was transcendental in 1768 in the same paper he proved its irrationality, even before the existence of transcendental numbers was proven. It was not until 1882 that Ferdinand von Lindemann proved its transcendence.
, and the impossibility of this undertaking follows from the fact that pi is a transcendental (non-algebraic and therefore non-constructible) number. If the problem of the quadrature of the circle is solved using only compass and straightedge, then an algebraic value of pi would be found, which is impossible. Johann Heinrich Lambert conjectured that pi was transcendental in 1768 in the same paper he proved its irrationality, even before the existence of transcendental numbers was proven. It was not until 1882 that Ferdinand von Lindemann proved its transcendence.The transcendence of pi implies the impossibility of exactly "circling" the square, as well as of squaring the circle.
It is possible to construct a square with an area arbitrarily close to that of a given circle. If a rational number is used as an approximation of pi, then squaring the circle becomes possible, depending on the values chosen. However, this is only an approximation and does not meet the constraints of the ancient rules for solving the problem. Several mathematicians have demonstrated workable procedures based on a variety of approximations.
Bending the rules by allowing an infinite number of compass-and-straightedge operations or by performing the operations on certain non-Euclidean spaces also makes squaring the circle possible. For example, although the circle cannot be squared in Euclidean space, it can be in Gauss–Bolyai–Lobachevsky space. Indeed, even the preceding phrase is overoptimistic.[5][6] There are no squares as such in the hyperbolic plane, although there are regular quadrilaterals, meaning quadrilaterals with all sides congruent and all angles congruent (but these angles are strictly smaller than right angles). There exist, in the hyperbolic plane, (countably) infinitely many pairs of constructible circles and constructible regular quadrilaterals of equal area. However, there is no method for starting with a regular quadrilateral and constructing the circle of equal area, and there is no method for starting with a circle and constructing a regular quadrilateral of equal area (even when the circle has small enough radius such that a regular quadrilateral of equal area exists).
Modern approximative constructions
Though squaring the circle is an impossible problem using only compass and straightedge, approximations to squaring the circle can be given by constructing lengths close to pi. It takes only minimal knowledge of elementary geometry to convert any given rational approximation of pi into a corresponding compass-and-straightedge construction, but constructions made in this way tend to be very long-winded in comparison to the accuracy they achieve. After the exact problem was proven unsolvable, some mathematicians applied their ingenuity to finding elegant approximations to squaring the circle, defined roughly (and informally) as constructions that are particularly simple among other imaginable constructions that give similar precision.
Among the modern approximate constructions was one by E. W. Hobson in 1913 (see his book[7]). This was a fairly accurate construction which was based on constructing the approximate value of 3.14164079..., which is accurate to 4 decimals (i.e. it differs from pi by about 4.8×10−5).
Indian mathematician Srinivasa Ramanujan in 1913, C. D. Olds in 1963, Martin Gardner in 1966, and Benjamin Bold in 1982 all gave geometric constructions for
which is accurate to six decimal places of pi.
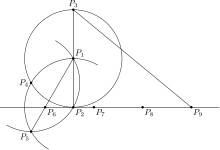 Kochański's approximate construction
Kochański's approximate construction
Srinivasa Ramanujan in 1914 gave a ruler-and-compass construction which was equivalent to taking the approximate value for pi to be
giving a remarkable eight decimal places of pi.
In 1991, Robert Dixon gave constructions for
(Kochański's approximation), though these were only accurate to four decimal places of pi.
Squaring or quadrature as integration
The problem of finding the area under a curve, known as integration in calculus, or quadrature in numerical analysis, was known as squaring before the invention of calculus. Since the techniques of calculus were unknown, it was generally presumed that a squaring should be done via geometric constructions, that is, by compass and straightedge. For example Newton wrote to Oldenberg in 1676 "I believe M. Leibnitz will not dislike the Theorem towards the beginning of my letter pag. 4 for squaring Curve lines Geometrically" (emphasis added).[8] After Newton and Leibniz invented calculus, they still referred to this integration problem as squaring a curve.
"Squaring the circle" as a metaphor
The futility of exercises aimed at finding the quadrature of the circle has lent itself to metaphors describing a hopeless, meaningless, or vain undertaking.
For example, in Spanish, the expression "descubriste la cuadratura del círculo" ("you discovered the quadrature of the circle") is often used derisively to dismiss claims that someone has found a simple solution to a particularly hard or intractable problem.[citation needed]
Claims of circle squaring, and the longitude problem
The mathematical proof that the quadrature of the circle is impossible using only compass and straightedge has not proved to be a hindrance to the many people who have invested years in this problem anyway. Having squared the circle is a famous crank assertion. (See also pseudomathematics.) In his old age, the English philosopher Thomas Hobbes convinced himself that he had succeeded in squaring the circle.
During the 18th and 19th century the notion that the problem of squaring the circle was somehow related to the longitude problem seems to have become prevalent among would-be circle squarers. Using "cyclometer" for circle-squarer, Augustus de Morgan wrote in 1872:
Montucla says, speaking of France, that he finds three notions prevalent among cyclometers: 1. That there is a large reward offered for success; 2. That the longitude problem depends on that success; 3. That the solution is the great end and object of geometry. The same three notions are equally prevalent among the same class in England. No reward has ever been offered by the government of either country.[9]
Although from 1714 to 1828 the British government did indeed sponsor a £20,000 prize for finding a solution to the longitude problem, exactly why the connection was made to squaring the circle is not clear; especially since two non-geometric methods (the astronomical method of lunar distances and the mechanical chronometer) had been found by the late 1760s. De Morgan goes on to say that "[t]he longitude problem in no way depends upon perfect solution; existing approximations are sufficient to a point of accuracy far beyond what can be wanted." In his book, de Morgan also mentions receiving many threatening letters from would-be circle squarers, accusing him of trying to "cheat them out of their prize."
See also
- The two other classical problems of antiquity were doubling the cube and "trisecting the angle", described in the compass and straightedge article. Unlike squaring the circle, these two problems can be solved by the slightly more powerful construction method of origami, as described at mathematics of paper folding.
- For a more modern related problem, see Tarski's circle-squaring problem.
- The Indiana Pi Bill, an 1897 attempt by the Indiana state legislature to dictate a solution to the problem by legislative fiat.
- Squircle, a mathematical shape with properties between those of a square and those of a circle.
- La Quadrature du Net, a digital-rights advocacy group.
References
- ^ O'Connor, John J. and Robertson, Edmund F. (2000). The Indian Sulbasutras, MacTutor History of Mathematics archive, St Andrews University.
- ^ Heath, Thomas (1981). History of Greek Mathematics. Courier Dover Publications. ISBN 0486240746.
- ^ Florian Cajori, A History of Mathematics, second edition, p. 143, New York: The Macmillan Company, 1919.
- ^ Martin Gardner (1996). The Universe in a Handkerchief. Springer. ISBN 038794673X.
- ^ Jagy, William C. (1995). "Squaring circles in the hyperbolic plane" (PDF). Mathematical Intelligencer 17 (2): 31–36. doi:10.1007/BF03024895. http://zakuski.math.utsa.edu/~jagy/papers/Intelligencer_1995.pdf
- ^ Greenberg, Marvin Jay (2008). Euclidean and Non-Euclidean Geometries (Fourth ed.). W H Freeman. pp. 520–528. ISBN 0-7167-9948-0
- ^ Hobson, Ernest William (1913). Squaring the Circle: A History of the Problem, Cambridge University Press. Reprinted by Merchant Books in 2007.
- ^ [1]
- ^ Augustus de Morgan (1872) A Budget of Paradoxes, p. 96.
External links
- Squaring the circle at the MacTutor History of Mathematics archive
- Squaring the Circle at cut-the-knot
- Circle Squaring at MathWorld, includes information on procedures based on various approximations of pi
- "Squaring the Circle" at "Convergence"
- The Quadrature of the Circle and Hippocrates' Lunes at Convergence
- How to Unroll a Circle Pi accurate to eight decimal places, using straightedge and compass.
- Squaring the Circle and Other Impossibilities, lecture by Robin Wilson, at Gresham College, 16 January 2008 (available for download as text, audio or video file).
Greek mathematics Mathematicians Anaxagoras · Anthemius · Archytas · Aristaeus the Elder · Aristarchus · Apollonius · Archimedes · Autolycus · Bion · Boethius · Bryson · Callippus · Carpus · Chrysippus · Cleomedes · Conon · Ctesibius · Democritus · Dicaearchus · Diocles · Diophantus · Dinostratus · Dionysodorus · Domninus · Eratosthenes · Eudemus · Euclid · Eudoxus · Eutocius · Geminus · Heron · Hipparchus · Hippasus · Hippias · Hippocrates · Hypatia · Hypsicles · Isidore of Miletus · Leo the Mathematician · Marinus · Melissa · Menaechmus · Menelaus · Metrodorus · Nicomachus · Nicomedes · Nicoteles · Oenopides · Pappus · Perseus · Philolaus · Philon · Porphyry · Posidonius · Proclus · Ptolemy · Pythagoras · Serenus · Simplicius · Sosigenes · Sporus · Thales · Theaetetus · Theano · Themistoclea · Theodorus · Theodosius · Theon of Alexandria · Theon of Smyrna · Thymaridas · Xenocrates · Zeno of Elea · Zeno of Sidon · ZenodorusTreatises Centers Influences Influenced Tables Problems Categories:- Pi
- Euclidean plane geometry
- Mathematical problems
- History of geometry
Wikimedia Foundation. 2010.




![\left(9^2 + \frac{19^2}{22}\right)^{1/4} = \sqrt[4]{\frac{2143}{22}} = 3.1415926525826461252\dots](f/baf1a09003c20516c6db779602fe9b94.png)
