Periodic function

Not to be confused with periodic mapping, a mapping whose nth iterate is the identity (see periodic point).

In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations, waves, and other phenomena that exhibit periodicity. Any function which is not periodic is called aperiodic.

An illustration of a periodic function with period P.

Definition

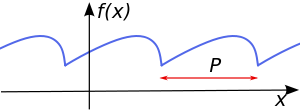
A function f is said to be periodic with period P if (for some nonzero constant P) we have

$f(x+P) = f(x) \,\!$

for all values of x. If there exists a least positive^[1] constant P with this property, it is called the prime period. A function with period P will repeat on intervals of length P, and these intervals are sometimes also referred to as periods.

Geometrically, a periodic function can be defined as a function whose graph exhibits translational symmetry. Specifically, a function f is periodic with period P if the graph of f is invariant under translation in the x-direction by a distance of P. This definition of periodic can be extended to other geometric shapes and patterns, such as periodic tessellations of the plane.

A function that is not periodic is called aperiodic.

Examples

A graph of the sine function, showing two complete periods.

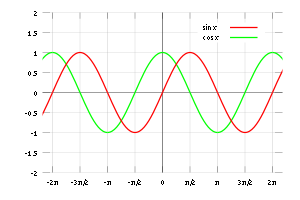
For example, the sine function is periodic with period 2π, since

$\sin(x + 2\pi) = \sin(x) \,\!$

for all values of x. This function repeats on intervals of length 2π (see the graph to the right).

Everyday examples are seen when the variable is time; for instance the hands of a clock or the phases of the moon show periodic behaviour. Periodic motion is motion in which the position(s) of the system are expressible as periodic functions, all with the same period.

For a function on the real numbers or on the integers, that means that the entire graph can be formed from copies of one particular portion, repeated at regular intervals.

A simple example of a periodic function is the function f that gives the "fractional part" of its argument. Its period is 1. In particular,

f( 0.5 ) = f( 1.5 ) = f( 2.5 ) = ... = 0.5.

The graph of the function f is the sawtooth wave.

A plot of f(x) = sin(x) and g(x) = cos(x); both functions are periodic with period 2π.

The trigonometric functions sine and cosine are common periodic functions, with period 2π (see the figure on the right). The subject of Fourier series investigates the idea that an 'arbitrary' periodic function is a sum of trigonometric functions with matching periods.

According to the definition above, some exotic functions, for example the Dirichlet function, are also periodic; in the case of Dirichlet function, any nonzero rational number is a period.

Properties

If a function f is periodic with period P, then for all x in the domain of f and all integers n,

f(x + nP) = f(x).

If f(x) is a function with period P, then f(ax+b), where a is a positive constant, is periodic with period P/a. For example, f(x)=sinx has period 2π, therefore sin(5x) will have period 2π/5.

Double-periodic functions

A function whose domain is the complex numbers can have two incommensurate periods without being constant. The elliptic functions are such functions. ("Incommensurate" in this context means not real multiples of each other.)

Complex example

Using complex variables we have the common period function:

$e^{ikx} = \cos kx + i\,\sin kx$

As you can see, since the cosine and sine functions are periodic, and the complex exponential above is made up of cosine/sine waves, then the above (actually Euler's formula) has the following property. If L is the period of the function then:

L = 2π / k

Generalizations

Antiperiodic functions

One common generalization of periodic functions is that of antiperiodic functions. This is a function f such that f(x + P) = −f(x) for all x. (Thus, a P-antiperiodic function is a 2P-periodic function.)

Bloch-periodic functions

A further generalization appears in the context of Bloch waves and Floquet theory, which govern the solution of various periodic differential equations. In this context, the solution (in one dimension) is typically a function of the form:

$f(x+P) = e^{ikP} f(x) \,\!$

where k is a real or complex number (the Bloch wavevector or Floquet exponent). Functions of this form are sometimes called Bloch-periodic in this context. A periodic function is the special case k = 0, and an antiperiodic function is the special case k = π/P.

Quotient spaces as domain

In signal processing you encounter the problem, that Fourier series represent periodic functions and that Fourier series satisfy convolution theorems (i.e. convolution of Fourier series corresponds to multiplication of represented periodic function and vice versa), but periodic functions cannot be convolved with the usual definition, since the involved integrals diverge. A possible way out is to define a periodic function on a bounded but periodic domain. To this end you can use the notion of a quotient space:

${\mathbb{R}/\mathbb{Z}} = \{x+\mathbb{Z} : x\in\mathbb{R}\} = \{\{y : y\in\mathbb{R}\land y-x\in\mathbb{Z}\} : x\in\mathbb{R}\}$.

That is, each element in ${\mathbb{R}/\mathbb{Z}}$ is an equivalence class of real numbers that share the same fractional part. Thus a function like $f : {\mathbb{R}/\mathbb{Z}}\to\mathbb{R}$ is a representation of a 1-periodic function.

See also

• Periodic sequence
• Almost periodic function
• Amplitude
• Definite pitch
• Doubly periodic function
• Floquet theory
• Frequency
• Oscillation
• Quasiperiodic function
• Wavelength
• Periodic summation

References

1. ^ For some functions, like a constant function or the indicator function of the rational numbers, a least positive "period" may not exist (the infimum of possible positve P being zero).

• Ekeland, Ivar (1990). "One". Convexity methods in Hamiltonian mechanics. Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)]. 19. Berlin: Springer-Verlag. pp. x+247. ISBN 3-540-50613-6. MR1051888. 

External links

• Periodic functions at MathWorld