Chord (geometry)

A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle. A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse. A chord that passes through the circle's center point is the circle's diameter.

The red line BX is a chord
(as is the diameter line AB).

Chords of a circle

Further information: Chord properties

Among properties of chords of a circle are the following:

1. Chords are equidistant from the center only if their lengths are equal.
2. A chord's perpendicular bisector passes through the centre.
3. If the line extensions (secant lines) of chords AB and CD intersect at a point P, then their lengths satisfy AP·PB = CP·PD (power of a point theorem).

The area that a circular chord "cuts off" is called a circular segment.

Chords of an ellipse

The midpoints of a set of parallel chords of an ellipse are collinear.^[1]:p.147

Chords in trigonometry

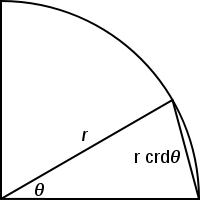
Chords were used extensively in the early development of trigonometry. The first known trigonometric table, compiled by Hipparchus, tabulated the value of the chord function for every 7.5 degrees. Ptolemy of Alexandria compiled a more extensive table of chords in his book on astronomy, giving the value of the chord for angles ranging from 1/2 degree to 180 degrees by increments of half a degree.

The chord function is defined geometrically as in the picture to the left. The chord of an angle is the length of the chord between two points on a unit circle separated by that angle. The chord function can be related to the modern sine function, by taking one of the points to be (1,0), and the other point to be (cos θ, sin θ), and then using the Pythagorean theorem to calculate the chord length:

$\mathrm{crd}\ \theta = \sqrt{(1-\cos \theta)^2+\sin^2 \theta} = \sqrt{2-2\cos \theta} = 2 \sqrt{\frac{1-\cos \theta}{2}} = 2 \sin \frac{\theta}{2}.$

The last step uses the half-angle formula. Much as modern trigonometry is built on the sine function, ancient trigonometry was built on the chord function. Hipparchus is purported to have written a twelve volume work on chords, all now lost, so presumably a great deal was known about them. The chord function satisfies many identities analogous to well-known modern ones:

Name	Sine-based	Chord-based
Pythagorean	$\sin^2 \theta + \cos^2 \theta = 1 \,$	$\mathrm{crd}^2 \theta + \mathrm{crd}^2 (180^\circ - \theta) = 4 \,$
Half-angle	$\sin\frac{\theta}{2} = \pm\sqrt{\frac{1-\cos \theta}{2}} \,$	$\mathrm{crd}\ \frac{\theta}{2} = \pm \sqrt{2-\mathrm{crd}(180^\circ - \theta)} \,$

The half-angle identity greatly expedites the creation of chord tables. Ancient chord tables typically used a large value for the radius of the circle, and reported the chords for this circle. It was then a simple matter of scaling to determine the necessary chord for any circle. According to G. J. Toomer, Hipparchus used a circle of radius 3438' (= 3438/60 = 57.3). This value is extremely close to 180 / π (= 57.29577951...). One advantage of this choice of radius was that he could very accurately approximate the chord of a small angle as the angle itself. In modern terms, it allowed a simple linear approximation:

$\frac{3438}{60} \mathrm{crd}\ \theta = 2 \frac{3438}{60} \sin \frac{\theta}{2} \approx 2 \frac{3438}{60} \frac{\pi}{180} \frac{\theta}{2} = \left(\frac{3438}{60} \frac{\pi}{180}\right) \theta \approx \theta.$

Calculating circular chords

The chord of a circle can be calculated using other information:^[2]

Initial data	Radius (r)	Diameter (D)
Sagitta (s)	$c = 2 \sqrt {s (2 r - s)}$	$c = 2 \sqrt {s (D - s)}$
Apothem (a)	$c=2 \sqrt{r^2- a^2}$	$c=\sqrt{D ^2-4 a^2}$
Angle (θ)	$c=2 r \sin \left(\frac{\theta }{2}\right)$	$c=D \sin \left(\frac{\theta }{2}\right)$

See also

• Circular segment
• Circle graph

References

1. ^ Chakerian, G. D. "A Distorted View of Geometry." Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979.
2. ^ Déplanche, Y.,Diccio fórmulas, 1996, Edunsa (publ.), p. 29. [1], isbn=9788477471196

External links

• History of Trigonometry Outline
• Trigonometric functions, focusing on history
• Chord (of a circle) With interactive animation