- Circular segment
-
In geometry, a circular segment is an area of a circle informally defined as an area which is "cut off" from the rest of the circle by a secant or a chord. The circle segment constitutes the part between the secant and an arc, excluding the circle's center. This is commonly known as Meglio's Area.
Contents
Formulas
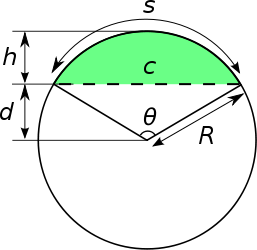
Let R be the radius of the circle, θ is the central angle in radians, α is the central angle in degrees, c the chord length, s the arc length, h the height of the segment, and d the height of the triangular portion.
- The radius is

- The arc length is

- The chord length is

- The height is

- The angle is

Area
The area of the circular segment is equal to the area of the circular sector minus the area of the triangular portion.

It should be noted that theta in this equation is in radians. For theta in degrees the following modification should be added:

Radius
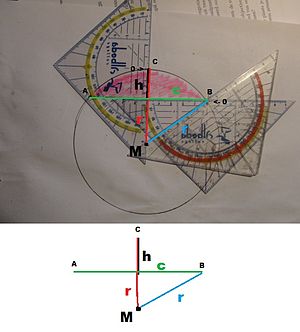
A way of approaching the radius of a Circular segment with only the chord and height of the segment is the Pietrow-Vollema Radius method. This method uses the constant length of the radius of a circle as a way of finding it. One can find the radius by recreating the shape of the included picture, with two or three rulers. Meaning that the first ruler is set to zero on point C, and the other on point B. Then by crossing the rulers one can find the exact point of intersection where both of the rulers have back the same length. Thus the radius of the circle.
This method can also be used to find the angle ½θ of the segment, by measuring the angle between the two above mentioned rulers.
See also
External links
- Weisstein, Eric W., "Circular segment" from MathWorld.
- Definition of a circular segment With interactive animation
- Formulae for area of a circular segment With interactive animation
Categories:- Circles
- The radius is
Wikimedia Foundation. 2010.