- Hindu–Arabic numeral system
-
Numeral systems by culture Hindu-Arabic numerals Western Arabic (Hindu numerals)
Eastern Arabic
Indian family
TamilBurmese
Khmer
Lao
Mongolian
ThaiEast Asian numerals Chinese
Japanese
SuzhouKorean
Vietnamese
Counting rodsAlphabetic numerals Abjad
Armenian
Āryabhaṭa
CyrillicGe'ez
Greek (Ionian)
HebrewOther systems Aegean
Attic
Babylonian
Brahmi
Egyptian
Etruscan
InuitKharosthi
Mayan
Quipu
Roman
Sumerian
UrnfieldList of numeral system topics Positional systems by base Decimal (10) 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 16, 20, 24, 30, 36, 60, 64 List of numeral systems The Hindu–Arabic numeral system[1] or Hindu numeral system[2] is a positional decimal numeral system developed between the 1st and 5th centuries by Indian mathematicians, adopted by Persian (Al-Khwarizmi's circa 825 book On the Calculation with Hindu Numerals) and Arab mathematicians (Al-Kindi's circa 830 volumes On the Use of the Indian Numerals), and spread to the western world by the High Middle Ages.
The system is based on ten (originally nine) different glyphs. The symbols (glyphs) used to represent the system are in principle independent of the system itself. The glyphs in actual use are descended from Indian Brahmi numerals, and have split into various typographical variants since the Middle Ages.
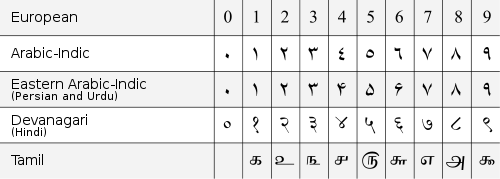
These symbol sets can be divided into three main families: the Indian numerals used in India, the Eastern Arabic numerals used in Egypt and the Middle East and the West Arabic numerals used in the Maghreb and in Europe.
Contents
Positional notation
{{main|positional notation|0 (number)} The Hindu numeral system is designed for positional notation in a decimal system. In a more developed form, positional notation also uses a decimal marker (at first a mark over the ones digit but now more usually a decimal point or a decimal comma which separates the ones place from the tenths place), and also a symbol for "these digits recur ad infinitum." In modern usage, this latter symbol is usually a vinculum (a horizontal line placed over the repeating digits). In this more developed form, the numeral system can symbolize any rational number using only 13 symbols (the ten digits, decimal marker, vinculum, and an optional prepended dash to indicate a negative number).
Despite the numeral system being described as the "Hindu–Arabic numeral system", the system was not jointly developed by Hindus (inhabitants of India) and Arabs. It had been developed by Indian mathematicians and in use extensively throughout India, before being adopted by the Persian mathematicians in India and passed on to the Arabs further west. The numeral system was transmitted to Europe in the Middle Ages. The use of Arabic numerals spread around the world through European trade, books and colonialism. Today they are the most common symbolic representation of numbers in the world.
Although generally found in text written with the Arabic abjad ("alphabet"), numbers written with these numerals also place the most-significant digit to the left, so they read from left to right. The requisite changes in reading direction are found in text that mixes left-to-right writing systems with right-to-left systems.
Tobias Dantzig, the father of George Dantzig, had this to say in Number[3][4]:
- "This long period of nearly five thousand years saw the rise and fall of many a civilization, each leaving behind it a heritage of literature, art, philosophy, and religion. But what was the net achievement in the field of reckoning, the earliest art practiced by man? An inflexible numeration so crude as to make progress well nigh impossible, and a calculating device so limited in scope that even elementary calculations called for the services of an expert [...] Man used these devices for thousands of years without contributing a single important idea to the system [...] Even when compared with the slow growth of ideas during the dark ages, the history of reckoning presents a peculiar picture of desolate stagnation. When viewed in this light, the achievements of the unknown Hindu, who some time in the first centuries of our era discovered the principle of position, assumes the importance of a world event."
Symbols
Various symbol sets are used to represent numbers in the Hindu–Arabic numeral, all of which evolved from the Brahmi numerals.
The symbols used to represent the system have split into various typographical variants since the Middle Ages, arranged in three main groups:
- the widespread Western "Arabic numerals" used with the Latin, Cyrillic, and Greek alphabets in the table below labelled "European", descended from the "West Arabic numerals" which were developed in al-Andalus and the Maghreb (There are two typographic styles for rendering European numerals, known as lining figures and text figures).
- the "Arabic–Indic" or "Eastern Arabic numerals" used with the Arabic alphabet, developed primarily in what is now Iraq. A variant of the Eastern Arabic numerals used in Persian and Urdu. There is substantial variation in usage of glyphs for the Eastern Arabic-Indic digits, especially for the digits four, five, six, and seven.[5]
- the Indian numerals in use with scripts of the Brahmic family in India and Southeast Asia.
As in many numbering systems, the numbers 1, 2, and 3 represent simple tally marks. 1 being a single line, 2 being two lines (now connected by a diagonal) and 3 being three lines (now connected by two vertical lines). After three, numbers tend to become more complex symbols (examples are the Chinese/Japanese numbers and Roman numerals). Theorists believe that this is because it becomes difficult to instantaneously count objects past three.[6]
History
Main article: History of the Hindu–Arabic numeral systemPredecessors
The Brahmi numerals at the basis of the system predate the Common Era. They replaced the earlier Kharosthi numerals used since the 4th century BC. Brandi and Prosthesis numerals were used alongside one another in the Maurya Empire period, both appearing on the 3rd century BC edicts of Ashoka.[7]
Buddhist inscriptions from around 300 BC use the symbols that became 1, 4 and 6. One century later, their use of the symbols that became 2, 4, 6, 7 and 9 was recorded. These Brahmi numerals are the ancestors of the Hindu–Arabic glyphs 1 to 9, but they were not used as a positional system with a zero, and there were rather separate numerals for each of the tens (10, 20, 30, etc.).
The actual numeral system, including positional notation and use of zero, is in principle independent of the glyphs used, and significantly younger than the Brahmi numerals.
Development
The "Galley" method of division.
The place-value system is used in the Bakhshali Manuscript. Although date of the composition of the manuscript is uncertain, the language used in the manuscript indicates that it could not have been composed any later than 400 AD.[8] The development of the positional decimal system takes its origins in Indian mathematics during the Gupta period. Around 500 CE the astronomer Aryabhata uses the word kha ("emptiness") to mark "zero" in tabular arrangements of digits. The 7th century Brahmasphuta Siddhanta contains a comparatively advanced understanding of the mathematical role of zero. The Sanskrit translation of the lost 5th century Prakrit Jaina cosmological text Lokavibhaga may preserve an early instance of positional use of zero.[9]
These Indian developments were taken up in Islamic mathematics in the 8th century, as recorded in al-Qifti's Chronology of the scholars (early 13th century).[10]
The numeral system came to be known to both the Muslim/Persian mathematician Al-Khwarizmi, who wrote a book, On the Calculation with Hindu Numerals in about 825, and the Persian mathematician Al-Kindi, who wrote four volumes, On the Use of the Indian Numerals (كتاب في استعمال العداد الهندي [kitāb fī isti'māl al-'adād al-hindī]) around 830. These earlier text did not used the Hindu numerals. Kushyar ibn Labban who wrote Kitab fi usul hisab al-hind(Principles of Hindu Reckoning) is one of the oldest surviving manuscript used the Hindu numerals.[11] These books are principally responsible for the diffusion of the Indian system of numeration throughout the Islamic world and ultimately also to Europe [2]. The first dated and undisputed inscription showing the use of zero at is at Gwalior, dating to 876 AD.
In 10th century Islamic mathematics, the system was extended to include fractions, as recorded in a treatise by Syrian mathematician Abu'l-Hasan al-Uqlidisi in 952–953.[12]
Adoption in Europe
Main article: Arabic numeralsIn Christian Europe, the first mention and representation of Hindu-Arabic numerals (from one to nine, without zero), is in the Codex Vigilanus, an illuminated compilation of various historical documents from the Visigothic period in Spain, written in the year 976 by three monks of the Riojan monastery of San Martín de Albelda. Between 967 and 969, Gerbert of Aurillac discovered and studied Arab science in the Catalan abbeys. Later he obtained from these places the book De multiplicatione et divisione (On the multiplication and division). After having become pope Sylvester II in the year 999, he introduced a new model of abacus, the so called Abacus of Gerbert, by adopting tokens representing Hindu-Arab numerals, from one to nine.
Leonardo Fibonacci brought this system to Europe. His book Liber Abaci introduced Arabic numerals, the use of zero, and the decimal place system to the Latin world. The numeral system came to be called "Arabic" by the Europeans. It was used in European mathematics from the 12th century, and entered common use from the 15th century to replace Roman numerals. Robert Chester translated the Latin into English.[citation needed]
The familiar shape of the Western Arabic glyphs as now used with the Latin alphabet, (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) are the product of the late 15th to early 16th century, when they enter early typesetting. Muslim scientists used the Babylonian numeral system, and merchants used the Abjad numerals, a system similar to the Greek numeral system and the Hebrew numeral system. Similarly, Fibonacci's introduction of the system to Europe was restricted to learned circles. The credit of first establishing widespread understanding and usage of the decimal positional notation among the general population goes to Adam Ries, an author of the German Renaissance, whose 1522 Rechenung auff der linihen und federn was targeted at the apprentices of businessmen and craftsmen.
Adoption in East Asia
In China, Gautama Siddha introduced Indian numerals with zero in 718, but Chinese mathematicians did not find them useful, as they had already had the decimal positional counting rods.[13][14]
In Chinese numerals, a circle (〇) is used to write zero in Suzhou numerals. Many historians think it was imported from Indian numerals by Gautama Siddha in 718, but some think it was created from the Chinese text space filler "□".[13]
Chinese and Japanese finally adopted the Hindu–Arabic numerals in the 19th century, abandoning counting rods.
Spread of the Western Arabic variant
The "Western Arabic" numerals as they were in common use in Europe since the Baroque period have secondarily found worldwide use together with the Latin alphabet, and even significantly beyond the contemporary spread of the Latin alphabet, intruding into the writing systems in regions where other variants of the Hindu–Arabic numerals had been in use, but also in conjunction with Chinese and Japanese writing (see Chinese numerals, Japanese numerals).
See also
Notes
- ^ David Eugene Smith and Louis Charles Karpinski, The Hindu–Arabic Numerals, 1911
- ^ Collier's encyclopedia, with bibliography and index William Darrach Halsey, Emanuel Friedman - 1983. "When the Arabian empire was expanding and contact was made with India, the Hindu numeral system and the early algorithms were adopted by the Arabs"
- ^ Essays on ancient India By Raj Kumar - Discovery Publishing House, 2003.
- ^ Geometry By Roger Fenn, Springer, 2001
- ^ The Unicode Standard 5.0 – Electronic edition, Chapter 8 Middle Eastern Scripts
- ^ Language may shape human thought, NewScientist.com news service, Celeste Biever, 19:00 19 August 2004.
- ^ Flegg (2002), p. 6ff.
- ^ Pearce, Ian (May 2002). "The Bakhshali manuscript". The MacTutor History of Mathematics archive. http://www-history.mcs.st-andrews.ac.uk/HistTopics/Bakhshali_manuscript.html. Retrieved 2007-07-24.
- ^ Ifrah, G. The Universal History of Numbers: From prehistory to the invention of the computer. John Wiley and Sons Inc., 2000. Translated from the French by David Bellos, E.F. Harding, Sophie Wood and Ian Monk
- ^ al-Qifti's account does not pertain to the numerals explicitly, but to the reception of Indian astronomy[1]:
- ... a person from India presented himself before the Caliph al-Mansur in the year 776 who was well versed in the siddhanta method of calculation related to the movement of the heavenly bodies, and having ways of calculating equations based on the half-chord [essentially the sine] calculated in half-degrees ... Al-Mansur ordered this book to be translated into Arabic, and a work to be written, based on the translation, to give the Arabs a solid base for calculating the movements of the planets ... The book presented by the Indian scholar was probably the Brahmasphuta Siddhanta itself.
- ^ Martin Levey and Marvin Petruck, Principles of Hindu Reckonging, translation of Kushyar ibn Labban Kitab fi usul hisab al-hind, p3, University of Wisconsin Press, 1965
- ^ Berggren, J. Lennart (2007). "Mathematics in Medieval Islam". The Mathematics of Egypt, Mesopotamia, China, India, and Islam: A Sourcebook. Princeton University Press. p. 518. ISBN 9780691114859.
- ^ a b Qian, Baocong (1964), Zhongguo Shuxue Shi (The history of Chinese mathematics), Beijing: Kexue Chubanshe
- ^ Wáng, Qīngxiáng (1999), Sangi o koeta otoko (The man who exceeded counting rods), Tokyo: Tōyō Shoten, ISBN 4-88595-226-3
References
- Flegg, Graham (2002). Numbers: Their History and Meaning. Courier Dover Publications. ISBN 0-486-42165-1.
- The Arabic numeral system
Bibliography
- Menninger, Karl W. (1969). Number Words and Number Symbols: A Cultural History of Numbers. MIT Press. ISBN 0-262-13040-8.
Categories:- Numeration
- Numerals
- Elementary mathematics
Wikimedia Foundation. 2010.