Centrifugal force (rotating reference frame)

This article is about the fictitious force related to rotating reference frames. For other uses, see Centrifugal force.

Classical mechanics
$\mathbf{F} = m \mathbf{a}$ Newton's Second Law
History of classical mechanics · Timeline of classical mechanics
Branches Statics · Dynamics / Kinetics · Kinematics · Applied mechanics · Celestial mechanics · Continuum mechanics · Statistical mechanics
Formulations Newtonian mechanics (Vectorial mechanics) Analytical mechanics: Lagrangian mechanics Hamiltonian mechanics
Fundamental concepts Space · Time · Velocity · Speed · Mass · Acceleration · Gravity · Force · Impulse · Torque / Moment / Couple · Momentum · Angular momentum · Inertia · Moment of inertia · Reference frame · Energy · Kinetic energy · Potential energy · Mechanical work · Virtual work · D'Alembert's principle
Core topics Rigid body · Rigid body dynamics · Euler's equations (rigid body dynamics) · Motion · Newton's laws of motion · Newton's law of universal gravitation · Equations of motion · Inertial frame of reference · Non-inertial reference frame · Rotating reference frame · Fictitious force · Linear motion · Mechanics of planar particle motion · Displacement (vector) · Relative velocity · Friction · Simple harmonic motion · Harmonic oscillator · Vibration · Damping · Damping ratio · Rotational motion · Circular motion · Uniform circular motion · Non-uniform circular motion · Centripetal force · Centrifugal force · Centrifugal force (rotating reference frame) · Reactive centrifugal force · Coriolis force · Pendulum · Rotational speed · Angular acceleration · Angular velocity · Angular frequency · Angular displacement
Scientists Galileo Galilei · Isaac Newton · Jeremiah Horrocks · Leonhard Euler · Jean le Rond d'Alembert · Alexis Clairaut · Joseph Louis Lagrange · Pierre-Simon Laplace · William Rowan Hamilton · Siméon-Denis Poisson
v · d · e

Centrifugal force (from Latin centrum "center" and fugere "to flee") can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame. Because a rotating frame is an example of a non-inertial reference frame, Newton's laws of motion do not accurately describe the dynamics within the rotating frame. However, a rotating frame can be treated as if it were an inertial frame so that Newton's laws can be used if so-called fictitious forces (also known as inertial or pseudo- forces) are included in the sum of external forces on an object. The centrifugal force is what is usually thought of as the cause for apparent outward movement like that of passengers in a vehicle turning a corner, of the weights in a centrifugal governor, and of particles in a centrifuge. From the standpoint of an observer in an inertial frame, the effects can be explained as results of inertia without invoking the centrifugal force. Centrifugal force should not be confused with centripetal force or the reactive centrifugal force, both of which are real forces independent of the frame of the observer.

Analysis of motion within rotating frames can be greatly simplified by the use of the fictitious forces. By starting with an inertial frame, where Newton's laws of motion hold, and keeping track of how the time derivatives of a position vector change when transforming to a rotating reference frame, the various fictitious forces and their forms can be identified. Rotating frames and fictitious forces can often reduce the description of motion in two dimensions to a simpler description in one dimension (corresponding to a co-rotating frame). In this approach, circular motion in an inertial frame, which only requires the presence of a centripetal force, becomes the balance between the real centripetal force and the frame-determined centrifugal force in the rotating frame where the object appears stationary. If a rotating frame is chosen so that just the angular position of an object is held fixed, more complicated motion, such as elliptical and open orbits, appears because the centripetal and centrifugal forces will not balance. The general approach however is not limited to these co-rotating frames, but can be equally applied to objects at motion in any rotating frame.

In classical Newtonian physics

Although Newton's laws of motion hold exclusively in inertial frames, often times is far more convenient and more advantageous to describe the motion of objects within a rotating reference frame.^[1][2] Sometimes the calculations are simpler (an example is inertial circles), and sometimes the intuitive picture coincides more closely with the rotational frame (an example is sedimentation in a centrifuge). By treating the extra acceleration terms due to the rotation of the frame as if they were forces, subtracting them from the physical forces, it's possible to treat the second time derivative of position (relative to the rotating frame) as absolute acceleration. Thus the analysis using Newton's laws of motion can proceed as if the reference frame was inertial, provided the fictitious force terms are included in the sum of external forces.^[3] For example, centrifugal force is used in the FAA pilot's manual in describing turns.^[4] Other examples are such systems as planets, centrifuges, carousels, turning cars, spinning buckets, and rotating space stations.^[5][6][7]

A disadvantage of a rotating reference frame is that it can be more difficult to apply special relativity (for example, from the perspective of the Earth the stars seem to traverse many light-years each day). It is possible to do so if a metric tensor is introduced, but the speed of light may not be constant and clocks within the frame are not synchronized.^[8][9]

There are three general scenarios in which this concept of a fictitious centrifugal force arises when describing motion:^[10]

1. When the motion is described relative to a rotating reference frame about a fixed axis at the origin of the coordinate system. For observations made in the rotating frame, all objects appear to be under the influence of a radially outward force that is proportional to the distance from the axis of rotation and to the square of the rate of rotation (angular velocity) of the frame.
2. When the motion is described using an accelerated local reference frame attached to a moving body, for example, the frame of passengers in a car as it rounds a corner.^[10] In this case, rotation is again involved, this time about the center of curvature of the path of the moving body. The first context can be seen as a special scenario within this second context in which the origin of the coordinate system and the axis of rotation are always coincident. In both, the centrifugal force is zero when the rate of rotation of the reference frame is zero, independent of the motions of objects in the frame.^[11]
3. The third context is the most general, and subsumes the first two, as well as stationary curved coordinates (e.g., polar coordinates).^{[1][12][13][14]} The centrifugal force appears when the terms for the radial component of the equation of motion are rearranged to resemble Newton's second law for one-dimensional motion. Therefore, the centrifugal force is simply the sign-reversal of the centripetal acceleration for motion along curves where the radial distance is fixed and is related to the Christoffel symbol term related to that curvature. While no rotation is necessary in this derivation, reapplying Newtonian definitions of force and acceleration to the rearranged equation necessarily implies observing the motion from a co-rotating frame of reference.^[15][16]

In each of these scenarios, the centrifugal force is an inertial force used for convenience and implied by a specific, non-inertial reference frame.

If objects are seen as moving within a rotating frame, this movement results in another fictitious force, the Coriolis force; and if the rate of rotation of the frame is changing, a third fictitious force, the Euler force is experienced.^[17] Together, these three fictitious forces allow for the creation of correct equations of motion in a rotating reference frame.^[11]

Derivation

Main article: Rotating reference frame

See also: Fictitious force and Mechanics of planar particle motion

For the following formalism, the rotating frame of reference is regarded as a special case of a non-inertial reference frame that is rotating relative to an inertial reference frame denoted the stationary frame.

Velocity

In a rotating frame of reference, the time derivatives of the position vector r, such as velocity and acceleration vectors, of an object will differ from the time derivatives in the stationary frame according to the frame's rotation. The first time derivative [dr/dt] evaluated within a reference frame with a coincident origin at r = 0 but rotating with the absolute angular velocity ω is:^[18]

$\frac{\operatorname{d}\boldsymbol{r}}{\operatorname{d}t} = \left[\frac{\operatorname{d}\boldsymbol{r}}{\operatorname{d}t}\right] + \boldsymbol{\omega} \times \boldsymbol{r}\ ,$

where $\times$ denotes the vector cross product and square brackets [...] denote evaluation in the rotating frame of reference. In other words, the apparent velocity in the rotating frame is altered by the amount of the apparent rotation $\boldsymbol{\omega} \times \boldsymbol{r}$ at each point, which is perpendicular to both the vector from the origin r and the axis of rotation ω and directly proportional in magnitude to each of them. The vector ω has magnitude ω equal to the rate of rotation and is directed along the axis of rotation according to the right-hand rule.

Acceleration

Newton's law of motion for a particle of mass m written in vector form is:

$\boldsymbol{F} = m\boldsymbol{a}\ ,$

where F is the vector sum of the physical forces applied to the particle and a is the absolute acceleration (that is, acceleration in a stationary frame) of the particle, given by:

$\boldsymbol{a}=\frac{\operatorname{d}^2\boldsymbol{r}}{\operatorname{d}t^2} \ ,$

where r is the position vector of the particle.

By twice applying the transformation above from the stationary to the rotating frame, the absolute acceleration of the particle can be written as:

$\begin{align} \boldsymbol{a} &=\frac{\operatorname{d}^2\boldsymbol{r}}{\operatorname{d}t^2} = \frac{\operatorname{d}}{\operatorname{d}t}\frac{\operatorname{d}\boldsymbol{r}}{\operatorname{d}t} = \frac{\operatorname{d}}{\operatorname{d}t} \left( \left[\frac{\operatorname{d}\boldsymbol{r}}{\operatorname{d}t}\right] + \boldsymbol{\omega} \times \boldsymbol{r}\ \right) \\ &= \left[ \frac{\operatorname{d}^2 \boldsymbol{r}}{\operatorname{d}t^2} \right] + \frac{\operatorname{d} \boldsymbol{\omega}}{\operatorname{d}t}\times\boldsymbol{r} + 2 \boldsymbol{\omega}\times \left[ \frac{\operatorname{d} \boldsymbol{r}}{\operatorname{d}t} \right] + \boldsymbol{\omega}\times ( \boldsymbol{\omega} \times \boldsymbol{r}) \ . \end{align}$

Force

The apparent acceleration in the rotating frame is [d²r/dt²]. An observer unaware of the rotation would expect this to be zero in the absence of outside forces. However Newton's laws of motion apply only in the stationary frame and describe dynamics in terms of the absolute acceleration d²r/dt². Therefore the observer perceives the extra terms as contributions due to fictitious forces. These terms in the apparent acceleration are independent of mass; so it appears that each of these fictitious forces, like gravity, pulls on an object in proportion to its mass. When these forces are added, the equation of motion has the form:^[19][20][21]

$\boldsymbol{F} - m\frac{\operatorname{d} \boldsymbol{\omega}}{\operatorname{d}t}\times\boldsymbol{r} - 2m \boldsymbol{\omega}\times \left[ \frac{\operatorname{d} \mathbf{r}}{\operatorname{d}t} \right] - m\boldsymbol{\omega}\times (\boldsymbol{\omega}\times \boldsymbol{r})$ $= m\left[ \frac{\operatorname{d}^2 \boldsymbol{r}}{\operatorname{d}t^2} \right] \ .$

From the perspective of the rotating frame, the additional force terms are experienced just like the real external forces and contribute to the apparent acceleration.^[22][23] The additional terms on the force side of the equation can be recognized as, reading from left to right, the Euler force $m \operatorname{d}\boldsymbol{\omega}/\operatorname{d}t \times\boldsymbol{r}$, the Coriolis force $2m \boldsymbol{\omega}\times \left[ \operatorname{d} \boldsymbol{r}/\operatorname{d}t \right]$, and the centrifugal force $m\boldsymbol{\omega}\times (\boldsymbol{\omega}\times \boldsymbol{r})$, respectively.^[24] Unlike the other two fictitious forces, the centrifugal force always points radially outward from the axis of rotation of the rotating frame, with magnitude mω²r, and unlike the Coriolis force in particular, it is independent of the motion of the particle in the rotating frame. As expected, for a non-rotating inertial frame of reference $(\boldsymbol\omega=0)$ the centrifugal force and all other fictitious forces disappear.^[25]

Absolute rotation

Main article: Absolute rotation

Three scenarios were suggested by Newton to answer the question of whether the absolute rotation of a local frame can be detected; that is, if an observer can decide whether an observed object is rotating or if the observer is rotating.^[26][27]

• The shape of the surface of water rotating in a bucket. Centrifugal force will force the surface of the water to be concave.
• The tension in a string joining two spheres rotating about their center of mass. The tension in the string will be proportional to the centrifugal force on each sphere as it rotates around the common center of mass.
• The oblateness of a sphere of freely flowing material. The oblate spheroid shape reflects, following Clairaut's theorem, the balance between containment by gravitational attraction and dispersal by centrifugal force.

In these scenarios, the effects attributed to centrifugal force are only observed in the local frame (the frame in which the object is stationary) if the object is undergoing absolute rotation relative to an inertial frame. By contrast, in an inertial frame, the observed effects arise as a consequence of the inertia and the known forces without the need to introduce a centrifugal force.

Examples

Below several examples illustrate both the stationary and rotating frames of reference, and the role of centrifugal force and its relation to Coriolis force in rotating frameworks. For more examples see Fictitious force, rotating bucket and rotating spheres.

Dropping ball

A ball moving vertically along the axis of rotation in a stationary frame appears to spiral downward in the rotating frame. The right panel shows a downward view in the rotating frame. The rate of rotation |ω| = ω is assumed constant in time

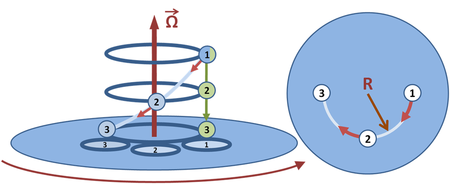
An example of straight-line motion as seen in a stationary frame is a ball that steadily drops at a constant rate parallel to the axis of rotation. From a stationary frame of reference it moves in a straight line, but from the rotating frame it moves in a spiral. The projection of the spiral motion in a rotating horizontal plane is shown at the right of the figure. Because the projected horizontal motion in the rotating frame is a circular motion, the ball's motion requires an inward centripetal force, provided in this case by a fictitious force that produces the apparent spiral motion. This force is the sum of an outward centrifugal force and an inward Coriolis force. The Coriolis force overcompensates the centrifugal force by exactly the required amount to provide the necessary centripetal force to achieve circular motion.

Banked turn

Main article: Banked turn

See also: Centripetal force#Example: The banked turn and Reactive centrifugal force#Example: The turning car

Riding a car around a curve, we take a personal view that we are at rest in the car, and should be undisturbed in our seats. Nonetheless, we feel sideways force applied to us from the seats and doors and a need to lean to one side. To explain the situation, we propose a centrifugal force that is acting upon us and must be combated. Interestingly, we find this discomfort is reduced when the curve is banked, tipping the car inward toward the center of the curve.

A different point of view is that of the highway designer. The designer views the car as executing curved motion and therefore requiring an inward centripetal force to impel the car around the turn. By banking the curve, the force exerted upon the car in a direction normal to the road surface has a horizontal component that provides this centripetal force. That means the car tires no longer need to apply a sideways force to the car, but only a force perpendicular to the road. By choosing the angle of bank to match the car's speed around the curve, the car seat transmits only a perpendicular force to the passengers, and the passengers no longer feel a need to lean nor feel a sideways push by the car seats or doors.^[28]

Earth

A calculation for Earth at the equator (ω = 2π / 86164 seconds, r = 6378100 meters) shows that an object experiences a centrifugal force equal to approximately 1/289 of standard gravity.^[29] Because centrifugal force increases according to the square of ω, one would expect gravity to be cancelled for an object travelling 17 times faster than the Earth's rotation, and in fact satellites in low orbit at the equator complete 17 full orbits in one day.^[30]

Gravity diminishes according to the inverse square of distance, but centrifugal force increases in direct proportion to the distance. Thus a circular geosynchronous orbit has a radius of 42164 km; 42164/6378.1 = 6.61, the cube root of 289.

Planetary motion

See also: Orbit and Kepler's laws of planetary motion

Centrifugal force arises in the analysis of orbital motion and, more generally, of motion in a central-force field: in the case of a two-body problem, it is easy to convert to an equivalent one-body problem with force directed to or from an origin, and motion in a plane,^[31] so we consider only that.

The symmetry of a central force lends itself to a description in polar coordinates. The dynamics of a mass, m, expressed using Newton's second law of motion (F = ma), becomes in polar coordinates:^[32][33]

$\boldsymbol{F} = m((\ddot r - r \dot \theta^2) \boldsymbol{\hat r} + (r \ddot\theta + 2 \dot r \dot\theta) \boldsymbol{\hat \theta})$

where $\boldsymbol{F}$ is the force accelerating the object and the "hat" variables are unit direction vectors ($\boldsymbol{\hat r}$ points in the centrifugal or outward direction, and $\boldsymbol{\hat \theta}$ is orthogonal to it).

In the case of a central force, relative to the origin of the polar coordinate system, $\boldsymbol{F}$ can be replaced by $F(r) \boldsymbol{\hat r}$, meaning the entire force is the component in the radial direction. An inward force of gravity would therefore correspond to a negative-valued F(r).

The components of F = ma along the radial direction therefore reduce to

$F(r) = m(\ddot r - r \dot\theta^2)$

in which the term proportional to the square of the rate of rotation appears on the acceleration side as a "centripetal acceleration", that is, a negative acceleration term in the $\boldsymbol{\hat r}$ direction.^[34] In the special case of a planet in circular orbit around its star, for example, where $\ddot r$ is zero, the centripetal acceleration alone is the entire acceleration of the planet, curving its path toward the sun under the force of gravity, the negative F(r).

As pointed out by Taylor,^[35] for example, it is sometimes convenient to work in a co-rotating frame, that is, one rotating with the object so that the angular rate of the frame, ω, equals the $\dot\theta$ of the object in the stationary frame. In such a frame, the observed $\dot \theta$ is zero and $\ddot r$ alone is treated as the acceleration: so in the equation of motion, the $m r \dot\theta^2$ term is "reincarnated on the force side of the equation (with opposite signs, of course) as the centrifugal force mω²r in the radial equation":^[35] The "reincarnation" on the force side of the equation is necessary because, without this force term, observers in the rotating frame would find they could not predict the motion correctly. They would have an incorrect radial equation:

$F(r) + m r \dot\theta^2 = m\ddot r$

where the $m r \dot\theta^2$ term is known as the centrifugal force. The centrifugal force term in this equation is called a "fictitious force", "apparent force", or "pseudo force", as its value varies with the rate of rotation of the frame of reference. When the centrifugal force term is expressed in terms of parameters of the rotating frame, replacing $\dot\theta$ with ω, it can be seen that it is the same centrifugal force previously derived for rotating reference frames.

Because of the absence of a net force in the azimuthal direction, conservation of angular momentum allows the radial component of this equation to be expressed solely with respect to the radial coordinate, r, and the angular momentum $L=m \dot\theta r^2$, yielding the radial equation (a "fictitious one-dimensional problem"^[31] with only an r dimension):

$F(r) + \frac{L^2}{mr^3} = m \ddot r$.

The L² / mr³ term is again the centrifugal force, a force component induced by the rotating frame of reference. The equations of motion for r that result from this equation for the rotating 2D frame are the same that would arise from a particle in a fictitious one-dimensional scenario under the influence of the force in the equation above.^[31] If F(r) represents gravity, it is a negative term proportional to 1/r², so the net acceleration in r in the rotating frame depends on a difference of reciprocal square and reciprocal cube terms, which are in balance in a circular orbit but otherwise typically not. This equation of motion is similar to one originally proposed by Leibniz.^[36] Given r, the rate of rotation is easy to infer from the constant angular momentum L, so a 2D solution can be easily reconstructed from a 1D solution of this equation.

When the angular velocity of this co-rotating frame is not constant, that is, for non-circular orbits, other fictitious forces—the Coriolis force and the Euler force—will arise, but can be ignored since they will cancel each other, yielding a net zero acceleration transverse to the moving radial vector, as required by the starting assumption that the $\hat r$ vector co-rotates with the planet.^[37] In the special case of circular orbits, in order for the radial distance to remain constant the outward centrifugal force must cancel the inward force of gravity; for other orbit shapes, these forces will not cancel, so r will not be constant.

History

Main article: History of centrifugal and centripetal forces

Concepts of centripetal and centrifugal force played a key early role in establishing the set of inertial frames of reference and the significance of fictitious forces, even aiding in the development of general relativity in which gravity itself becomes a fictitious force.^[38]

Applications

The operations of numerous common rotating mechanical systems are most easily conceptualized in terms of centrifugal force. For example:

• A centrifugal governor regulates the speed of an engine by using spinning masses that move radially, adjusting the throttle, as the engine changes speed. In the reference frame of the spinning masses, centrifugal force causes the radial movement.
• A centrifugal clutch is used in small engine-powered devices such as chain saws, go-karts and model helicopters. It allows the engine to start and idle without driving the device but automatically and smoothly engages the drive as the engine speed rises. Inertial drum brake ascenders used in rock climbing and the inertia reels used in many automobile seat belts operate on the same principle.
• Centrifugal forces can be used to generate artificial gravity, as in proposed designs for rotating space stations. The Mars Gravity Biosatellite will study the effects of Mars-level gravity on mice with gravity simulated in this way.
• Spin casting and centrifugal casting are production methods that uses centrifugal force to disperse liquid metal or plastic throughout the negative space of a mold.
• Centrifuges are used in science and industry to separate substances. In the reference frame spinning with the centrifuge, the centrifugal force induces a hydrostatic pressure gradient in fluid-filled tubes oriented perpendicular to the axis of rotation, giving rise to large buoyant forces which push low-density particles inward. Elements or particles denser than the fluid move outward under the influence of the centrifugal force. This is effectively Archimedes' principle as generated by centrifugal force as opposed to being generated by gravity.
• Some amusement rides make use of centrifugal forces. For instance, a Gravitron's spin forces riders against a wall and allows riders to be elevated above the machine's floor in defiance of Earth's gravity.

Nevertheless, all of these systems can also be described without requiring the concept of centrifugal force, in terms of motions and forces in a stationary frame, at the cost of taking somewhat more care in the consideration of forces and motions within the system.

See also

Physics portal

• Equivalence principle
• Folk physics
• Lamm equation
• Lagrangian point

Footnotes

1. ^ ^{a b} Stephen T. Thornton & Jerry B. Marion (2004). Classical Dynamics of Particles and Systems (5th ed.). Belmont CA: Brook/Cole. Chapter 10. ISBN 0534408966. http://worldcat.org/oclc/52806908&referer=brief_results. 
2. ^ John Robert Taylor (2004). Classical Mechanics. Sausalito CA: University Science Books. Chapter 9, pp. 327 ff. ISBN 189138922X. http://books.google.com/?id=P1kCtNr-pJsC&pg=PP1&dq=isbn=189138922X. 
3. ^ Robert Resnick & David Halliday (1966). Physics. Wiley. p. 121. ISBN 0471345245. http://books.google.com/books?lr=&as_brr=0&q=%22cannot+associate+them+with+any+particular+body+in+the+environment+of+the+particle%22+inauthor%3ADavid+inauthor%3AHalliday&btnG=Search+Books. 
4. ^ Federal Aviation Administration (2007). Pilot's Encyclopedia of Aeronautical Knowledge. Oklahoma City OK: Skyhorse Publishing Inc.. Figure 3–21. ISBN 1602390347. http://books.google.com/?id=m5V04SXE4zQC&pg=PT33&lpg=PT33&dq=+%22angle+of+bank%22. 
5. ^ Richard Hubbard (2000). Boater's Bowditch: The Small Craft American Practical Navigator. NY: McGraw-Hill Professional. p. 54. ISBN 0071361367. http://books.google.com/?id=nfWSxRr8VP4C&pg=PA54&dq=tides+centrifugal. 
6. ^ Lawrence K. Wang & Norman C. Pereira (1979). Handbook of Environmental Engineering: Air and Noise Pollution Control. Humana Press. p. 63. ISBN 0896030016. http://books.google.com/?id=FkSnJZSbmxUC&pg=PA63&dq=cyclone+centrifugal. 
7. ^ Lee M. Grenci & Jon M. Nese (2001). A World of Weather: Fundamentals of Meteorology. Kendall Hunt. p. 272. ISBN 0787277169. http://books.google.com/?id=oh8lqM5obuYC&pg=PA272&dq=meteorology+centrifugal. 
8. ^ Philip Gibbs. "Physics FAQ". University of California Riverside. http://math.ucr.edu/home/baez/physics/Relativity/SR/acceleration.html. 
9. ^ T.A.Weber. "Measurements on a rotating frame in relativity, and the Wilson and Wilson experiment". pp. 946–953. http://www.physics.princeton.edu/~mcdonald/examples/EM/weber_ajp_65_946_97.pdf. 
10. ^ ^{a b} See p. 5 in Donato Bini, Paolo Carini, Robert T Jantzen (1997). "The intrinsic derivative and centrifugal forces in general relativity: I. Theoretical foundations". International Journal of Modern Physics D 6 (1). http://www34.homepage.villanova.edu/robert.jantzen/research/articles/idcf1.pdf. . The companion paper is Donato Bini, Paolo Carini, Robert T Jantzen (1997). "The intrinsic derivative and centrifugal forces in general relativity: II. Applications to circular orbits in some stationary axisymmetric spacetimes". International Journal of Modern Physics D 6 (1). http://www34.homepage.villanova.edu/robert.jantzen/research/articles/idcf2.pdf. 
11. ^ ^{a b} Alexander L. Fetter & John Dirk Walecka (2003). Theoretical Mechanics of Particles and Continua. Courier Dover Publications. pp. 38–39.. ISBN 0486432610. http://books.google.com/books?id=olMpStYOlnoC&pg=PA39. 
12. ^ Francis B. Hildebrand (1992). Methods of Applied Mathematics. Dover. p. 156. 
13. ^ Donald Allan McQuarrie (2000). Statistical Mechanics. University Science Books. 
14. ^ Hans-Jurgen Weber & George Brown Arfken (2004). Essential Mathematical Methods for Physicists. Academic Press. p. 843. 
15. ^ Atam Parkash Arya (1990). Introduction to Classical Mechanics. Allyn and Bacon. p. 231. ISBN 0205120288. 
16. ^ Jeremy B. Tatum "Celestial Mechanics" Chapter 16
17. ^ Jerrold E. Marsden & Tudor S. Ratiu (1999). Introduction to Mechanics and Symmetry: A Basic Exposition of Classical Mechanical Systems. Springer. p. 251. ISBN 038798643X. http://books.google.com/?id=I2gH9ZIs-3AC&pg=PA251&vq=Euler+force&dq=isbn=038798643X. 
18. ^ John L. Synge (2007). Principles of Mechanics (Reprint of Second Edition of 1942 ed.). Read Books. p. 347. ISBN 1406746703. http://books.google.com/?id=YZjIg4Mo56UC&pg=PA347&dq=rotating+fictitious+force. 
19. ^ Taylor (2005). p. 342.
20. ^ LD Landau and LM Lifshitz (1976). Mechanics (Third ed.). Oxford: Butterworth-Heinemann. p. 128. ISBN 978-0-7506-2896-9. http://books.google.com/?id=e-xASAehg1sC&pg=PA40&dq=isbn=9780750628969. 
21. ^ Louis N. Hand, Janet D. Finch (1998). Analytical Mechanics. Cambridge University Press. p. 267. ISBN 0521575729. http://books.google.com/?id=1J2hzvX2Xh8C&pg=PA267&vq=fictitious+forces&dq=Hand+inauthor:Finch. 
22. ^ Mark P Silverman (2002). A universe of atoms, an atom in the universe (2 ed.). Springer. p. 249. ISBN 0387954376. http://books.google.com/?id=-Er5pIsYe_AC&pg=PA249. 
23. ^ Taylor (2005). p. 329.
24. ^ Cornelius Lanczos (1986). The Variational Principles of Mechanics (Reprint of Fourth Edition of 1970 ed.). Dover Publications. Chapter 4, §5. ISBN 0-486-65067-7. http://books.google.com/books?id=ZWoYYr8wk2IC&pg=PA103. 
25. ^ Morton Tavel (2002). Contemporary Physics and the Limits of Knowledge. Rutgers University Press. p. 93. ISBN 0813530776. http://books.google.com/?id=SELS0HbIhjYC&pg=PA95&dq=Einstein+equivalence+laws+physics+frame. "Noninertial forces, like centrifugal and Coriolis forces, can be eliminated by jumping into a reference frame that moves with constant velocity, the frame that Newton called inertial." 
26. ^ Louis N. Hand, Janet D. Finch (1998). Analytical Mechanics. Cambridge University Press. p. 324. ISBN 0521575729. http://books.google.com/?id=1J2hzvX2Xh8C&pg=PA324. 
27. ^ I. Bernard Cohen, George Edwin Smith (2002). The Cambridge companion to Newton. Cambridge University Press. p. 43. ISBN 0521656966. http://books.google.com/?id=3wIzvqzfUXkC&pg=PA43. 
28. ^ Lawrence S. Lerner (1996). Physics for Scientists and Engineers. Jones & Bartlett Publishers. p. 129. ISBN 0763702536. http://books.google.com/?id=Bsruo5nz1eIC&pg=PA129. 
29. ^ Bowser, Edward Albert (1920). An elementary treatise on analytic mechanics: with numerous examples. D. Van Nostrand Company. http://books.google.com/?id=mE4GAQAAIAAJ&pg=PA358&lpg=PA358. 
30. ^ Robert and Gary Ehrlich (1998). What if you could unscramble an egg?. Rutgers University Press. ISBN 9780813525488. http://books.google.com/?id=DhYL6A0Dvw4C&pg=PA120&lpg=PA120. 
31. ^ ^{a b c} Herbert Goldstein (1950). Classical Mechanics. Addison-Wesley. pp. 24–25, 61–64. ISBN 0201029189. http://books.google.com/?id=A_RQAAAAMAAJ&q=%22fictitious+one-dimensional+problem%22+intitle:mechanics+inauthor:goldstein&dq=%22fictitious+one-dimensional+problem%22+intitle:mechanics+inauthor:goldstein. 
32. ^ John Clayton Taylor (2001). Hidden unity in nature's laws. Cambridge University Press. p. 26. ISBN 0521659388. http://books.google.com/?id=VEn8Orko4FgC&pg=PA26. 
33. ^ Henry M. Stommel and Dennis W. Moore (1989). An introduction to the Coriolis force. Columbia University Press. pp. 28–40. ISBN 9780231066365. http://books.google.com/?id=-JQx_t3yGB4C&pg=PA36&dq=centrifugal+inauthor:stommel+inauthor:moore. 
34. ^ Taylor (2005). p. 358-9.
35. ^ ^{a b} Taylor (2005). p. 359.
36. ^ Frank Swetz, John Fauvel, Otto Bekken, Bengt Johansson, and Victor Katz (1997). Learn from the masters!. Mathematical Association of America. pp. 268–269. ISBN 9780883857038. http://books.google.com/?id=gqGLoh-WYrEC&pg=PA269&dq=reaction+fictitious+rotating+frame+%22centrifugal+force%22. 
37. ^ Whiting, J.S.S. (November 1983). "Motion in a central-force field". Physics Education 18 (6): pp. 256–257. Bibcode 1983PhyEd..18..256W. doi:10.1088/0031-9120/18/6/102. ISSN 0031-9120. http://www.iop.org/EJ/article/0031-9120/18/6/102/pev18i6p256.pdf. Retrieved May 7, 2009. 
38. ^ Hans Christian Von Baeyer (2001). The Fermi Solution: Essays on science (Reprint of 1993 ed.). Courier Dover Publications. p. 78. ISBN 0486417077. http://books.google.com/?id=VhJr9Qx8ohsC&pg=PA78&dq=gravity+like+%22centrifugal+force%22. 

References

• John Robert Taylor (2005). Classical Mechanics. University Science Books. ISBN 189138922X. http://books.google.com/?id=P1kCtNr-pJsC&pg=PP1&dq=isbn=189138922X. 

External links

• Centripetal force and Centrifugal force, from an online Regents Exam physics tutorial by the Oswego City School District
• Centrifugal force at the HyperPhysics concepts site
• Centripetal and Centrifugal Forces at MathPages
• Motion over a flat surface and a parabolic surface Java physlets by Brian Fiedler (from School of Meteorology at the University of Oklahoma) illustrating fictitious forces.
• Animation clip showing scenes as viewed from both a stationary and a rotating frame of reference, visualizing the Coriolis and centrifugal forces.
• John Baez: Does centrifugal force hold the Moon up?