Clairaut's theorem

For the interpretation of this theorem in terms of symmetry of second derivatives of a mapping $f \colon \mathbb{R}^n \to \mathbb{R}$, see Symmetry of second derivatives.

Figure 1: An ellipsoid

Figure 2: Wireframe rendering of an ellipsoid (oblate spheroid)

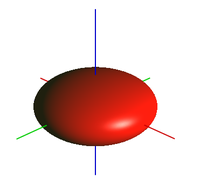
Clairaut's theorem, published in 1743 by Alexis Claude Clairaut in his Théorie de la figure de la terre, tirée des principes de l'hydrostatique,^[1] synthesized physical and geodetic evidence that the Earth is an oblate rotational ellipsoid.^[2][3] It is a general mathematical law applying to spheroids of revolution. It was initially used to relate the gravity at any point on the Earth's surface to the position of that point, allowing the ellipticity of the Earth to be calculated from measurements of gravity at different latitudes.

Formula

Clairaut's formula for the acceleration of gravity g on the surface of a spheroid at latitude φ, was:^[4][5]

$g = G \left[ 1 + \left(\frac{5}{2} m - f\right) \sin^2 \phi \right] \ ,$

where G is the value of the acceleration of gravity at the equator, m the ratio of the centrifugal force to gravity at the equator, and f the flattening of a meridian section of the earth, defined as:

$f = \frac {a-b}{a} \ ,$

(where a = semimajor axis, b=semiminor axis ).

Clairaut derived the formula under the assumption that the body was composed of concentric coaxial spheroidal layers of constant density.^[6] This work was subsequently pursued by Laplace, who relaxed the initial assumption that surfaces of equal density were spheroids.^[7] Stokes showed in 1849 that the theorem applied to any law of density so long as the external surface is a spheroid of equilibrium.^[8][9] A history of the subject, and more detailed equations for g can be found in Khan.^[10]

The above expression for g has been supplanted by the Somigliana equation:

$g = G \left[ \frac{1+k\sin^2 \phi}{\sqrt{1-e^2 \sin^2 \phi }} \right] \ ,$

where, for the Earth, G =9.7803267714 ms⁻²; k =0.00193185138639 ; e² =0.00669437999013.^[11]

Clairaut's relation

Main article: Clairaut's relation

A formal mathematical statement of Clairaut's theorem is:^[12]

Let γ be a geodesic on a surface of revolution S, let ρ be the distance of a point of S from the axis of rotation, and let ψ be the angle between γ and the meridians of S. Then ρ sin ψ is constant along γ. Conversely, if ρ sin ψ is constant along some curve γ in the surface, and if no part of γ is part of some parallel of S, then γ is a geodesic.

— Andrew Pressley: Elementary Differential Geometry, p. 183

Pressley (p. 185) explains this theorem as an expression of conservation of angular momentum about the axis of revolution when a particle slides along a geodesic under no forces other than those that keep it on the surface.

Geodesy

The spheroidal shape of the Earth is the result of the interplay between gravity and centrifugal force caused by the Earth's rotation about its axis.^[13][14] In his Principia, Newton proposed the equilibrium shape of a homogeneous rotating Earth was a rotational ellipsoid with a flattening f given by 1/230.^[15][16] As a result gravity increases from the equator to the poles. By applying Clairaut's theorem, Laplace was able to deduce from 15 gravity values that f = 1/330. A modern estimate is 1/298.25642.^[17] See Figure of the Earth for more detail.

For a detailed account of the construction of the reference Earth model of geodesy, see Chatfield.^[18]

Notes

1. ^ From the catalogue of the scientific books in the library of the Royal Society.
2. ^ Wolfgang Torge (2001). Geodesy: An Introduction (3rd ed.). Walter de Gruyter. p. 10. ISBN 3110170728. http://books.google.com/books?id=pFO6VB_czRYC&pg=PA109&dq=%22Clairaut%27s+theorem%22&lr=&as_brr=0&sig=ACfU3U34GaPhl4tA9duUMLQpm77hiKb-RQ#PPA10,M1. 
3. ^ Edward John Routh (2001). A Treatise on Analytical Statics with Numerous Examples. Vol. 2. Adamant Media Corporation. p. 154. ISBN 1402173202. http://books.google.com/books?id=yKmdk4LZxhMC&pg=RA1-PA40&dq=isbn=1402173202&sig=ACfU3U2uhAKDJtIYZEY-Jf-1e5wf7UgG1w#PPA154,M1.  A reprint of the original work published in 1908 by Cambridge University Press.
4. ^ W. W. Rouse Ball A Short Account of the History of Mathematics (4th edition, 1908)
5. ^ Walter William Rouse Ball (1901). A short account of the history of mathematics (3rd ed.). Macmillan. p. 384. http://books.google.com/books?id=O-UGAAAAYAAJ&dq=A+Short+Account+of+the+History+of+Mathematics'+(4th+edition,+1908)+by+W.+W.+Rouse+Ball.&pg=PP1&ots=327JhZ192M&sig=w-HWPhOnc6JAlzlMoralry7rIL4&hl=en&sa=X&oi=book_result&resnum=1&ct=result#PPA384,M1. 
6. ^ Poynting, John Henry; Joseph John Thompson (1907). A Textbook of Physics, 4th Ed.. London: Charles Griffin & Co.. pp. 22–23. http://books.google.com/books?id=TL4KAAAAIAAJ&pg=PA22. 
7. ^ Isaac Todhunter. A History of the Mathematical Theories of Attraction and the Figure of the Earth from the Time of Newton to that of Laplace. Vol. 2. Elibron Classics. ISBN 1402117175. http://books.google.com/books?id=blZ_Tar9IRMC&pg=RA1-PA500&dq=%22Clairaut%27s+theorem%22&lr=&as_brr=0&sig=ACfU3U0BK0IMg4DPZTFon_yf_DyT4wOlcQ#PPA62,M1.  Reprint of the original edition of 1873 published by Macmillan and Co.
8. ^ Osmond Fisher (1889). Physics of the Earth's Crust. Macmillan and Co.. p. 27. http://books.google.com/books?id=o8oPAAAAIAAJ&pg=PA27&dq=%22Clairaut%27s+theorem%22&lr=&as_brr=0. 
9. ^ John Henry Poynting & Joseph John Thomson (1907). A Textbook of Physics. C. Griffin. p. 22. http://books.google.com/books?id=TL4KAAAAIAAJ&pg=PA23&dq=%22Clairaut%27s+theorem%22&lr=&as_brr=0#PPA22,M1. 
10. ^ NASA case file On the equilibrium figure of the earth by Mohammad A. Khan (1968)
11. ^ Eq. 2.57 in MIT Earth Atmospheric and Planetary Sciences OpenCourseWare notes
12. ^ Andrew Pressley (2001). Elementary Differential Geometry. Springer. p. 183. ISBN 1852331526. http://books.google.com/books?id=UXPyquQaO6EC&pg=PA185&dq=%22Clairaut%27s+theorem%22&lr=&as_brr=0&sig=ACfU3U214J0zkWQcRXLTohVjdHUD3Fuk2A#PPA183,M1. 
13. ^ John P. Vinti, Gim J. Der, Nino L. Bonavito (1998). Orbital and Celestial Mechanics. Progress in astronautics and aeronautics, v. 177. American Institute of Aeronautics and Astronautics. p. 171. ISBN 1563472562. http://books.google.com/books?id=-dXzdYHvPgMC&pg=PA172&dq=Earth+spheroid+centrifugal+date:1990-2008&lr=&as_brr=0&sig=ACfU3U0YCa9N8606CejuHyuolKmh56JOtw#PPA171,M1. 
14. ^ Arthur Gordon Webster (1904). The Dynamics of Particles and of Rigid, Elastic, and Fluid Bodies: being lectures on mathematical physics. B.G. Teubner. p. 468. http://books.google.com/books?id=2kMNAAAAYAAJ&printsec=titlepage#PPA468,M1. 
15. ^ Isaac Newton: Principia Book III Proposition XIX Problem III, p. 407 in Andrew Motte translation.
16. ^ See the Principia on line at Andrew Motte Translation
17. ^ Table 1.1 IERS Numerical Standards (2003))
18. ^ Averil B. Chatfield (1997). Fundamentals of High Accuracy Inertial Navigation. Volume 174 in Progress in Astronautics and Aeronautics. American Institute of Aeronautics and Astronautics. Chapter 1, Part VIII p. 7. ISBN 1563472430. http://books.google.com/books?id=2hJTDpT2U1UC&pg=PA1&dq=frame+coordinate+%22state+of+motion%22&lr=&as_brr=0&sig=ACfU3U2NOYvih-VaDyv1CxAkTc7L1AaRXQ#PPA7,M1.