- Displacement (vector)
-
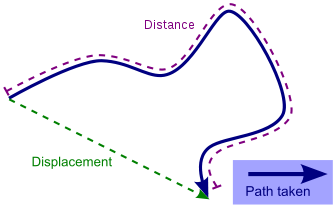
A displacement is the shortest distance from the initial to the final position of a point P[1]. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P. A displacement vector represents the length and direction of that imaginary straight path.
A position vector expresses the position of a point P in space in terms of a displacement from an arbitrary reference point O (typically the origin of a coordinate system). Namely, it indicates both the distance and direction of an imaginary motion along a straight line from the reference position to the actual position of the point.
A displacement may be also described as a relative position: the final position of a point (
 ) relative to its initial position (
) relative to its initial position ( ), and a displacement vector can be mathematically defined as the difference between the final and initial position vectors:
), and a displacement vector can be mathematically defined as the difference between the final and initial position vectors:In considering motions of objects over time the instantaneous velocity of the object is the rate of change of the displacement as a function of time. The velocity then is distinct from the instantaneous speed which is the time rate of change of the distance traveled along a specific path. The velocity may be equivalently defined as the time rate of change of the position vector. If one considers a moving initial position, or equivalenty a moving origin (e.g. an initial position or origin which is fixed to a train wagon, which in turn moves with respect to its rail track), the velocity of P (e.g. a point representing the position of a passenger walking on the train) may be referred to as a relative velocity, as opposed to an absolute velocity, which is computed with respect to a point which is considered to be "fixed in space" (such as, for instance, a point fixed on the floor of the train station).
For motion over a given interval of time, the displacement divided by the length of the time interval defines the average velocity.
Contents
Rigid body
In dealing with the motion of a rigid body, the term displacement may also include the rotations of the body. In this case, the displacement of a particle of the body is called linear displacement (displacement along a line), while the rotation is called angular displacement.
Derivatives
[2] Velocity
Acceleration
Jolt/Jerk/Surge/Lurch
Snap/Jounce
Crackle
Pop/Pounce
Lock
Drop
Where
 is the position vector,
is the position vector,  is the velocity vector,
is the velocity vector,  is the acceleration vector,
is the acceleration vector,  is the jerk vector,
is the jerk vector,  is the snap vector,
is the snap vector,  is the crackle vector,
is the crackle vector,  is the pop vector,
is the pop vector,  is the lock vector, and
is the lock vector, and  is the drop vector.
is the drop vector.See also
Kinematics ← Integrate … Differentiate →
Displacement (Distance) | Velocity (Speed) | Acceleration | Jerk | Jounce
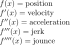
Wikimedia Foundation. 2010.