Angular momentum

For a generally accessible and less technical introduction to the topic, see Introduction to angular momentum.

Classical mechanics
$\mathbf{F} = m \mathbf{a}$ Newton's Second Law
History of classical mechanics · Timeline of classical mechanics
Branches Statics · Dynamics / Kinetics · Kinematics · Applied mechanics · Celestial mechanics · Continuum mechanics · Statistical mechanics
Formulations Newtonian mechanics (Vectorial mechanics) Analytical mechanics: Lagrangian mechanics Hamiltonian mechanics
Fundamental concepts Space · Time · Velocity · Speed · Mass · Acceleration · Gravity · Force · Impulse · Torque / Moment / Couple · Momentum · Angular momentum · Inertia · Moment of inertia · Reference frame · Energy · Kinetic energy · Potential energy · Mechanical work · Virtual work · D'Alembert's principle
Core topics Rigid body · Rigid body dynamics · Euler's equations (rigid body dynamics) · Motion · Newton's laws of motion · Newton's law of universal gravitation · Equations of motion · Inertial frame of reference · Non-inertial reference frame · Rotating reference frame · Fictitious force · Linear motion · Mechanics of planar particle motion · Displacement (vector) · Relative velocity · Friction · Simple harmonic motion · Harmonic oscillator · Vibration · Damping · Damping ratio · Rotational motion · Circular motion · Uniform circular motion · Non-uniform circular motion · Centripetal force · Centrifugal force · Centrifugal force (rotating reference frame) · Reactive centrifugal force · Coriolis force · Pendulum · Rotational speed · Angular acceleration · Angular velocity · Angular frequency · Angular displacement
Scientists Galileo Galilei · Isaac Newton · Jeremiah Horrocks · Leonhard Euler · Jean le Rond d'Alembert · Alexis Clairaut · Joseph Louis Lagrange · Pierre-Simon Laplace · William Rowan Hamilton · Siméon-Denis Poisson
v · d · e

This gyroscope remains upright while spinning due to its angular momentum.

In physics, angular momentum, moment of momentum, or rotational momentum^[1][2] is a conserved vector quantity that can be used to describe the overall state of a physical system. The angular momentum L of a particle with respect to some point of origin is

$\mathbf{L} = \mathbf{r} \times \mathbf{p} = \mathbf{r} \times m\mathbf{v}\, ,$

where r is the particle's position from the origin, p = mv is its linear momentum, and × denotes the cross product.

The angular momentum of a system of particles (e.g. a rigid body) is the sum of angular momenta of the individual particles. For a rigid body rotating around an axis of symmetry (e.g. the fins of a ceiling fan), the angular momentum can be expressed as the product of the body's moment of inertia I (a measure of an object's resistance to changes in its rotation rate) and its angular velocity ω:

$\mathbf{L} = I \boldsymbol{\omega} \, .$

In this way, angular momentum is sometimes described as the rotational analog of linear momentum.

Angular momentum is conserved in a system where there is no net external torque, and its conservation helps explain many diverse phenomena. For example, the increase in rotational speed of a spinning figure skater as the skater's arms are contracted is a consequence of conservation of angular momentum. The very high rotational rates of neutron stars can also be explained in terms of angular momentum conservation. Moreover, angular momentum conservation has numerous applications in physics and engineering (e.g. the gyrocompass).

Angular momentum in classical mechanics

Relationship between force (F), torque (τ), momentum (p), and angular momentum (L) vectors in a rotating system

Definition

The angular momentum L of a particle about a given origin is defined as:

$\mathbf{L}=\mathbf{r}\times\mathbf{p}$

where r is the position vector of the particle relative to the origin, p is the linear momentum of the particle, and × denotes the cross product.

As seen from the definition, the derived SI units of angular momentum are newton meter seconds (N·m·s or kg·m²s⁻¹) or joule seconds. Because of the cross product, L is a pseudovector perpendicular to both the radial vector r and the momentum vector p and it is assigned a sign by the right-hand rule.

For an object with a fixed mass that is rotating about a fixed symmetry axis, the angular momentum is expressed as the product of the moment of inertia of the object and its angular velocity vector:

$\mathbf{L}= I \boldsymbol{\omega}$

where I is the moment of inertia of the object (in general, a tensor quantity), and ω is the angular velocity.

The angular momentum of a particle or rigid body in rectilinear motion (pure translation) is a vector with constant magnitude and direction. If the path of the particle or rigid body passes through the given origin, its angular momentum is zero.

Angular momentum is also known as moment of momentum.

Angular momentum of a collection of particles

If a system consists of several particles, the total angular momentum about a point can be obtained by adding (or integrating) all the angular momenta of the constituent particles.

Angular momentum simplified using the center of mass

It is very often convenient to consider the angular momentum of a collection of particles about their center of mass, since this simplifies the mathematics considerably. The angular momentum of a collection of particles is the sum of the angular momentum of each particle:

$\mathbf{L}=\sum_i \mathbf{R}_i\times m_i \mathbf{V}_i$

where R_i is the position vector of particle i from the reference point, m_i is its mass, and V_i is its velocity. The center of mass is defined by:

$\mathbf{R}=\frac{1}{M}\sum_i m_i \mathbf{R}_i$

where the total mass of all particles is given by

$M=\sum_i m_i.\,$

It follows that the velocity of the center of mass is

$\mathbf{V}=\frac{1}{M}\sum_i m_i \mathbf{V}_i.\,$

If we define r_i as the displacement of particle i from the center of mass, and v_i as the velocity of particle i with respect to the center of mass, then we have

$\mathbf{R}_i=\mathbf{R}+\mathbf{r}_i\,$   and    $\mathbf{V}_i=\mathbf{V}+\mathbf{v}_i\,$

and also

$\sum_i m_i \mathbf{r}_i=0\,$   and    $\sum_i m_i \mathbf{v}_i=0\,$

so that the total angular momentum with respect to the center is

$\mathbf{L}=\sum_i (\mathbf{R}+\mathbf{r}_i)\times m_i (\mathbf{V}+\mathbf{v}_i) = \left(\mathbf{R}\times M\mathbf{V}\right) + \left(\sum_i \mathbf{r}_i\times m_i \mathbf{v}_i\right).$

The first term is just the angular momentum of the center of mass. It is the same angular momentum one would obtain if there were just one particle of mass M moving at velocity V located at the center of mass. The second term is the angular momentum that is the result of the particles moving relative to their center of mass. This second term can be even further simplified if the particles form a rigid body, in which case it is the product of moment of inertia and angular velocity of the spinning motion (as above). The same result is true if the discrete point masses discussed above are replaced by a continuous distribution of matter.

Fixed axis of rotation

Angular momentum in terms of scalar and vector components.

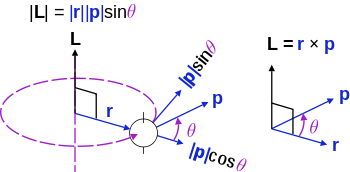
For many applications where one is only concerned about rotation around one axis, it is sufficient to discard the pseudovector nature of angular momentum, and treat it like a scalar where it is positive when it corresponds to a counter-clockwise rotation, and negative clockwise. To do this, just take the definition of the cross product and discard the unit vector, so that angular momentum becomes:

$L = |\mathbf{r}||\mathbf{p}|\sin \theta_{r,p}$

where θ_r,p is the angle between r and p measured from r to p; an important distinction because without it, the sign of the cross product would be meaningless. From the above, it is possible to reformulate the definition to either of the following:

$L = \pm|\mathbf{p}||\mathbf{r}_{\perp}|$

where $\mathbf{r}_{\perp}$ is called the lever arm distance to p.

The easiest way to conceptualize this is to consider the lever arm distance to be the distance from the origin to the line that p travels along. With this definition, it is necessary to consider the direction of p (pointed clockwise or counter-clockwise) to figure out the sign of L. Equivalently:

$L = \pm|\mathbf{r}||\mathbf{p}_{\perp}|$

where $\mathbf{p}_{\perp}$ is the component of p that is perpendicular to r. As above, the sign is decided based on the sense of rotation.

For an object with a fixed mass that is rotating about a fixed symmetry axis, the angular momentum is expressed as the product of the moment of inertia of the object and its angular velocity vector:

$\mathbf{L}= I \boldsymbol{\omega}$

where I is the moment of inertia of the object (in general, a tensor quantity) and ω is the angular velocity.

It is a misconception that angular momentum is always about the same axis as angular velocity. Sometime this may not be possible, in these cases the angular momentum component along the axis of rotation is the product of angular velocity and moment of inertia about the given axis of rotation.

As the kinetic energy K of a massive rotating body is given by

K = Iω² / 2

it is proportional to the square of the angular velocity.

Conservation of angular momentum

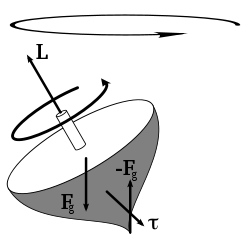The torque caused by the two opposing forces F_g and -F_g causes a change in the angular momentum L in the direction of that torque (since torque is the time derivative of angular momentum). This causes the top to precess.

In a closed system angular momentum is constant. This conservation law mathematically follows from continuous directional symmetry of space (no direction in space is any different from any other direction). See Noether's theorem.^[3]

The time derivative of angular momentum is called torque:

$\boldsymbol{\tau} = \frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t} = \frac{\mathrm{d}\mathbf{r}}{\mathrm{d}t} \times \mathbf{p} + \mathbf{r} \times \frac{\mathrm{d}\mathbf{p}}{\mathrm{d}t} = 0 + \mathbf{r} \times \mathbf{F} = \mathbf{r} \times \mathbf{F}$

(The cross-product of velocity and momentum is zero, because these vectors are parallel.) So requiring the system to be "closed" here is mathematically equivalent to zero external torque acting on the system:

$\mathbf{L}_{\mathrm{system}} = \mathrm{constant} \leftrightarrow \sum \boldsymbol{\tau}_{\mathrm{ext}} = 0$

where $\boldsymbol{\tau}_{ext}$ is any torque applied to the system of particles. It is assumed that internal interaction forces obey Newton's third law of motion in its strong form, that is, that the forces between particles are equal and opposite and act along the line between the particles.

In orbits, the angular momentum is distributed between the spin of the planet itself and the angular momentum of its orbit:

$\mathbf{L}_{\mathrm{total}} = \mathbf{L}_{\mathrm{spin}} + \mathbf{L}_{\mathrm{orbit}}$;

If a planet is found to rotate slower than expected, then astronomers suspect that the planet is accompanied by a satellite, because the total angular momentum is shared between the planet and its satellite in order to be conserved.

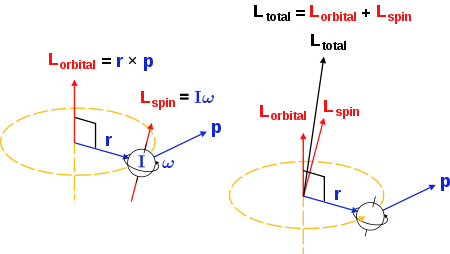Conservation of angular momentum; distributed between the spin and orbital angular momenta. The moment of inertia and angular velocity of the spinning body are about its own spin axes, and its position is radial from the orbital axes and momentum tangential to the curve. Here circular orbits are shown - similar illustrations would follow for an elliptical orbit.

The conservation of angular momentum is used extensively in analyzing what is called central force motion. If the net force on some body is directed always toward some fixed point, the center, then there is no torque on the body with respect to the center, and so the angular momentum of the body about the center is constant. Constant angular momentum is extremely useful when dealing with the orbits of planets and satellites, and also when analyzing the Bohr model of the atom.

The conservation of angular momentum explains the angular acceleration of an ice skater as she brings her arms and legs close to the vertical axis of rotation. By bringing part of mass of her body closer to the axis she decreases her body's moment of inertia. Because angular momentum is constant in the absence of external torques, the angular velocity (rotational speed) of the skater has to increase.

The same phenomenon results in extremely fast spin of compact stars (like white dwarfs, neutron stars and black holes) when they are formed out of much larger and slower rotating stars (indeed, decreasing the size of object 10⁴ times results in increase of its angular velocity by the factor 10⁸).

The conservation of angular momentum in Earth–Moon system results in the transfer of angular momentum from Earth to Moon (due to tidal torque the Moon exerts on the Earth). This in turn results in the slowing down of the rotation rate of Earth (at about 42 nsec/day), and in gradual increase of the radius of Moon's orbit (at ~4.5 cm/year rate).

Angular momentum in relativistic mechanics

In modern (late 20th century) theoretical physics, angular momentum is described using a different formalism. Under this formalism, angular momentum is the 2-form Noether charge associated with rotational invariance (As a result, angular momentum is not conserved for general curved spacetimes, unless it happens to be asymptotically rotationally invariant). For a system of point particles without any intrinsic angular momentum (see below), it turns out to be

$\sum_i \bold{r}_i\wedge \bold{p}_i$

(Here, the wedge product is used.).

In the language of four-vectors and tensors the angular momentum of a particle in relativistic mechanics is expressed as an antisymmetric tensor of second order

$L_{ij} = x_i\ p_j - x_j\ p_i$

Angular momentum in quantum mechanics

In quantum mechanics, angular momentum is quantized – that is, it cannot vary continuously, but only in "quantum leaps" between certain allowed values. The orbital angular momentum of a subatomic particle, that is due to its motion through space, is always a whole-number multiple of $\hbar$ ("h-bar," known as the reduced Planck's constant), which has an appropriate dimension energy·time, or length·momentum. Furthermore, experiments show that most subatomic particles have a permanent, built-in angular momentum, which is not due to their motion through space. This spin angular momentum comes in units of $\hbar/2$. For example, an electron standing at rest has an angular momentum of $\hbar/2$.

Basic definition

The classical definition of angular momentum as $\mathbf{L}=\mathbf{r}\times\mathbf{p}$ depends on six numbers: r_x, r_y, r_z, p_x, p_y, and p_z. Translating this into quantum-mechanical terms, the Heisenberg uncertainty principle tells us that it is not possible for all six of these numbers to be measured simultaneously with arbitrary precision. Therefore, there are limits to what can be known or measured about a particle's angular momentum. It turns out that the best that one can do is to simultaneously measure both the angular momentum vector's magnitude and its component along one axis.

Mathematically, angular momentum in quantum mechanics is defined like momentum – not as a quantity but as an operator on the wave function:

$\mathbf{L}=\mathbf{r}\times\mathbf{p}$

where r and p are the position and momentum operators respectively. In particular, for a single particle with no electric charge and no spin, the angular momentum operator can be written in the position basis as

$\mathbf{L}=-i\hbar(\mathbf{r}\times\nabla)$

where $\nabla$ is the vector differential operator del (also called "nabla"). This orbital angular momentum operator is the most commonly encountered form of the angular momentum operator, though not the only one. It satisfies the following canonical commutation relations:^[4]

$[L_l, L_m ] = i \hbar \sum_{n=1}^{3} \varepsilon_{lmn} L_n$,

where

• ε_lmn is the (antisymmetric) Levi-Civita symbol,
• [X,Y] = XY − YX is the commutator.

From this follows

$\left[L_i, L^2 \right] = 0$

Since,

$L_x = -i\hbar \left(y {\partial\over \partial z} - z {\partial\over \partial y}\right)$

$L_y = -i\hbar \left(z {\partial\over \partial x} - x {\partial\over \partial z}\right)$

$L_z = -i\hbar \left(x {\partial\over \partial y} - y {\partial\over \partial x}\right)$

it follows, for example,

$\begin{align} \left[L_x,L_y\right] & = -\hbar^2 \left( \left(y {\partial \over \partial z} - z {\partial\over \partial y}\right)\left(z {\partial\over \partial x} - x {\partial\over \partial z}\right) - \left(z {\partial\over \partial x} - x {\partial\over \partial z}\right)\left(y {\partial \over \partial z} - z {\partial\over \partial y}\right)\right) \\ & = -\hbar^2 \left( y {\partial\over \partial x} - x {\partial\over \partial y}\right) = i \hbar L_z. \\ \end{align}$

Addition of quantized angular momenta

For more details on this topic, see Clebsch–Gordan coefficients.

Given a quantized total angular momentum $\vec{j}$ which is the sum of two individual quantized angular momenta $\vec{l_1}$ and $\vec{l_2}$,

$\vec{j} = \vec{l_1} + \vec{l_2}$

the quantum number j associated with its magnitude can range from | l₁ − l₂ | to l₁ + l₂ in integer steps where l₁ and l₂ are quantum numbers corresponding to the magnitudes of the individual angular momenta.

Angular momentum as a generator of rotations

If ϕ is the angle around a specific axis, for example the azimuthal angle around the z axis, then the angular momentum along this axis is the generator of rotations around this axis:

$L_z = -i\hbar {\partial\over \partial \phi}.$

The eigenfunctions of L_z are therefore $e^{i m_l \phi}$, and since ϕ has a period of 2π, m_l must be an integer.

For a particle with a spin S, this takes into account only the angular dependence of the location of the particle, for example its orbit in an atom. It is therefore known as orbital angular momentum. However, when one rotates the system, one also changes the spin. Therefore the total angular momentum, which is the full generator of rotations, is J_i = L_i + S_i Being an angular momentum, J satisfies the same commutation relations as L, as will be explained below, namely^[5]

$[J_\ell, J_m ] = i \hbar \sum_{n=1}^{3} \varepsilon_{lmn} J_n$

from which follows

$\left[J_\ell, J^2 \right] = 0.$

Acting with J on the wavefunction ψ of a particle generates a rotation: $e^{i \phi J_z} \psi$ is the wavefunction ψ rotated around the z axis by an angle ϕ. For an infinitesmal rotation by an angle dϕ, the rotated wavefunction is ψ + idϕJ_zψ. This is similarly true for rotations around any axis.

In a charged particle the momentum gets a contribution from the electromagnetic field, and the angular momenta L and J change accordingly.

If the Hamiltonian is invariant under rotations, as in spherically symmetric problems, then according to Noether's theorem, it commutes with the total angular momentum. So the total angular momentum is a conserved quantity

$\left[J_l, H \right] = 0$

Since angular momentum is the generator of rotations, its commutation relations follow the commutation relations of the generators of the three-dimensional rotation group SO(3). This is why J always satisfies these commutation relations. In d dimensions, the angular momentum will satisfy the same commutation relations as the generators of the d-dimensional rotation group SO(d).

SO(3) has the same Lie algebra (i.e. the same commutation relations) as SU(2). Generators of SU(2) can have half-integer eigenvalues, and so can m_j. Indeed for fermions the spin S and total angular momentum J are half-integer. For d=3, in fact, j and m_j always are either integers or half-integers.^[6]

Technically, this is because the universal cover of SO(3) is isomorphic to SU(2), and the representations of the latter are fully known. J_i span the Lie algebra and J² is the Casimir invariant, and it can be shown that if the eigenvalues of J_z and J² are m_j and j(j+1) then m_j and j are both integer multiples of one-half. j is non-negative and m_j takes values between −j and j.

Relation to spherical harmonics

Angular momentum operators usually occur when solving a problem with spherical symmetry in spherical coordinates. Then, the angular momentum in space representation is:

$L^2 = -\frac{\hbar^2}{\sin\theta}\frac{\partial}{\partial \theta}\left( \sin\theta \frac{\partial}{\partial \theta}\right) - \frac{\hbar^2}{\sin^2\theta}\frac{\partial^2}{\partial \phi^2}$

When solving to find eigenstates of this operator, we obtain the following

$L^2 | l, m \rang = {\hbar}^2 l(l+1) | l, m \rang$

$L_z | l, m \rang = \hbar m | l, m \rang$

where

$\lang \theta , \phi | l, m \rang = Y_{l,m}(\theta,\phi)$

are the spherical harmonics.

Thus, a particle whose wave function is the spherical harmonic Y_l,m has an orbital angular momentum

$L = {\hbar} \sqrt{l(l+1)}$

with a z-component

$L_z = {\hbar} m$

Angular momentum in electrodynamics

When describing the motion of a charged particle in the presence of an electromagnetic field, the canonical momentum p is not gauge invariant. As a consequence, the canonical angular momentum $\mathbf{L} = \mathbf{r} \times \mathbf{p}$ is not gauge invariant either. Instead, the momentum that is physical, the so-called kinetic momentum, is

$\mathbf{p} -\frac {e \mathbf{A} }{c}$

where e is the electric charge, c the speed of light and A the vector potential. Thus, for example, the Hamiltonian of a charged particle of mass m in an electromagnetic field is then

$H =\frac{1}{2m} \left( \mathbf{p} -\frac {e \mathbf{A} }{c}\right)^2 + e\phi$

where ϕ is the scalar potential. This is the Hamiltonian that gives the Lorentz force law. The gauge-invariant angular momentum, or "kinetic angular momentum" is given by

$K= \mathbf{r} \times \left( \mathbf{p} -\frac {e \mathbf{A} }{c}\right)$

The interplay with quantum mechanics is discussed further in the article on canonical commutation relations.

See also

• Angular momentum coupling
• Angular momentum of light
• Angular momentum operator
• Areal velocity
• Balancing machine
• Control moment gyroscope
• Falling cat problem
• List of moments of inertia
• Moment of inertia
• Noether's theorem
• Precession
• Relative angular momentum
• Rigid rotor
• Rotational energy
• Spatial quantization
• Specific relative angular momentum
• Spin (physics)
• Yrast

Footnotes

1. ^ Truesdell, Clifford (1991). A First Course in Rational Continuum Mechanics: General concepts. Academic Press. ISBN 0-12-701300-8. http://books.google.com/books?id=l5J3oQ6V5RsC&lpg=PA37&dq=rotational%20momentum&pg=PA37#v=onepage&q=rotational%20momentum&f=false. 
2. ^ Smith, Donald Ray; Truesdell, Clifford (1993). An introduction to continuum mechanics -after Truesdell and Noll. Springer. ISBN 0-7923-2454-4. http://books.google.com/books?id=ZcWC7YVdb4wC&lpg=PP1&pg=PA100#v=onepage&q&f=false. 
3. ^ Landau, L. D.; Lifshitz, E. M. (1995). The classical theory of fields. Course of Theoretical Physics. Oxford, Butterworth-Heinemann. ISBN 0-7506-2768-9. 
4. ^ Aruldhas, G. (2004-02-01). "formula (8.8)". Quantum Mechanics. p. 171. ISBN 9788120319622. http://books.google.com/books?id=dRsvmTFpB3wC&pg=PA171. 
5. ^ Aruldhas, G. (2004-02-01). "eqn (8.20)". Quantum Mechanics. p. 173. ISBN 9788120319622. http://books.google.com/books?id=dRsvmTFpB3wC&pg=PA173. 
6. ^ The same is true for each d>2: j and m_j have to be multiples of ½, but d=2 is a special case.

References

• Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (1977). Quantum Mechanics. John Wiley & Sons. 
• Condon, E. U.; Shortley, G. H. (1935). "Esp. chpt. 3". The Theory of Atomic Spectra. Cambridge University Press. ISBN 0-521-09209-4. 
• Edmonds, A. R. (1957). Angular Momentum in Quantum Mechanics. Princeton University Press. ISBN 0-691-07912-9. 
• Jackson, John David (1998). Classical Electrodynamics (3rd ed.). John Wiley & Sons. ISBN 978-0-471-30932-1. 
• Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers, 6th ed.. Brooks/Cole. ISBN 0-534-40842-7. 
• Thompson, William J. (1994). Angular Momentum: An Illustrated Guide to Rotational Symmetries for Physical Systems. Wiley. ISBN 0-471-55264-X. 
• Tipler, Paul (2004). Physics for Scientists and Engineers: Mechanics, Oscillations and Waves, Thermodynamics, 5th ed.. W. H. Freeman. ISBN 0-7167-0809-4. 

External links

• Conservation of Angular Momentum - a chapter from an online textbook
• Angular Momentum in a Collision Process - derivation of the three dimensional case