Damping

Classical mechanics
$\mathbf{F} = m \mathbf{a}$ Newton's Second Law
History of classical mechanics · Timeline of classical mechanics
Branches Statics · Dynamics / Kinetics · Kinematics · Applied mechanics · Celestial mechanics · Continuum mechanics · Statistical mechanics
Formulations Newtonian mechanics (Vectorial mechanics) Analytical mechanics: Lagrangian mechanics Hamiltonian mechanics
Fundamental concepts Space · Time · Velocity · Speed · Mass · Acceleration · Gravity · Force · Impulse · Torque / Moment / Couple · Momentum · Angular momentum · Inertia · Moment of inertia · Reference frame · Energy · Kinetic energy · Potential energy · Mechanical work · Virtual work · D'Alembert's principle
Core topics Rigid body · Rigid body dynamics · Euler's equations (rigid body dynamics) · Motion · Newton's laws of motion · Newton's law of universal gravitation · Euler's laws of motion · Equations of motion · Inertial frame of reference · Non-inertial reference frame · Rotating reference frame · Fictitious force · Linear motion · Mechanics of planar particle motion · Displacement (vector) · Relative velocity · Friction · Simple harmonic motion · Harmonic oscillator · Vibration · Damping · Damping ratio · Rotational motion · Circular motion · Uniform circular motion · Non-uniform circular motion · Centripetal force · Centrifugal force · Centrifugal force (rotating reference frame) · Reactive centrifugal force · Coriolis force · Pendulum · Rotational speed · Angular acceleration · Angular velocity · Angular frequency · Angular displacement
Scientists Galileo Galilei · Isaac Newton · Jeremiah Horrocks · Leonhard Euler · Jean le Rond d'Alembert · Alexis Clairaut · Joseph Louis Lagrange · Pierre-Simon Laplace · William Rowan Hamilton · Siméon-Denis Poisson
v · d · e

Damped spring–mass system

This article is about damped harmonic oscillators. For detailed mathematical description of the harmonic oscillator including forcing and damping, see Harmonic oscillator. For damping in music, see Damping (music).

In physics, damping is any effect that tends to reduce the amplitude of oscillations in an oscillatory system, particularly the harmonic oscillator.

In mechanics, friction is one such damping effect. For many purposes the frictional force F_f can be modeled as being proportional to the velocity v of the object:

$F_{\mathrm f} = -c v \, ,$

where c is the viscous damping coefficient, given in units of newton seconds per meter (N s/m) or simply kilograms per second.

Generally, damped harmonic oscillators satisfy the second-order differential equation:

$\frac{d^2x}{dt^2} + 2\zeta\omega_0\frac{dx}{dt} + \omega_0^2 x = 0,$

where ω₀ is the undamped angular frequency of the oscillator and ζ is a constant called the damping ratio.

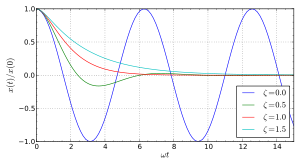
The value of the damping ratio ζ determines the behavior of the system. A damped harmonic oscillator can be:

• Overdamped (ζ > 1): The system returns (exponentially decays) to equilibrium without oscillating. Larger values of the damping ratio ζ return to equilibrium slower.
• Critically damped (ζ = 1): The system returns to equilibrium as quickly as possible without oscillating. This is often desired for the damping of systems such as doors.
• Underdamped (0 < ζ < 1): The system oscillates (at reduced frequency compared to the undamped case) with the amplitude gradually decreasing to zero.
• Undamped (ζ = 0): The system oscillates at its natural resonant frequency (ω_o).

Definition

In physics and engineering, damping may be mathematically modelled as a force synchronous with the velocity of the object but opposite in direction to it. If such force is also proportional to the velocity, as for a simple mechanical viscous damper (dashpot), the force F may be related to the velocity v by

$F = -cv \, ,$

where c is the viscous damping coefficient, given in units of newton-seconds per meter.

This force is an approximation to the friction caused by drag.

This relationship is perfectly analogous to electrical resistance as described by Ohm's law.

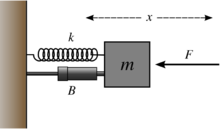
Example: mass–spring–damper

A mass attached to a spring and damper. The damping coefficient, usually c, is represented by B in this case. The F in the diagram denotes an external force, which this example does not include.

An ideal mass–spring–damper system with mass m, spring constant k and viscous damper of damping coefficient c is subject to an oscillatory force

$F_\mathrm{s} = - k x \,$

and a damping force

$F_\mathrm{d} = - c v = - c \frac{dx}{dt} = - c \dot{x}.$

The values can be in any consistent system of units; for example, in SI units, m in kilograms, k in newtons per meter, and c in newton-seconds per meter or kilograms per second.

Treating the mass as a free body and applying Newton's second law, the total force F_tot on the body is

$F_\mathrm{tot} = ma = m \frac{d^2x}{dt^2} = m \ddot{x}.$

where a is the acceleration of the mass and x is the displacement of the mass relative to a fixed point of reference.

Since F_tot = F_s + F_d,

$m \ddot{x} = -kx + -c\dot{x}.$

This differential equation may be rearranged into

$\ddot{x} + { c \over m} \dot{x} + {k \over m} x = 0.\,$

The following parameters are then defined:

$\omega_0 = \sqrt{ k \over m }$

$\zeta = { c \over 2 \sqrt{m k} }.$

The first parameter, ω₀, is called the (undamped) natural frequency of the system . The second parameter, ζ, is called the damping ratio. The natural frequency represents an angular frequency, expressed in radians per second. The damping ratio is a dimensionless quantity.

The differential equation now becomes

$\ddot{x} + 2 \zeta \omega_0 \dot{x} + \omega_0^2 x = 0.\,$

Continuing, we can solve the equation by assuming a solution x such that:

$x = e^{\gamma t}\,$

where the parameter γ (gamma) is, in general, a complex number.

Substituting this assumed solution back into the differential equation gives

$\gamma^2 + 2 \zeta \omega_0 \gamma + \omega_0^2 = 0 \, ,$

which is the characteristic equation.

Solving the characteristic equation will give two roots, γ₊ and γ₋. The solution to the differential equation is thus^[1]

$x(t) = Ae^{\gamma_+ t} + Be^{\gamma_- t} \, ,$

where A and B are determined by the initial conditions of the system:

$A = x(0)+\frac{\gamma_+x(0)-\dot{x}(0)}{\gamma_--\gamma_+}$

$B = -\frac{\gamma_+x(0)-\dot{x}(0)}{\gamma_--\gamma_+}.$

System behavior

Dependence of the system behavior on the value of the damping ratio ζ, for undamped (blue), under-damped (green), critically damped (red), and over-damped (cyan) cases, for zero-velocity initial condition.

The behavior of the system depends on the relative values of the two fundamental parameters, the natural frequency ω₀ and the damping ratio ζ. In particular, the qualitative behavior of the system depends crucially on whether the quadratic equation for γ has one real solution, two real solutions, or two complex conjugate solutions.

Critical damping (ζ = 1)

When ζ = 1, there is a double root γ (defined above), which is real. The system is said to be critically damped. A critically damped system converges to zero as fast as possible without oscillating. An example of critical damping is the door closer seen on many hinged doors in public buildings. The recoil mechanisms in most guns are also critically damped so that they return to their original position, after the recoil due to firing, in the least possible time.

In this case, with only one root γ, there is in addition to the solution x(t) = e^γt a solution x(t) = te^γt:^[2]

$x(t) = (A+Bt)\,e^{-\omega_0 t} \,$

where A and B are determined by the initial conditions of the system (usually the initial position and velocity of the mass):

$A = x(0) \,$

$B = \dot{x}(0)+\omega_0x(0) \,$

Over-damping (ζ > 1)

When ζ > 1, the system is over-damped and there are two different real roots. An over-damped door-closer will take longer to close than a critically damped door would.

The solution to the motion equation is^[3]:

$x(t) = Ae^{\gamma_+ t} + Be^{\gamma_- t}$

where A and B are determined by the initial conditions of the system:

$A = x(0)+\frac{\gamma_+x(0)-\dot{x}(0)}{\gamma_--\gamma_+}$

$B = -\frac{\gamma_+x(0)-\dot{x}(0)}{\gamma_--\gamma_+}.$

Under-damping (0 ≤ ζ < 1)

Finally, when 0 ≤ ζ < 1, γ is complex, and the system is under-damped. In this situation, the system will oscillate at the natural damped frequency ω_d, which is a function of the natural frequency and the damping ratio. To continue the analogy, an underdamped door closer would close quickly, but would hit the door frame with significant velocity, or would oscillate in the case of a swinging door.

In this case, the solution can be generally written as^[4]:

$x (t) = e^{- \zeta \omega_0 t} (A \cos\,(\omega_\mathrm{d}\,t) + B \sin\,(\omega_\mathrm{d}\,t ))\,$

where

$\omega_\mathrm{d} = \omega_0 \sqrt{1 - \zeta^2 }\,$

represents the damped frequency or ringing frequency of the system,^[5] and A and B are again determined by the initial conditions of the system:

$A = x(0)\,$

$B = \frac{1}{\omega_\mathrm{d}}(\zeta\omega_0x(0)+\dot{x}(0)).\,$

This "damped frequency" is not to be confused with the damped resonant frequency or peak frequency ω_peak.^[6] This is the frequency at which a moderately underdamped (ζ < 1/√2) simple 2nd-order harmonic oscillator has its maximum gain (or peak transmissibility) when driven by a sinusoidal input. The frequency at which this peak occurs is given by:

$\omega_{peak} = \omega_0\sqrt{1 - 2\zeta^2}.$

For an under-damped system, the value of ζ can be found by examining the logarithm of the ratio of succeeding amplitudes of a system. This is called the logarithmic decrement.

Alternative models

Viscous damping models, although widely used, are not the only damping models. A wide range of models can be found in specialized literature, but one of them should be referred here: the so called "hysteretic damping model" or "structural damping model".

When a metal beam is vibrating, the internal damping can be better described by a force proportional to the displacement but in phase with the velocity. In such case, the differential equation that describes the free movement of a single-degree-of-freedom system becomes:

$m \ddot{x} + h x i + k x = 0$

where h is the hysteretic damping coefficient and i denotes the imaginary unit; the presence of i is required to synchronize the damping force to the velocity (xi being in phase with the velocity). This equation is more often written as:

$m \ddot{x} + k ( 1 + i \eta ) x = 0$

where η is the hysteretic damping ratio, that is, the fraction of energy lost in each cycle of the vibration.

Although requiring complex analysis to solve the equation, this model reproduces the real behaviour of many vibrating structures more closely than the viscous model.

A more general model that also requires complex analysis, the fractional model not only includes both the viscous and hysteretic models, but also allows for intermediate cases (useful for some polymers):

$m \ddot{x} + A \frac{d^r x}{dt^r} i + k x = 0$

where r is any number, usually between 0 (for hysteretic) and 1 (for viscous), and A is a general damping (h for hysteretic and c for viscous) coefficient.

See also: Friction and Drag

See also

• Damping ratio
• Damping factor
• RLC circuit
• Oscillator
• Harmonic oscillator
• Simple harmonic motion
• Resonance
• Impulse excitation technique
• Audio system measurements
• Thermoelastic damping
• Tuned mass damper
• Vehicle suspension
• Vibration
• Vibration control
• Thrust damping
• Particle damping

References

1. ^ MathWorld--A Wolfram Web Resource. [1]
2. ^ Weisstein, Eric W. "Damped Simple Harmonic Motion--Critical Damping." From MathWorld--A Wolfram Web Resource. [2]
3. ^ Weisstein, Eric W., "Damped Simple Harmonic Motion--Overdamping." from MathWorld.
4. ^ Weisstein, Eric W. "Damped Simple Harmonic Motion--Underdamping." From MathWorld--A Wolfram Web Resource. [3]
5. ^ Lincoln D. Jones (2003). Electrical Engineering License Review (8th ed.). Dearborn Trade Publishing. p. 6-15. ISBN 9780793185290. http://books.google.com/books?id=9QXpWQqlwNQC&pg=PT174. 
6. ^ Millard F. Beatty (2006). Principles of engineering mechanics. Birkhäuser. p. 167. ISBN 9780387237046. http://books.google.com/books?id=k4GgsitYDt4C&pg=PA167. 

Books

Komkov, Vadim (1972) Optimal control theory for the damping of vibrations of simple elastic systems. Lecture Notes in Mathematics, Vol. 253. Springer-Verlag, Berlin-New York.

External links

• Calculation of the matching attenuation,the damping factor, and the damping of bridging