Atomic radius

Diagram of a helium atom, showing the electron probability density as shades of gray.

The atomic radius of a chemical element is a measure of the size of its atoms, usually the mean or typical distance from the nucleus to the boundary of the surrounding cloud of electrons. Since the boundary is not a well-defined physical entity, there are various non-equivalent definitions of atomic radius.

Depending on the definition, the term may apply only to isolated atoms, or also to atoms in condensed matter, covalently bound in molecules, or in ionized and excited states; and its value may be obtained through experimental measurements, or computed from theoretical models. Under some definitions, the value of the radius may depend on the atom's state and context.^[1]

The concept is difficult to define because the electrons do not have definite orbits, or sharply defined ranges. Rather, their positions must be described as probability distributions that taper off gradually as one moves away from the nucleus, without a sharp cutoff. Moreover, in condensed matter and molecules, the electron clouds of the atoms usually overlap to some extent, and some of the electrons may roam over a large region encompassing two or more atoms.

Despite these conceptual difficulties, under most definitions the radii of isolated neutral atoms range between 30 and 300 pm (trillionths of a meter), or between 0.3 and 3 angstroms. Therefore, the radius of an atom is more than 10,000 times the radius of its nucleus (1–10 fm),^[2] and less than 1/1000 of the wavelength of visible light (400–700 nm).

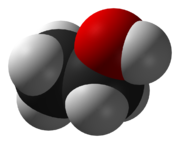The approximate shape of a molecule of ethanol, CH₃CH₂OH. Each atom is modeled by a sphere with the element's Van der Waals radius.

For many purposes, atoms can be modeled as spheres. This is only a crude approximation, but it can provide quantitative explanations and predictions for many phenomena, such as the density of liquids and solids, the diffusion of fluids through molecular sieves, the arrangement of atoms and ions in crystals, and the size and shape of molecules.^{[citation needed]}

Atomic radii vary in a predictable and explicable manner across the periodic table. For instance, the radii generally decrease along each period (row) of the table, from the alkali metals to the noble gases; and increase down each group (column). The radius increases sharply between the noble gas at the end of each period and the alkali metal at the beginning of the next period. These trends of the atomic radii (and of various other chemical and physical properties of the elements) can be explained by the electron shell theory of the atom; they provided important evidence for the development and confirmation of quantum theory.

History

In 1920, shortly after it had become possible to determine the sizes of atoms using X-ray crystallography, it was suggested that all atoms of the same element have the same radii.^[3] However, in 1923, when more crystal data had become available, it was found that an atom does not have just one size. For example, the size of lithium atoms is different in lithium metal than in LiCl.^[4]

Definitions

Widely used definitions of atomic radius include:

• Van der Waals radius: in principle, half the minimum distance between the nuclei of two atoms of the element that are not bound to the same molecule.^[5]
• Ionic radius: the nominal radius of the ions of an element in a specific ionization state, deduced from the spacing of atomic nuclei in crystalline salts that include that ion. In principle, the spacing between two adjacent oppositely charged ions (the length of the ionic bond between them) should equal the sum of their ionic radii.^[5]
• Covalent radius: the nominal radius of the atoms of an element when covalently bound to other atoms, as deduced the separation between the atomic nuclei in molecules. In principle, the distance between two atoms that are bound to each other in a molecule (the length of that covalent bond) should equal the sum of their covalent radii.^[5]
• Metallic radius: the nominal radius of atoms of an element when joined to other atoms by metallic bonds.^{[citation needed]}
• Bohr radius: the radius of the lowest-energy electron orbit predicted by Bohr model of the atom (1913).^[6][7] It is only applicable to atoms and ions with a single electron, such as hydrogen, singly ionized helium, and positronium. Although the model itself is now obsolete, the Bohr radius for the hydrogen atom is still regarded as an important physical constant.

Empirically measured atomic radii

The following table shows empirically measured covalent radii for the elements, as published by J. C. Slater in 1964.^[8] The values are in picometers (pm), with an accuracy of about 5 pm. The shade of the box ranges from red to yellow as the radius increases; gray indicates lack of data.

Group (vertical)

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

Period (horizontal)

1

H 25

He

2

Li 145

Be 105

B 85

C 70

N 65

O 60

F 50

Ne

3

Na 180

Mg 150

Al 125

Si 110

P 100

S 100

Cl 100

Ar

4

K 220

Ca 180

Sc 160

Ti 140

V 135

Cr 140

Mn 140

Fe 140

Co 135

Ni 135

Cu 135

Zn 135

Ga 130

Ge 125

As 115

Se 115

Br 115

Kr

5

Rb 235

Sr 200

Y 180

Zr 155

Nb 145

Mo 145

Tc 135

Ru 130

Rh 135

Pd 140

Ag 160

Cd 155

In 155

Sn 145

Sb 145

Te 140

I 140

Xe

6

Cs 260

Ba 215

*

Hf 155

Ta 145

W 135

Re 135

Os 130

Ir 135

Pt 135

Au 135

Hg 150

Tl 190

Pb 180

Bi 160

Po 190

At

Rn

7

Fr

Ra 215

**

Rf

Db

Sg

Bh

Hs

Mt

Ds

Rg

Cn

Uut

Uuq

Uup

Uuh

Uus

Uuo

Lanthanides

*

La 195

Ce 185

Pr 185

Nd 185

Pm 185

Sm 185

Eu 185

Gd 180

Tb 175

Dy 175

Ho 175

Er 175

Tm 175

Yb 175

Lu 175

Actinides

**

Ac 195

Th 180

Pa 180

U 175

Np 175

Pu 175

Am 175

Cm

Bk

Cf

Es

Fm

Md

No

Lr

Explanation of the general trends

The way the atomic radius varies with increasing atomic number can be explained by the arrangement of electrons in shells of fixed capacity. The shells are generally filled in order of increasing radius, since the negatively charged electrons are attracted by the positively charged protons in the nucleus. As the atomic number increases along each row of the periodic table, the additional electrons go into the same outermost shell; whose radius gradually contracts, due to the increasing nuclear charge. In a noble gas, the outermost shell is completely filled; therefore, the additional electron of next alkali metal will go into the next outer shell, accounting for the sudden increase in the atomic radius.

The increasing nuclear charge is partly counterbalanced by the increasing number of electrons, a phenomenon that is known as shielding; which explains why the size of atoms usually increases down each column. However, there are two occasions where shielding is less effective: in these cases, the atoms are smaller than would otherwise be expected.^{[clarification needed]}

The following table summarizes the main phenomena that influence the atomic radius of an element:

factor	principle	increase with...	tend to	effect on radius
electron shells	quantum mechanics	principal and azimuthal quantum numbers	increase atomic radius	increases down each column
nuclear charge	attractive force acting on electrons by protons in nucleus	atomic number	decrease atomic radius	decreases along each period
shielding	repulsive force acting on outermost shell electrons by inner electrons	number of electron shells	increase atomic radius	reduces the effect of the 2nd factor

Lanthanide contraction

Main article: Lanthanide contraction

The electrons in the 4f-subshell, which is progressively filled from cerium (Z = 58) to lutetium (Z = 71), are not particularly effective at shielding the increasing nuclear charge from the sub-shells further out. The elements immediately following the lanthanides have atomic radii which are smaller than would be expected and which are almost identical to the atomic radii of the elements immediately above them.^[9] Hence hafnium has virtually the same atomic radius (and chemistry) as zirconium, and tantalum has an atomic radius similar to niobium, and so forth. The effect of the lanthanide contraction is noticeable up to platinum (Z = 78), after which it is masked by a relativistic effect known as the inert pair effect.

Due to lanthanide contraction, the 5 following observations can be drawn:

1. The size of Ln³⁺ ions regularly decreases with atomic number. According to Fajans' rules, decrease in size of Ln³⁺ ions increases the covalent character and decreases the basic character between Ln³⁺ and OH⁻ ions in Ln(OH)₃. Hence the order of size of Ln³⁺ is given:
   La³⁺ > Ce³⁺ > ... , ... > Lu³⁺.
2. There is a regular decrease in their ionic radii.
3. There is a regular decrease in their tendency to act as a reducing agent, with increase in atomic number.
4. The second and third rows of d-block transition elements are quite close in properties.
5. Consequently, these elements occur together in natural minerals and are difficult to separate.

d-Block contraction

Main article: d-block contraction

The d-block contraction is less pronounced than the lanthanide contraction but arises from a similar cause. In this case, it is the poor shielding capacity of the 3d-electrons which affects the atomic radii and chemistries of the elements immediately following the first row of the transition metals, from gallium (Z = 31) to bromine (Z = 35).^[9]

Calculated atomic radii

The following table shows atomic radii computed from theoretical models, as published by Enrico Clementi and others in 1967.^[10] The values are in picometres (pm).

Group (vertical)

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

Period (horizontal)

1

H 53

He 31

2

Li 167

Be 112

B 87

C 67

N 56

O 48

F 42

Ne 38

3

Na 190

Mg 145

Al 118

Si 111

P 98

S 88

Cl 79

Ar 71

4

K 243

Ca 194

Sc 184

Ti 176

V 171

Cr 166

Mn 161

Fe 156

Co 152

Ni 149

Cu 145

Zn 142

Ga 136

Ge 125

As 114

Se 103

Br 94

Kr 88

5

Rb 265

Sr 219

Y 212

Zr 206

Nb 198

Mo 190

Tc 183

Ru 178

Rh 173

Pd 169

Ag 165

Cd 161

In 156

Sn 145

Sb 133

Te 123

I 115

Xe 108

6

Cs 298

Ba 253

*

Hf 208

Ta 200

W 193

Re 188

Os 185

Ir 180

Pt 177

Au 174

Hg 171

Tl 156

Pb 154

Bi 143

Po 135

At

Rn 120

7

Fr

Ra

**

Rf

Db

Sg

Bh

Hs

Mt

Ds

Rg

Cn

Uut

Uuq

Uup

Uuh

Uus

Uuo

Lanthanides

*

La

Ce

Pr 247

Nd 206

Pm 205

Sm 238

Eu 231

Gd 233

Tb 225

Dy 228

Ho

Er 226

Tm 222

Yb 222

Lu 217

Actinides

**

Ac

Th

Pa

U

Np

Pu

Am

Cm

Bk

Cf

Es

Fm

Md

No

Lr

See also

• Atomic radii of the elements (data page)
• Chemical bond
• Covalent radius
• Bond length
• Steric hindrance

References

1. ^ Cotton, F. A.; Wilkinson, G. (1988). Advanced Inorganic Chemistry (5th ed.). Wiley. p. 1385. ISBN 978-0-471-84997-1. 
2. ^ Basdevant, J.-L.; Rich, J.; Spiro, M. (2005). Fundamentals in Nuclear Physics. Springer. p. 13, fig 1.1. ISBN 978-0-387-01672-6. http://books.google.com/?id=OFx7P9mgC9oC&pg=PA375&dq=helium+%22nuclear+structure%22#PPA13,M1. 
3. ^ Bragg, W. L. (1920). "The arrangement of atoms in crystals". Philosophical Magazine. 6 40 (236): 169–189. 
4. ^ Wyckoff, R. W. G. (1923). "On the Hypothesis of Constant Atomic Radii". Proceedings of the National Academy of Sciences of the United States of America 9 (2): 33–38. Bibcode 1923PNAS....9...33W. doi:10.1073/pnas.9.2.33. PMC 1085234. PMID 16576657. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=1085234. 
5. ^ ^{a b c} Pauling, L. (1945). The Nature of the Chemical Bond (2nd ed.). Cornell University Press. LCCN 42034474. 
6. ^ Bohr, N. (1913). "On the Constitution of Atoms and Molecules, Part I. – Binding of Electrons by Positive Nuclei". Philosophical Magazine. 6 26 (151): 1–24. http://web.ihep.su/dbserv/compas/src/bohr13/eng.pdf. Retrieved 8 June 2011. 
7. ^ Bohr, N. (1913). "On the Constitution of Atoms and Molecules, Part II. – Systems containing only a Single Nucleus". Philosophical Magazine. 6 26 (153): 476–502. http://web.ihep.su/dbserv/compas/src/bohr13b/eng.pdf. Retrieved 8 June 2011. 
8. ^ Slater, J. C. (1964). "Atomic Radii in Crystals". Journal of Chemical Physics 41 (10): 3199–3205. Bibcode 1964JChPh..41.3199S. doi:10.1063/1.1725697. 
9. ^ ^{a b} Jolly, W. L. (1991). Modern Inorganic Chemistry (2nd ed.). McGraw-Hill. p. 22. ISBN 978-0-0711-2651-9. 
10. ^ Clementi, E.; Raimond, D. L.; Reinhardt, W. P. (1967). "Atomic Screening Constants from SCF Functions. II. Atoms with 37 to 86 Electrons". Journal of Chemical Physics 47 (4): 1300–1307. Bibcode 1967JChPh..47.1300C. doi:10.1063/1.1712084.