- Odds ratio
-
The odds ratio [1][2][3] is a measure of effect size, describing the strength of association or non-independence between two binary data values. It is used as a descriptive statistic, and plays an important role in logistic regression. Unlike other measures of association for paired binary data such as the relative risk, the odds ratio treats the two variables being compared symmetrically, and can be estimated using some types of non-random samples.
Definition
Definition in terms of group-wise odds
The odds ratio is the ratio of the odds of an event occurring in one group to the odds of it occurring in another group. The term is also used to refer to sample-based estimates of this ratio. These groups might be men and women, an experimental group and a control group, or any other dichotomous classification. If the probabilities of the event in each of the groups are p1 (first group) and p2 (second group), then the odds ratio is:
where qx = 1 − px. An odds ratio of 1 indicates that the condition or event under study is equally likely to occur in both groups. An odds ratio greater than 1 indicates that the condition or event is more likely to occur in the first group. And an odds ratio less than 1 indicates that the condition or event is less likely to occur in the first group. The odds ratio must be nonnegative if it is defined. It is undefined if p2q1 equals zero, i.e., if p2 equals zero or p1 equals one.
Definition in terms of joint and conditional probabilities
The odds ratio can also be defined in terms of the joint probability distribution of two binary random variables. The joint distribution of binary random variables X and Y can be written
Y = 1 Y = 0 X = 1 p11 p10 X = 0 p01 p00 where p11, p10, p01 and p00 are non-negative "cell probabilities" that sum to one. The odds for Y within the two subpopulations defined by X = 1 and X = 0 are defined in terms of the conditional probabilities given X:
Y = 1 Y = 0 X = 1 p11 / (p11 + p10) p10 / (p11 + p10) X = 0 p01 / (p01 + p00) p00 / (p01 + p00) Thus the odds ratio is
The simple expression on the right, above, is easy to remember as the product of the probabilities of the "concordant cells" (X = Y) divided by the product of the probabilities of the "discordant cells" (X ≠ Y). However note that in some applications the labeling of categories as zero and one is arbitrary, so there is nothing special about concordant versus discordant values in these applications.
Symmetry
If we had calculated the odds ratio based on the conditional probabilities given Y,
Y = 1 Y = 0 X = 1 p11 / (p11 + p01) p10 / (p10 + p00) X = 0 p01 / (p11 + p01) p00 / (p10 + p00) we would have gotten the same result
Other measures of effect size for binary data such as the relative risk do not have this symmetry property.
Relation to statistical independence
If X and Y are independent, their joint probabilities can be expressed in terms of their marginal probabilities px = P(X = 1) and py = P(Y = 1), as follows
Y = 1 Y = 0 X = 1 pxpy px(1 − py) X = 0 (1 − px)py (1 − px)(1 − py) In this case, the odds ratio equals one, and conversely the odds ratio can only equal one if the joint probabilities can be factored in this way. Thus the odds ratio equals one if and only if X and Y are independent.
Recovering the cell probabilities from the odds ratio and marginal probabilities
The odds ratio is a function of the cell probabilities, and conversely, the cell probabilities can be recovered given knowledge of the odds ratio and the marginal probabilities P(X = 1) = p11 + p10 and P(Y = 1) = p11 + p01. If the odds ratio R differs from 1, then
where p1• = p11 + p10, p•1 = p11 + p01, and
In the case where R = 1, we have independence, so p11 = p1•p•1.
Once we have p11, the other three cell probabilities can easily be recovered from the marginal probabilities.
Example
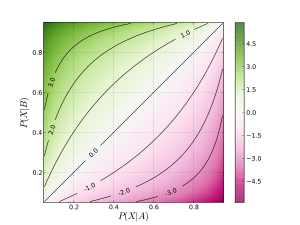 A graph showing how the log odds ratio relates to the underlying probabilities of the outcome X occurring in two groups, denoted A and B. The log odds ratio shown here is based on the odds for the event occurring in group B relative to the odds for the event occurring in group A. Thus, when the probability of X occurring in group B is greater than the probability of X occurring in group A, the odds ratio is greater than 1, and the log odds ratio is greater than 0.
A graph showing how the log odds ratio relates to the underlying probabilities of the outcome X occurring in two groups, denoted A and B. The log odds ratio shown here is based on the odds for the event occurring in group B relative to the odds for the event occurring in group A. Thus, when the probability of X occurring in group B is greater than the probability of X occurring in group A, the odds ratio is greater than 1, and the log odds ratio is greater than 0.
Suppose that in a sample of 100 men, 90 drank wine in the previous week, while in a sample of 100 women only 20 drank wine in the same period. The odds of a man drinking wine are 90 to 10, or 9:1, while the odds of a woman drinking wine are only 20 to 80, or 1:4 = 0.25:1. The odds ratio is thus 9/0.25, or 36, showing that men are much more likely to drink wine than women. The detailed calculation is:
This example also shows how odds ratios are sometimes sensitive in stating relative positions: in this sample men are 90/20 = 4.5 times more likely to have drunk wine than women, but have 36 times the odds. The logarithm of the odds ratio, the difference of the logits of the probabilities, tempers this effect, and also makes the measure symmetric with respect to the ordering of groups. For example, using natural logarithms, an odds ratio of 36/1 maps to 3.584, and an odds ratio of 1/36 maps to −3.584.
Statistical inference
 A graph showing the minimum value of the sample log odds ratio statistic that must be observed to be deemed significant at the 0.05 level, for a given sample size. The three lines correspond to different settings of the marginal probabilities in the 2x2 contingency table (the row and column marginal probabilities are equal in this graph).
A graph showing the minimum value of the sample log odds ratio statistic that must be observed to be deemed significant at the 0.05 level, for a given sample size. The three lines correspond to different settings of the marginal probabilities in the 2x2 contingency table (the row and column marginal probabilities are equal in this graph).
Several approaches to statistical inference for odds ratios have been developed.
One approach to inference uses large sample approximations to the sampling distribution of the log odds ratio (the natural logarithm of the odds ratio). If we use the joint probability notation defined above, the population log odds ratio is
If we observe data in the form of a contingency table
Y = 1 Y = 0 X = 1 n11 n10 X = 0 n01 n00 then the probabilities in the joint distribution can be estimated as
Y = 1 Y = 0 X = 1 

X = 0 

where p̂ = nij / n, with n = n11 + n10 + n01 + n00 being the sum of all four cell counts. The sample log odds ratio is
 .
.
The distribution of the log odds ratio is approximately normal with:

The standard error for the log odds ratio is approximately
 .
.
This is an asymptotic approximation, and will not give a meaningful result if any of the cell counts are very small. If L is the sample log odds ratio, an approximate 95% confidence interval for the population log odds ratio is L ± 1.96SE.[4] This can be mapped to exp(L − 1.96SE), exp(L + 1.96SE) to obtain a 95% confidence interval for the odds ratio. If we wish to test the hypothesis that the population odds ratio equals one, the two-sided p-value is 2P(Z< −|L|/SE), where P denotes a probability, and Z denotes a standard normal random variable.
An alternative approach to inference for odds ratios looks at the distribution of the data conditionally on the marginal frequencies of X and Y. An advantage of this approach is that the sampling distribution of the odds ratio can be expressed exactly.
Role in logistic regression
Logistic regression is one way to generalize the odds ratio beyond two binary variables. Suppose we have a binary response variable Y and a binary predictor variable X, and in addition we have other predictor variables Z1, ..., Zp that may or may not be binary. If we use multiple logistic regression to regress Y on X, Z1, ..., Zp, then the estimated coefficient
 for X is related to a conditional odds ratio. Specifically, at the population level
for X is related to a conditional odds ratio. Specifically, at the population levelso
 is an estimate of this conditional odds ratio. The interpretation of
is an estimate of this conditional odds ratio. The interpretation of  is as an estimate of the odds ratio between Y and X when the values of Z1, ..., Zp are held fixed.
is as an estimate of the odds ratio between Y and X when the values of Z1, ..., Zp are held fixed.Insensitivity to the type of sampling
If the data form a "population sample", then the cell probabilities p̂ij are interpreted as the frequencies of each of the four groups in the population as defined by their X and Y values. In many settings it is impractical to obtain a population sample, so a selected sample is used. For example, we may choose to sample units with X = 1 with a given probability f, regardless of their frequency in the population (which would necessitate sampling units with X = 0 with probability 1 − f). In this situation, our data would follow the following joint probabilities:
Y = 1 Y = 0 X = 1 fp11 / (p11 + p10) fp10(p11 + p10) X = 0 (1 − f)p01 / (p01 + p00) (1 − f)p00 / (p01 + p00) The odds ratio p11p00 / p01p10 for this distribution does not depend on the value of f. This shows that the odds ratio (and consequently the log odds ratio) is invariant to non-random sampling based on one of the variables being studied. Note however that the standard error of the log odds ratio does depend on the value of f. This fact is exploited in two important situations:
- Suppose it is inconvenient or impractical to obtain a population sample, but it is practical to obtain a convenience sample of units with different X values, such that within the X = 0 and X = 1 subsamples the Y values are representative of the population (i.e. they follow the correct conditional probabilities).
- Suppose the marginal distribution of one variable, say X, is very skewed. For example, if we are studying the relationship between high alcohol consumption and pancreatic cancer in the general population, the incidence of pancreatic cancer would be very low, so it would require a very large population sample to get a modest number of pancreatic cancer cases. However we could use data from hospitals to contact most or all of their pancreatic cancer patients, and then randomly sample an equal number of subjects without pancreatic cancer (this is called a "case-control study").
In both these settings, the odds ratio can be calculated from the selected sample, without biasing the results relative to what would have been obtained for a population sample.
Use in quantitative research
Due to the widespread use of logistic regression, the odds ratio is widely used in many fields of medical and social science research. The odds ratio is commonly used in survey research, in epidemiology, and to express the results of some clinical trials, such as in case-control studies. It is often abbreviated "OR" in reports. When data from multiple surveys is combined, it will often be expressed as "pooled OR".
Relation to relative risk
In clinical studies, as well as in some other settings, the parameter of greatest interest is often the relative risk rather than the odds ratio. The relative risk is best estimated using a population sample, but if the rare disease assumption holds, the odds ratio is a good approximation to the relative risk — the odds is p / (1 − p), so when p moves towards zero, 1 − p moves towards 1, meaning that the odds approaches the risk, and the odds ratio approaches the relative risk.[5] When the rare disease assumption does not hold, the odds ratio can overestimate the relative risk.[6][7][8]
If the absolute risk in the control group is available, conversion between the two is calculated by:[6]:
where:
- RR = relative risk
- OR = odds ratio
- RC = absolute risk in the unexposed group, given as a fraction (for example: fill in 10% risk as 0.1)
Invertible Property and Invariance of the Odds Ratio
The odds ratio has another unique property of being directly mathematically invertible whether analyzing the OR as either disease survival or disease onset incidence - where the OR for survival is direct reciprocal of 1/OR for risk. This is known as the 'invariance of the odds ratio'. In contrast, the relative risk does not possess this mathematical invertible property when studying disease survival vs. onset incidence. This phenomenon of OR invertibility vs. RR non-invertibility is best illustrated with an example:
Suppose in a clinical trial, one has an adverse event risk of 4/100 in drug group, and 2/100 in placebo... yielding a RR=2 and OR=2.04166 for drug-vs-placebo adverse risk. However, if analysis was inverted and adverse events were instead analyzed as event-free survival, then the drug group would have a rate of 96/100, and placebo group would have a rate of 98/100—yielding a drug-vs-placebo a RR=0.9796 for survival, but an OR=0.48979. As one can see, a RR of 0.9796 is clearly not the reciprocal of a RR of 2. In contrast, an OR of 0.48979 is indeed the direct reciprocal of an OR of 2.04166.
This is again what is called the 'invariance of the odds ratio', and why a RR for survival is not the same as a RR for risk, while the OR has this symmetrical property when analyzing either survival or adverse risk. The danger to clinical interpretation for the OR comes when the adverse event rate is not rare, thereby over-exaggerating differences when the OR rare-disease assumption is not met. On the other hand, when the disease is rare, using a RR for survival (e.g. the RR=0.9796 from above example) can clinically hide and conceal an important doubling of adverse risk associated with a drug or exposure.
Alternative estimators of the odds ratio
The sample odds ratio n11n00 / n10n01 is easy to calculate, and for moderate and large samples performs well as an estimator of the population odds ratio. When one or more of the cells in the contingency table can have a small value, the sample odds ratio can be biased and exhibit high variance. A number of alternative estimators of the odds ratio have been proposed to address this issue. One alternative estimator is the conditional maximum likelihood estimator, which conditions on the row and column margins when forming the likelihood to maximize (as in Fisher's exact test).[9] Another alternative estimator is the Mantel-Haenszel estimator.
Numerical examples
The following four contingency tables contain observed cell counts, along with the corresponding sample odds ratio (OR) and sample log odds ratio (LOR):
OR = 1, LOR = 0 OR = 1, LOR = 0 OR = 4, LOR = 1.39 OR = 0.25, LOR = −1.39 Y = 1 Y = 0 Y = 1 Y = 0 Y = 1 Y = 0 Y = 1 Y = 0 X = 1 10 10 100 100 20 10 10 20 X = 0 5 5 50 50 10 20 20 10 The following joint probability distributions contain the population cell probabilities, along with the corresponding population odds ratio (OR) and population log odds ratio (LOR):
OR = 1, LOR = 0 OR = 1, LOR = 0 OR = 16, LOR = 2.77 OR = 0.67, LOR = −0.41 Y = 1 Y = 0 Y = 1 Y = 0 Y = 1 Y = 0 Y = 1 Y = 0 X = 1 0.2 0.2 0.4 0.4 0.4 0.1 0.1 0.3 X = 0 0.3 0.3 0.1 0.1 0.1 0.4 0.2 0.4 Worked example
Example 1: risk reduction Example 2: risk increase Experimental group (E) Control group (C) Total (E) (C) Events (E) EE = 15 CE = 100 115 EE = 75 CE = 100 Non-events (N) EN = 135 CN = 150 285 EN = 75 CN = 150 Total subjects (S) ES = EE + EN = 150 CS = CE + CN = 250 400 ES = 150 CS = 250 Event rate (ER) EER = EE / ES = 0.1, or 10% CER = CE / CS = 0.4, or 40% N/A EER = 0.5 (50%) CER = 0.4 (40%) Equation Variable Abbr. Example 1 Example 2 CER − EER < 0: absolute risk reduction ARR (−)0.3, or (−)30% N/A > 0: absolute risk increase ARI N/A 0.1, or 10% (CER − EER) / CER < 0: relative risk reduction RRR (−)0.75, or (−)75% N/A > 0: relative risk increase RRI N/A 0.25, or 25% 1 / (CER − EER) < 0: number needed to treat NNT (−)3.33 N/A > 0: number needed to harm NNH N/A 10 EER / CER relative risk RR 0.25 1.25 (EE / EN) / (CE / CN) odds ratio OR 0.167 1.5 EER − CER attributable risk AR (−)0.30, or (−)30% 0.1, or 10% (RR − 1) / RR attributable risk percent ARP N/A 20% 1 − RR (or 1 − OR) preventive fraction PF 0.75, or 75% N/A See also
External links
- Odds Ratio Calculator — website
- Odds ratio definition and examples
- OpenEpi, a web-based program that calculates the odds ratio, both unmatched and pair-matched
References
- ^ Cornfield, J. "A Method for Estimating Comparative Rates from Clinical Data. Applications to Cancer of the Lung, Breast, and Cervix". Journal of the National Cancer Institute 11: 1269–1275.
- ^ Mosteller, Frederick (1968). "Association and Estimation in Contingency Tables". Journal of the American Statistical Association (American Statistical Association) 63 (321): 1–28. doi:10.2307/2283825. JSTOR 2283825.
- ^ Edwards, A.W.F. (1963). "The measure of association in a 2x2 table". Journal of the Royal Statistical Society, Series A (Blackwell Publishing) 126 (1): 109–114. doi:10.2307/2982448. JSTOR 2982448.
- ^ Morris and Gardner; Gardner, MJ (1988). "Calculating confidence intervals for relative risks (odds ratios) and standardised ratios and rates". British Medical Journal 296 (6632): 1313–1316. doi:10.1136/bmj.296.6632.1313. PMC 2545775. PMID 3133061. http://www.bmj.com/cgi/reprint/296/6632/1313.
- ^ Viera AJ (July 2008). "Odds ratios and risk ratios: what's the difference and why does it matter?". South. Med. J. 101 (7): 730–4. doi:10.1097/SMJ.0b013e31817a7ee4. PMID 18580722. http://meta.wkhealth.com/pt/pt-core/template-journal/lwwgateway/media/landingpage.htm?issn=0038-4348&volume=101&issue=7&spage=730.
- ^ a b Zhang J, Yu KF (November 1998). "What's the relative risk? A method of correcting the odds ratio in cohort studies of common outcomes". JAMA 280 (19): 1690–1. doi:10.1001/jama.280.19.1690. PMID 9832001. http://jama.ama-assn.org/cgi/pmidlookup?view=long&pmid=9832001.
- ^ Robbins AS, Chao SY, Fonseca VP (October 2002). "What's the relative risk? A method to directly estimate risk ratios in cohort studies of common outcomes". Ann Epidemiol 12 (7): 452–4. doi:10.1016/S1047-2797(01)00278-2. PMID 12377421. http://linkinghub.elsevier.com/retrieve/pii/S1047279701002782.
- ^ Nurminen, Markku (1995). "To Use or Not to Use the Odds Ratio in Epidemiologic Analyses?". European Journal of Epidemiology 11 (4): 365–371. doi:10.1007/BF01721219. JSTOR 3582428.
- ^ Rothman, Kenneth J.; Greenland, Sander; Lash, Timothy L. (2008). Modern Epidemiology. Lippincott Williams & Wilkins. ISBN 0781755646.
Biomedical research: Clinical study design / Design of experiments Overview Controlled study
(EBM I to II-1; A to B)Observational study
(EBM II-2 to II-3; B to C)Epidemiology/
methodsoccurrence: Incidence (Cumulative incidence) · Prevalence (Point prevalence, Period prevalence)
association: absolute (Absolute risk reduction, Attributable risk, Attributable risk percent) · relative (Relative risk, Odds ratio, Hazard ratio)
other: Virulence · Infectivity · Mortality rate · Morbidity · Case fatality · Specificity and sensitivity · Likelihood-ratios · Pre/post-test probabilityTrial/test types Analysis of clinical trials Risk–benefit analysis
Interpretation of results Categories:- Epidemiology
- Medical statistics
- Statistical terminology
- Bayesian statistics
Wikimedia Foundation. 2010.









