Dirac comb

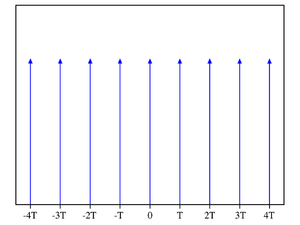A Dirac comb is an infinite series of Dirac delta functions spaced at intervals of T

In mathematics, a Dirac comb (also known as an impulse train and sampling function in electrical engineering) is a periodic Schwartz distribution constructed from Dirac delta functions

$\Delta_T(t) \ \stackrel{\mathrm{def}}{=}\ \sum_{k=-\infty}^{\infty} \delta(t - k T)$

for some given period T. Some authors, notably Bracewell as well as some textbook authors in electrical engineering and circuit theory, refer to it as the Shah function (possibly because its graph resembles the shape of the Cyrillic letter sha Ш). Because the Dirac comb function is periodic, it can be represented as a Fourier series:

$\Delta_T(t) = \frac{1}{T}\sum_{n=-\infty}^{\infty} e^{i 2 \pi n t/T}.$

Scaling property

The scaling property follows directly from the properties of the Dirac delta function

$\sum_{k=-\infty}^{\infty} \delta(t - k T) = |\alpha|\cdot \sum_{k=-\infty}^{\infty} \delta\bigg(\alpha\cdot (t - k T)\bigg).$

Fourier series

It is clear that Δ_T(t) is periodic with period T. That is

$\Delta_T(t+T) = \Delta_T(t)\,$

for all t. The complex Fourier series for such a periodic function is

$\Delta_T(t) = \sum_{n=-\infty}^{+\infty} c_n e^{i 2 \pi n t/T} \$

where the Fourier coefficients, c_n are

$c_n\,$	$= \frac{1}{T} \int_{t_0}^{t_0 + T} \Delta_T(t) e^{-i 2 \pi n t/T}\, dt \quad ( -\infty < t_0 < +\infty ) \$
	$= \frac{1}{T} \int_{-T/2}^{T/2} \Delta_T(t) e^{-i 2 \pi n t/T}\, dt \$
	$= \frac{1}{T} \int_{-T/2}^{T/2} \delta(t) e^{-i 2 \pi n t/T}\, dt \$
	$= \frac{1}{T} e^{-i 2 \pi n \, 0/T} \$
	$= \frac{1}{T}. \$

All Fourier coefficients are 1/T resulting in

$\Delta_T(t) = \frac{1}{T}\sum_{n=-\infty}^{\infty} e^{i 2 \pi n t/T}.$

Fourier transform

The Fourier transform of a Dirac comb is also a Dirac comb.

Unitary transform to ordinary frequency domain (Hz):

$\sum_{n=-\infty}^{\infty} \delta(t - n T) \quad \stackrel{\mathcal{F}}{\longleftrightarrow}\quad {1\over T}\sum_{k=-\infty}^{\infty} \delta \left( f - {k\over T} \right) \quad = \sum_{n=-\infty}^{\infty} e^{-i2\pi fnT}.$

Unitary transform to angular frequency domain (radian/s):

$\sum_{n=-\infty}^{\infty} \delta (t - n T) \quad \stackrel{\mathcal{F}}{\longleftrightarrow}\quad \frac{\sqrt{2\pi }}{T} \sum_{k=-\infty}^{\infty} \delta \left( \omega -k \frac{2\pi }{T}\right) \quad = \frac{1}{\sqrt{2\pi}}\sum_{n=-\infty}^{\infty} e^{-i\omega nT}. \,$

Sampling and aliasing

Main article: Nyquist–Shannon sampling theorem

Reconstruction of a continuous signal from samples taken at sampling interval T is done by some sort of interpolation, such as the Whittaker–Shannon interpolation formula. Mathematically, that process is often modelled as the output of a lowpass filter whose input is a Dirac comb whose teeth have been weighted by the sample values. Such a comb is equivalent to the product of a comb and the original continuous signal. That mathematical abstraction is often described as "sampling" for purposes of introducing the subjects of aliasing and the Nyquist-Shannon sampling theorem.

Use in directional statistics

In directional statistics, the Dirac comb of period 2π is equivalent to a wrapped Dirac delta function, and is the analog of the Dirac delta function in linear statistics.

In linear statistics, the random variable (x) is usually distributed over the real number line, or some subset thereof, and the probability density of x is a function whose domain is the set real numbers, and whose integral from $-\infty$ to $+\infty$ is unity. In directional statistics, the random variable (θ) is distributed over the unit circle and the probability density of θ is a function whose domain is some interval of the real numbers of length 2π and whose integral over that interval is unity. Just as the integral of the product of a Dirac delta function with an arbitrary function over the real number line yields the value of that function at zero, so the integral of the product of a Dirac comb of period 2π with an arbitrary function of period 2π over the unit circle yields the value of that function at zero.

See also

• Frequency comb
• Poisson summation formula

References

• Bracewell, R.N. (1986), The Fourier Transform and Its Applications (revised ed.), McGraw-Hill ; 1st ed. 1965, 2nd ed. 1978.
• Córdoba, A (1989), "Dirac combs", Letters in Mathematical Physics 17 (3): 191–196, doi:10.1007/BF00401584