Mathematics of radio engineering

A complex-valued function.

The mathematics of radio engineering is a pleasant and very useful subject. This article is an attempt to provide a reasonably comprehensive summary of this almost limitless topic. While the ideas have historically taken some getting used to, one of the goals here is to present them in a more readable way than is normally found in rigorous texts. Almost the entire subject is based on complex analysis, which has a reputation for being rather beautiful. Also, it is a relief to most people when they hear that this does not necessarily mean "complicated". In fact, some of the old names for the complex plane are still occasionally used today, such as the Gauss plane and the Argand plane.

This article covers the subject from the early days of radio, all the way to modern high-speed integrated systems. It begins very simply, and becomes a little more involved later on. But not everything can be stated in everyday terms. Perhaps one or two years of university-level math are required to understand it, although there are extensive footnotes for the reader who may not have had the time for extensive preparation.

The article focuses more on the mathematical aspects, and does not cover the history in depth. For a more detailed historical account, timeline of electromagnetic theory is recommended.

The superposition principle

People have studied waves since ancient times. As time has passed, they have developed many different techniques for studying them. Perhaps the most useful idea is the superposition principle. It means that waves just add; in this one case, there are no complicated formulas. It applies to almost all waves, except ocean waves, because ocean waves break. However it still applies to them if they are not too strong. The concept appears in myriad different ways, and is used throughout the article.

One of the earlier theories that made use of it was Huygen's principle, which said that each wavefront creates an infinite number of new wavefronts, and so on ad infinitum. As the wavefronts overlap each other, they can be added to produce the correct results.

The development of "wireless"

Spark-gap transmitters and lightning

The existence of electromagnetic waves was first proven by Heinrich Hertz in 1887. After this, there were many public exhibitions of the effect, generally employing very primitive sending and receiving devices. As time went on, experimenters began developing their own devices, and the practice of radio took off.

In these early days, people often used spark gaps. These generate very small bolts of lightning. Lightning works as follows: when the voltage difference is strong enough between the sky and the earth, the atmosphere breaks down, and current is able to flow. So they put a large voltage between two pieces of metal, and the same thing happened.

The problem was that lightning is not tuned to a single frequency. A spike of that intensity in the time domain is a delta function. If one were to Fourier transform it, and graph it in the frequency domain, it would almost cover almost the entire spectrum.

Therefore radio hobbyists were constantly "stepping on" each other, and there was a lot of interference. Moreover the efficiency was very low: 99% of the energy went into heat and light, and only one percent went into communications. But things were soon to improve.

AM communications

The first AC generators were not as efficient as the ones in cell phones.

As people experimented with various ideas, they began to realize that they could transmit on only one frequency at a time; or at least they could reduce the bandwidth so that it would approximate a single frequency. Then they would vary the height^{[note 1]} of the wave to make signals. This became known as AM radio. However it was still somewhat inefficient, because it involved the multiplication of signals, and that generates sidebands. These are also called sum and difference frequencies. So they sent the information, the sidebands, and anything else that accidentally happened to get transmitted. The next step was to send only one sideband, and to block everything else. This was much more efficient. Many other developments followed soon afterward.

Where the sidebands come from

The sum and difference frequencies show the value of complex numbers. They exist because the most general expression for a cosine wave is really

$\,\cos(z) = \frac{e^{-i z} + e^{i z}}{2}$

where one has both positive and negative frequency components. These occur because a cosine wave is the solution of a linear differential equation, and therefore it obeys the superposition principle: the sum of two solutions is again a solution. This is a famous result from the theory of differential equations. These mirror images will not show up on a spectrum analyzer, unless it is designed to display them.

The negative frequencies are sometimes thought of as unimportant, but the truth is that the sidebands would not exist without them. So when one multiplies two cosine waves, one finds that

$\,\cos(\omega z)\cos(\phi z) = [\frac{e^{-i\omega z} + e^{i\omega z}}{2}][\frac{e^{-i\phi z} + e^{i\phi z}}{2}]$

$\,= \frac{ \overbrace{ e^{-i[\omega - \phi] z}+e^{-i[\omega + \phi] z}}^{negative.frequencies}+\overbrace{e^{i[\omega - \phi] z}+e^{i[\omega + \phi] z}}^{positive.frequencies}}{4}$

The two on the right are the sum and difference, while the two on the left are the negative of those. Note that in the general case omega and phi can be any two dimensionless complex numbers, so that the sum and difference may not necessarily lie on the imaginary axis.

The popularity of amateur radio

Homebrew enthusiasts now have the option of using this arbitrary waveform generator.

It was not long before people began licensing radio hobbyists. This was called amateur radio, or ham radio. Hobbyists became known as "hams". Most of the major breakthroughs in radio theory were made by hams.

One difficulty was that there were no crystal oscillators in those days, so they had to design their own frequency generators. Someone might ask "how fast is your computer?", and the person might answer, "two gigahertz". In contrast, these generators were very slow. For instance, if someone were transmitting on 25 kHz, that would be 0.000025 gigahertz. To get an antenna to resonate at that speed, one first divides the speed of light by the frequency, in order to get the wavelength. Therefore, a standard half-wavelength antenna would have to be 3.7 miles long. This was considered impractical, especially if one lived in an apartment building.

Ham radio was still strong throughout the 70s and 80s. However, with the rise of cell phones and the internet, the venerable hobby has experienced a challenge that it may not recover from. While there are still contests and group projects and so on, the number of members is now quite low by comparison. Yet it still remains one of the best ways to begin learning the subject, and will always be a part of radio lore.

Filters

RLC filters

These are the easiest type of filters to make. The R stands for resistor, the L for inductor, and the C for capacitor. One constructs a loop of copper wire, and connects it to a battery. The elements are placed at different locations in the loop. Mathematically, each loop is a map of the complex plane that simply moves the pole and the zero.^{[note 2]} The function can signify either impedance or admittance. If one takes the reciprocal, the poles and zeros just switch places.

If one connects a number of these loops together, then one simply gets more poles and zeros moved around. Therefore one could suppose there is an infinite stack of complex planes; each new current loop takes a pancake off the stack, and moves the poles and zeros around.

One may also start with an infinite number of separate one-loop circuits. One may think of each loop as a potential well, and the current flow as a particle of sorts. Since the loops are not connected, none of the particles know about each other. There is infinite impedance between the current loops. Now if one lowers the impedance between them, then they are affected a little; and if one lowers the impedance even more, then they affected even more. At this point the potential well becomes a complicated surface with many particles bumping into each other.

One may also imagine these starting conditions as a matrix of frequencies. If the matrix is diagonal, then the terms do not affect each other: the sum and product of diagonal matrices is diagonal. But if one introduces off-diagonal elements, then there is an interaction between the terms, and the sum and product of the matrices is more complicated. If one was to assume that the infinite list of frequencies were gradually increasing, and that none were left out, then this would also a way of representating the frequency domain. One could have an oscilloscope that makes graphs with an off-diagonal version of the domain just like this one, and it would still be correct - as long as one did the computations carefully.

One way of adding off-diagonal elements to the admittance matrix x is to multiply it by a non-diagonal matrix a in the following way:

$x \to a^{-n}xa^{n}$

At first this mapping may seems strange, but it has the useful property that the determinant is the same:

$\,\det(a^{-n}xa^{n}) = \det(a^{-n})\det(x)\det(a^n)$

$\, = \det(a^{-n})\det(a^n)\det(x)$

$\, = \det(x)$

This leads to many interesting results. For instance, if n is close to zero, then it represents a small connection between the current loops; the larger it is, the more of a connection there is. This allows a smooth transition from non-interaction to interacting.

Linear vs non-linear filters

All of the above filters are linear. This means that the superposition law holds, or that a generalized version of Ohms law is obeyed. It is often stated as V = IR, where all three are complex matrices.^{[note 3]} And if there is a bias voltage S, then it can be written as V = S + IR, where S and R are constants. One may interpret this as the first two terms of a taylor series:

$\,V = \overbrace{S}^{1} + \overbrace{IR}^{x*3}$

where 1 + 3x is simply used as an example of a linear function. Now the series may be continued as

$\,1 + 3x + 2x^2 - 4x^3 + \cdots$

and one has a nonlinear circuit. It is actually true all the time, but the extra terms are usually so small that they are not noticed. The easiest way to generate them is to use a "one-way component" commonly known as a diode. It simply lets the current flow one way and not the other.

Quartz, mechanical and MEMS devices

One of the problems that comes along with these filters is that they don't work very well at higher frequencies. Therefore one wants to design filters that have a higher quality factor at these frequencies, and this calls for improved technology. The first step in this direction was to notice that crystals behave like a tuning fork, and that they also have very high quality factors. So one feeds the current through a crystal, and it is tuned much better. Another step was the use of mechanical oscillators, which are also very interesting. These are thoroughly described in the featured article on mechanical filters. Today, the design fabrication process has improved to the point where the dimensions of the objects are surprisingly small, and so the quality factor and the frequencies are much higher. These are known as MEMS devices.

Maxwell's equations

A simpler expression for free waves

Free waves are those that are travelling through the atmosphere, or through empty space; they are not connected with charged particles or currents. These are the types of waves that are transmitted from an antenna, or from a computer. In this case, it is possible to achieve a simplification of the theory. In the absence of charges and currents, Maxwell's equations become^[1]

$\nabla \cdot (E + iB) = 0$

$\nabla \times (E + iB) = i\frac{\partial}{\partial t}(E+iB)$

Here one has introduced a complex-valued field E+iB.^[2] In this way of thinking, one finds that there is a new symmetry given by

$E + iB \rightarrow e^{i\theta}(E + iB)$

This is a simplification of the theory. The fields are simply rotating, and the frequency is much easier to see. If one were able to plot graphs in three dimensions, one could even use these as a basis for the frequency domain. This is because only the real portion of the waves appear in reality.

Maxwell's equations with quaternions

Maxwell's equations are especially well adapted for the quaternions. One reason is that they stay the same when the reference frame is moving. When Lorentz discovered this in the 1870s, he was very surprised, and thought it might be some kind of unimportant curiosity. As time went on however, people found that these Lorentz transformations were more important than they had thought.

This idea involves quaternions with complex coefficients, sometimes called biquaternions. One defines a four vector as follows:

$\,q = ia + b\mathbf{i}+ c\mathbf{j}+ d\mathbf{k}$

where a, b, c and d are real numbers. Then the length of q is

$\,q\overline{q} = -a^2 + b^2+ c^2 +d^2$

which is nice because it is the minkowski metric. The Lorentz transform of a biquaternion q has a surprisingly simple form:

$\,e^{+{1\over 2} n\theta}q {e^{-{1\over 2} n\theta}}^{*}$

$\,e^{+{1\over 2}i n\theta}q {e^{-{1\over 2}i n\theta}}^{*}$

The first is a rotation by an angle θ around an 3-vector n; the second is a boost by a hyperbolic angle θ in the direction of n. The vector n can be thought of as an element of SU(2), because it has length one, and can point in any of three directions. The star means complex conjugation of the first term. Very similar formulas can be found in the article on quaternions and spatial rotations, which covers this from a purely mathematical viewpoint but does not cover electromagnetism.^{[note 4]}

Now that invariance under Lorentz transformations has been established,^{[note 5]} all that is left to do is write the equations in biquaternionic form, and one finds that they reduce to a single equation:^[3]

$D\overline{D}A = -J$

where

$\,A = i\phi + A_1\mathbf{i}+ A_2\mathbf{j}+ A_3\mathbf{k}\quad$ - four-potential

$\,J = i\rho+ J_1\mathbf{i}+ J_2\mathbf{j}+ J_3\mathbf{k}\quad$ - four-current

$\,\overline{D} = i{\partial/\partial t} + {\partial/\partial x}\mathbf{i}+{\partial/\partial y}\mathbf{j}+ {\partial/\partial z}\mathbf{k} \quad$ - covariant four-derivative

$\,D = i{\partial/\partial t} - {\partial/\partial x}\mathbf{i}-{\partial/\partial y}\mathbf{j}- {\partial/\partial z}\mathbf{k} \quad$ - contravariant four-derivative

The $D \overline{D}$ term is interesting. Since each factor D is four-dimensional, the product should be 16-dimensional. Yet the terms intricately cancel, and there are only four left. This is the D'alambert operator, viz

$\,D\overline{D} = -{\partial^2/\partial t^2} + {\partial^2/\partial x^2 }+{\partial^2/\partial y^2 }+{\partial^2/\partial z^2} \quad$

The reason this is true

This is really an example of Noether's theorem, which says if there is a symmetry in a certain theory, then there will also be a conservation law in that theory. In this case the symmetry is the Lorentz group, and what is conserved is Maxwell's equations. The E and B fields become different, but the equations they form do not.

Electromagnetism has been studied from a vast array of viewpoints. The goal is to understand the deeper reasons for it. The most successful generalization is the electroweak theory. More speculative ideas are the SU(5) and SO(10) theories. Some theories are unusually speculative. For instance, if one applies the Cayley-Dickson construction to the quaternions three times over, one arrives at the 32-dimensional "trigintaduonions", in which "it is believed that electromagnetic-gravitational field, strong-weak field, hyper-strong field and hyper-weak field are unified, equal and interconnected."^[4] The next section provides an interesting generalization based on the possible existence of both electric and magnetic charge.

A symmetric version of the equations

One notices that electric charge has radial "lines of force" emanating from it. In addition, magnetic poles have concentric "circles of force" radiating from them. One could make a two-dimensional version of this by means of the complex plane. The lines of force are of the form

$\,e^{ki + j}$

where k is a constant, and j ranges over all real numbers. For instance, if k is zero, then e^j is a line of force that goes from zero to infinity. On the other hand, the circles of force are of the form

$\,e^{k + ij}$

where k is a constant, and ij ranges over all imaginary numbers. For instance, if k is zero, then e^ij is the unit circle. One switches from one to the other by multiplying the exponents by i. Therefore one might associate electricity with real numbers, and magnetism with imaginary numbers. Since this is only a two-dimensional version of the idea, one would like to rework this into something that is consistent with four-dimensional spacetime, and with the transformations of special relativity.

Many ideas of this kind have led to the concept of dyons.^[5][6] These are hypothetical particles with both electric and magnetic charge; blending them into one allows them to generate one united field. One writes them like this:

$\,e + ig$

where e is the electric charge and g is the magnetic charge. In the previous section, it was shown how Maxwell's equations can be expressed with quaternions. Yet these equations do not include magnetic charge, because it still has not been experimentally observed. The reader may wonder why such ghostly things as magnetic charge should be studied at all. The answer is that it can simplify the equations dramatically, just as complex numbers simplify circuit equations. Also the majority of macroscopic phenomena would be the same if they existed. Finally, they may well exist, but for some unknown reason have not quite been observed yet, despite many searches for them. So in this spirit of adventure, one group of researchers introduce the magnetic counterpart of the quaternionic A and J vectors as follows:^{[7][note 6]}

$\,B = i\phi_2 + B_1\mathbf{i}+ B_2\mathbf{j}+ B_3\mathbf{k}\qquad$ - magnetic four-potential

$\,K = i\rho_2 + K_1\mathbf{i}+ K_2\mathbf{j}+ K_3\mathbf{k}\qquad$ - magnetic four-current

The complete complex quaternionic fields are therefore

$\,A+iB = [i\phi_1-\phi_2] + [A_1 +iB_1]\mathbf{i}+ [A_2+iB_2]\mathbf{j}+ [A_3+iB_3]\mathbf{k}\quad$

$\,J+iK = [i\rho_1-\rho_2]+ [J_1+iK_1]\mathbf{i}+ [J_2+iK_2]\mathbf{j}+ [J_3+iK_3]\mathbf{k}\quad$

The important point is that the two biquaternionic fields match perfectly, because

the i is switched in the magnetic quaternions

One may also introduce a magnetic electromagnetic tensor, usually denoted by F^uv, but in this case by iF^uv. Moreover we have the following symmetries

$\,\{e+ig\} = e^{i\theta}\{e+ig\}$

$\,\{A+iB\} = e^{i\theta}\{A+iB\}$

$\,\{J+iK\} = e^{i\theta}\{J+iK\}$

$\,\{F^{uv}+iF^{uv}\} = e^{i\theta}\{F^{uv}+iF^{uv}\}$

The researchers^[7] go on to derive the complete symmetric equations from these, as well as several other results. It might also be noted that in this way of thinking, there is no divergence, gradient, curl, or vector calculus. Instead, there is only two-by-two matrix multiplication. This is because the complete biquaternion algebra is the same as the algebra of two-by-two complex matrices (in eight dimensions). This makes the subject much easier to work with.

A breakthrough: path integrals

Introduction

While Maxwell's equation were immensely successful in predicting electromagnetic phenomena for most applications, there was still a feeling that they were somehow lacking. Radio theory should be seamlessly blended with the new molecular chemistry and medicine that were developing at that time, and yet it was not. The answer to this dilemma was provided by the theory of path integrals. They simplified and unified many branches of science in a new and unique way.

The idea was that the light waves are replaced by a diffusion process that uses complex numbers. In this way of thinking, there are only interference patterns,^{[note 7]} similar to how antenna patterns are formed from interference:

	pattern	caused by
microscopic	particle probability patterns	interference from lots of particle waves
macroscopic	antenna energy patterns	interference from lots of antennas

Moreover the field strength was replaced by probability functions. So the waves were still there in the macroscopic realms, but now they were caused by infinitesimal particles.

Antenna patterns

The S-Meter on a radio transceiver.

There is a small handheld device known as a field strength meter. One stands in front of the antenna (not recommended when transmitting), and measures the field strength. As one moves around, one gets a feel for the antenna radiation pattern. In theory, one could make a very accurate picture of the antenna pattern with this method, depending on how much time one spends on it. But in the quantum way of thinking, one is really constructing a probability function instead. The same is true for a cell phone. Instead of thinking of the five bars as a field strength, one may interpret them as a probability function; or more accurately, as a probability histogram.

Path integrals as a determinant

A random walk in two dimensions.

Path integrals can be expressed as structures that are related to the determinant of a matrix. For bosons, one computes the permanent; for fermions, the determinant; for anyons, the immanant. They can be thought of as sums of random walks in different arithmetic systems. As the number of random zig-zags approaches infinity, the matrix becomes infinite dimensional.

It has been mentioned how the superposition principle applies to light and radio waves (that is, bosons). This is why the permanent is used for light and radio waves: complex numbers are added together and they produce interference patterns: these are of the form xy + yx. But a different kind of superposition principle applies to electrons (that is, fermions). Instead of getting stronger when they are the same, they get weaker. And instead of getting weaker when they are different, they get stronger. So in contrast to the case of radio waves, the determinant is used for electrons and other similar particles. Complex "numbers" are added together to produce interference patterns: these are of the form xy - yx. These are difficult to get used to. Anyons are even more unusual, so this article will not go into them in any more detail.

Complex functions

The science of poles and zeros

A soap bubble forms a minimal surface.

Complex functions are different from real functions. They are uniquely determined by the poles and zeros.^{[note 8]} One might imagine a soap bubble that finds a minimal surface of the poles and zeros. If the poles and zeros transform, the soap bubble moves; if they don't, it stays the same.

One of the surprising features is that they can exist at infinity as well. For instance, if there is no distortion at all, the function is zero at zero, and infinity at infinity. This is so obvious that it may be confusing. However it shows an important point: even the plane itself is determined by the poles and zeros. Therefore they always exist in pairs. Even if there doesn't seem to be an equal number of them, the extra ones are still there.

A complex function with poles in the left half of the s-plane.

Another important point is that poles and zeros can be approached from every direction at once. If one moves toward the positive x axis, or the negative x axis, or the positive y axis, or in any direction at all, and keeps going forever, one will arrive at the same point: the point at infinity.

Complex functions also have a dual nature, just as time and frequency response graphs do. In this case, it is the Laplace transform and its inverse that map one to the other. It seems remarkable that the transform can process that much detailed information, and still leave all of the structure the same.

One of the many uses for these functions is as impedance or admittance functions in the analysis of linear systems. This is valuable because every system can be made linear, by looking at smaller and smaller portions of it in the time-frequency domain. Moreover, if one uses several of them to form the basis of a vector space, the system can be n-dimensional.

Useful theorems

There is a long list of useful ideas in complex analysis, going from the reasonably clear to the those that are more difficult. Here are several of the best (and easiest) ones. These theorems are stated unusually simply, a bit like crib notes, in order to bring out the meaning.^{[note 9]}

• Holomorphic function - A function which is differentiable from every complex direction at once.^{[note 10]}
• Entire function - A function which is differentiable for every possible complex input.
• Meromorphic function - Has only a countable number of isolated poles.
• Liouville's theorem - Unless the entire plane is mapped to a single point, an entire function is unbounded.
• Picard's little theorem - An entire function outputs every possible complex number, except perhaps one complex number.
• Schwarz-Christoffel transformation - Maps the upper half plane to polygons; again, soap bubbles are important here.
• Identity theorem - If a differentiable function f = g on one part of a domain, the f = g over the whole domain.
• Riemann mapping theorem - any simply connected domain of the complex plane can be mapped conformally to the unit disk.
• Residue theorem - The integral of a differentiable function is 2πi times the sum of the residues.
• Argument principle - If f is meromorphic then the integral of its logarithmic derivative is 2πi times the number of zeros minus the number of poles.
• Cauchy integral formula - A method of computing derivatives by computing integrals.

Reversible computing

If one includes the point at infinity, the complex plane becomes a compact space,^{[note 11]} and the set of all conformal transformations becomes the mobius group. Each of these moves the pole and the zero around.^{[note 12]} Therefore each is equivalent to a one-loop RLC filter, and the set of one-loop filters is a group as well. However, at least half of these filters are not physically realizable, because the pole is in the right half of the s-plane.

If one starts with an LC filter, adding a positive resistance would cause the oscillations to fade out. One notices that a negative resistance would cause the oscillations to increase. From a mathematical point of view, this is perfectly reasonable. In terms of the Riemann sphere, the former causes the oscillations to converge asymptotically to zero, while the latter causes them to converge asymptotically to infinity, and they are just the mirror-image of each other. The unusual feedback circuits do not emit and dissipate energy, but instead absorb and organize energy. Instead of heating up, a laptop computer would get colder and colder, and could actually serve as a refrigerator.

The central idea here is that of reversibility. One is really allowing time to run backwards, and this is why the computer cools off and creates "reverse entropy". And this is indeed the focus of much current research. Systems of this type are called reversible systems, and they are the heart and soul of quantum computation. Therefore, the concept of conformal transformations is itself transformed, and one arrives at the concept of a unitary transformation of a Hilbert space.

An important point here is that from a topological point of view, all of these filters are identical.^{[note 13]} Therefore one may employ big words: every one-loop filter is a diffeomorphism of every other one. This also carries over to higher-order filters: if there are two filters with the same number of poles and zeros, then they are topologically identical, and therefore homeomorphic.

Integral transforms

When astronomers are looking at the sky, they often adjust the telescope in order to refine the results. In the same way, some math problems are easier to solve when they are transformed. This is the idea behind integral transforms: one just rotates the problem to make it simpler.

Linear transformations

As mentioned before, the first two terms of a taylor series are very simple, as follows:

$\,1 + 3x$

This means that the variable x is multiplied by a factor of three, and the entire thing is moved over by one. If one concentrates solely on the second term, this gives rise to the entire field of group theory. Finite groups are collections of invertible matrices^{[note 14]} that are applied to a variable.^{[note 15]} All of the other coefficients can be matrices as well. In this case, the 3 is a one dimensional matrix in the group of positive real numbers.

The 1 on the other hand, just slides the group over. It is not classified as a linear transformation, but is instead known as an affine transformation. As more terms appear in the power series, things become nonlinear, and the theory becomes more involved. However in summary, a linear transformation can just be thought of as a matrix.

Fourier, Laplace, Z, Bessel, etc.

All of the integral transforms can be expressed as linear transformations; that is, as matrices.^{[note 16]} They simply have a different basis. The Fourier transform sends things to one basis, and the Bessel transform to another. One chooses the most convenient basis for studying the problem.

The most important one is the Fourier transform. The entire industry is built on this one idea. Spectrum analyzers and oscilloscopes routinely switch back and forth between different displays by means of the Fourier transform. The next most important is the Laplace transform. It provides useful information on stability and causality of linear systems. Also, one can compute the output just by multiplying the impulse response by the input function. After that there are about twenty or thirty others, and new ones all the time.

One notices that every frequency band of the spectrum can be written as a collection of individual frequencies; that is, complex-valued functions. Therefore, the full spectrum becomes a continuous vector space of functions, sometimes called a topological vector space. The set of subsets forms a lattice (and is also a Boolean algebra in the finite dimensional case). Another way of saying this is that each subspace each is a direct sum^{[note 17]} of basis vectors. This allows one to gain more insight into the nature of these integral transforms.

The continuous integral transforms are not really separate from each other. By changing the basis functions infinitesimally, one moves to a different transform. Therefore each can be rotated into the others.

There are also four-dimensional versions of the transforms, which allow special relativity to play a role. Instead of a basis of functions like

$\,e^{i\omega t}$

one might replace them with

$\,e^{i\Omega[\sqrt{t^2-x^2-y^2-z^2}]}$

where t² − x² − y² − z² is the minkowski metric^{[note 18]} and Ω is the four-wave-number. If it were possible to design a spectrum analyzer in four dimensions, then one could generalize the idea of switching back and forth between the time domain and the frequency domain. Instead, one would switch between the spacetime domain and the energy-momentum domain. This carries over to general relativity as well. The most user-friendly version of this theory is called Schwarzschild spacetime.^{[note 19]} In that case, the Fourier transform is defined also, as long as one stays outside of the photon sphere. The frequency decreases as one climbs up out of the potential well,^{[note 20]} and therefore one may define a Schwarzschild four-wave-number S. Therefore the transformer becomes

$\,e^{iS[\sqrt{\left(1 - \frac{r_s}{r} \right) c^2 dt^2 - \left(1-\frac{r_s}{r}\right)^{-1} dr^2 - r^2 \left(d\theta^2 + \sin^2\theta \, d\varphi^2\right)}]}$

This generalizes to the next most user-friendly version, which is the Schwarzschild spacetime with a spinning mass and also possibly charged. This is more realistic, because it would seem extremely unlikely that a star would be completely static. But this is beyond the scope of this article.

There are many communications studies which employ the time domain on one axis, and the frequency domain on the other axis. This is two dimensional. Generalizing to spacetime on one axis and energy-momentum on the other is eight dimensional. If one is willing to abandon ordinary geometry and go to this symplectic geometry, then one still has a metric space.^{[note 21]} So one may also define

$\,e^{i[t\cdot E - x\cdot p]/one}$

where t is one dimensional time, E is one dimensional energy, x is three dimensional space, p is three dimensional momentum, and one is 1 Joule second, in order to make the units come out right.

Duality and lattice theory

The lattice of divisors of the number 60.

In the previous section, one switches back and forth between a basis and its mirror image. Duality theorists take this concept further. They work at rephrasing the totality of science in terms of mirror images. The main idea is expressed in lattice theory. If there exists a set of nested structures, then there exists an algebra as well, with union and intersection playing the role of algebraic operations. Now if one reverses the role of the operations, and also reverses the nesting structure, then one has a dual structure. To reverse the nesting structure means that less-than becomes greater-than, and vice-versa; or whatever it was that caused the nesting sequence is reversed; it could be some abstract idea. The entire structure becomes the opposite of what it was.

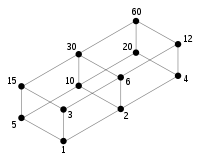
For example, in the image at the right, one has the lattice of integers that divide the number 60. Now if one considers the lattice of fractions that divide the number 1/60th, then this would be the dual lattice. Even though 1/3rd is more than 1/60th, it still divides it. The next section considers the concept of generalizing this dual idea.

Fractional transformations

A fractional transform is one that rotates around a circle. For instance, the ordinary Fourier transform can be applied at most four times before it starts repeating. In some cases, it will start repeating after only two times. But the fractional transform repeats after a thousand times; it goes around in a circle. Unfortunately it is poorly named, and will be called a rotational transform for the remainder of this article.

These rotational transforms are connected to the theory of Riemann surfaces. For instance, e^ix is a circle, but the inverse function ln(z) is not one-to-one. This can be solved by allowing ln(z) to operate on a helical surface instead.^{[note 22]} Similarly, the rotational transforms are parameterized by a circle, but the inverse rotational transform is not one-to-one. This can be solved by interpreting the input as a helix as well.

There has been some consideration of applying the helix idea to dual lattices. The prototypical example of a lattice is a Hasse diagram. The leave-it-the-same or reverse-it operations can be though of as the numbers +1 and -1 on the unit circle. This dual structure is now replaced with the circle, which is in turn replaced with a helix. There are various way to approach this problem.

One way is to think of the signal strength on a cell phone, or on the list of wireless connections on a computer. There will four or five bars. They don't appear like this:

signal strength	1	2	3	4	5
number of bars	-....	.-...	..-..	...-.	....-

but rather like this

signal strength	1	2	3	4	5
number of bars	-....	--...	---..	----.	-----

This means that they are nested, in some sense. If one is getting 4 bars, then they are still getting 3 bars as well. Therefore, because of the nesting structure, the intersection and union of them forms an algebra. For example

[--...] union [---..] = [---..]

and

[--...] intersect [----..] = [--...]

The reverse of this would be the dual lattice.

Another example is provided by the prime numbers: every fraction can be uniquely expressed as a ratio of products of primes. But every fraction can also be expressed uniquely as a ratio of products of these numbers:

$\,\{2, 2*3, 2*3*5, 2*3*5*7 \cdots \}$

For instance

$\,25 = \frac{[2*3*5]^2}{[2*3]^2}$

and

$\,14 = \frac{[2]*[2*3*5*7]}{[2*3*5]}$

A similar idea applies to polynomials. The usual basis for the set of all polynomials is

$\{1, x, x^2, x^3, x^4 \cdots \}$

However if one constructs the following basis instead

$\{1, 1 + x, 1 + x + x^2, 1 + x + x^2 + x^3 \cdots \}$

then it has a lattice structure, because each subspace is inside the next one.

One notices that the Fourier transform is not immediately apparent in the previous examples. It can be brought in by thinking in the very same way of a set of frequencies. The usual basis for the frequency domain is

$\{e^{inx} \quad| \quad n \in \mathbb{R}\}$

If one constructs this basis instead

$\Big\{\int_{0}^{n=\theta} e^{i n x} dn \quad | \quad \theta \in \mathbb{R}\Big\}$

then it is nested, and it can be turned into a lattice. The Fourier transform exchanges frequency/time, convolution/multiplication, gcd/lcm, [p mod q]/[q mod p], and so forth. This is the same as turning the lattice upside down, or turning subset into superset. Making this into a rotational helix is analogous to making the circle into a helix for the inverse rotational transforms.

Dual categories

One possible way of unifying these ideas is to employ the fluffy and abstract notions of category theory. There are the ideas of opposite category and dual category. This means the structures are reversed, as well as the operations. One finds that many dual structures become the same in this case. Often there is only one statement, but many different versions of it. This in turn allows one to prove many different theorems at once.

For instance, one might consider the following table:

proposition	dual
$\mathfrak{F}\{f*g\} = \mathfrak{F}\{f\} \cdot \mathfrak{F}\{g\}$	$\mathfrak{F}\{f \cdot g\}= \mathfrak{F}\{f\}*\mathfrak{F}\{g\}$
$\,\text{ not} (a \text{ and } b) = \text{ not } a \text{ or}\text{ not } b$	$\,\text{ not} (a \text{ or }b) = \text{ not } a \text{ and}\text{ not } b$
$\,\overline{(a \cap b)} = \overline{a} \cup \overline{b}$	$\,\overline{(a \cup b)} = \overline{a} \cap \overline{b}$
$\,\gcd(a,b)^{-1} = \operatorname{lcm}(a^{-1},b^{-1})$	$\,\operatorname{lcm}(a,b)^{-1} = \gcd(a^{-1},b^{-1})$

where the overbar stands for the complement of a set, the dot is pointwise multiplication, and the star is convolution. (GCD and LCM are still defined on the set of fractions, although one may have to work out a few examples to convince oneself that this is true). But as one studies the table, one can see that there is essentially only one statement here, and that the mirror images on the right are the dual statements.

As another example, one might consider the complex fractions.^{[note 23]} One finds that GCD and LCM are defined for them as well. So one may form the infinite lattice of divisors, just as one would for the real fractions. The added benefit here is that these can be mapped to the Riemann sphere, so that the dual map just reflects about the equator. As one adds more and more irrational roots of unity to the complex fractions, they converge to a finer topology, and one arrives at interesting symmetries in number theory. In this way, the function 1/z plays the role of an abstract Fourier transform, and everything else is the same. In technical jargon, one would say that 1/z is a decategorified Fourier transform.

Thus, many results from ordinary mathematics can be proved in more interesting categories. It might be hoped that the electric and magnetic fields would fit neatly into this particular framework as well, but unfortunately this is not the case. It is now felt by many that "nature does not seem to display exact electromagnetic duality".^[1]

The modern world

Phased antenna arrays

Antenna theory has improved over the years. Instead of just throwing a wire out the window, people are now using antenna arrays. Interference is sometimes thought of as a nuisance, but it can also be a good thing. For instance, if one transmits with a hypothetical omnidirectional antenna, the signal will be transmitted in all directions equally. This might be considered wasteful or non-optimal. If instead, one transmits the very same message with two different antennas, there will be a clearly defined interference pattern, with a stronger signal in some directions, and a weaker signal in others. By using more and more antennas, the radiation pattern can be made very precise. And because the transmit pattern is the same as the reception pattern, it allows them to receive in precise directions as well. In addition, the arrays are able to adjust themselves for better reception. This is where the term adaptive antenna array comes from. It is accomplished with various optimization techniques.

Digital radio

Some of the articles on Wikipedia say that certain things are a little easier with digital radio. This is not correct. The truth is that one achieves spectacularly superior results will digital radio, than one could ever achieve with pure analog circuits alone. This is because the filtering techniques, radiation patterns, gain, impedance matching, and almost everything else can be revised by a programmer quite easily. In many cases, it can be revised by the program itself quite easily. The code may be written in C, or in some low level assembly language. An as example, one may imagine trying to log on to Wikipedia with just analog circuits.

However, it is important to realize that even the best programmer should have some knowledge of analog design, because the two concepts work together. Often there is a group of people who are trained in analog, and a separate group who are trained in programming. The best possible scenario would be if each employee had a working knowledge of both, with a few who were expert in one or the other.

System-on-a-chip

A field-programmable gate array.

Things have come a long way from the days of spark-gap transmitters. The system on a chip is a set-up for integrating all the components of an electronics system into a single integrated circuit.^[8] Researchers have also considered systems that employ multiple processor cores.^[9] These provide the ability to easily change the functioning of a powerful system in many useful ways. Also there are many suppliers online. Other related technologies are field-programmable gate arrays that offer "partial reconfigurability",^[10] and the network-on-chip technology.^[11][12]

Neural networks and AI

Neural networks are the wave of the future. They start with no knowledge, and learn from experience. Often there is no reason for them to stop learning, which means they can accumulate a vast amount of experience. Radar and antenna systems are much more capable and powerful in this way, and sometimes better at making decisions than a human. There is a large amount of research on neural networks in communications theory today.^[13] It is only one type of artificial intelligence. Other techniques have been applied to large arrays of MIMO systems. These include estimation theory and Markov chains.^[14] Quantum particle swarm optimization is another approach.^[15] Another is the stochastic pooling network. It is said to be "applicable to examples in biological neural coding, nano-electronics, distributed sensor networks, digital beamforming arrays, image processing, [and] multiaccess communication".^[16]

See also

• Flag - example of a nested structure
• Nest algebra - example of a noncommutative nested structure
• Chirplet transform - a more recently introduced transform
• FIR filter - a popular filter
• IIR filter - almost the same, except it incorporates feedback
• Pontryagin duality - a more comprehensive Fourier theory
• T-duality - a duality for vibrating strings

Notes

1. ^ This is usually called the amplitude. It is the counterpart of volume in sound waves.
2. ^ It might also change how much "gravity" each one has. This is covered more clearly in footnote number 8.
3. ^ Sometimes the voltage and current are written as vectors, but there is no problem in writing them as matrices as well.
4. ^ The star does not appear in those formulas, because that fine article only covers the case with real coefficients.
5. ^ A proof that this mapping is equivalent to a rotation can be found in the article on quaternions and spatial rotations. The proof for the Lorentz boosts is almost identical. Then the transformed version of $q\overline{q}$ is itself. The proof is easy, but it isn't necessary to bother the reader with it here.
6. ^ Some of the + and - signs are different in this article.
7. ^ This is an unusual kind of interference, as talked about later.
8. ^ This includes functions of the form $\lim_{n\to\infty} z^{\pm n}$. In addition, there are linear terms that help to determine them as well. These can be thought of as gravitational attraction (and repulsion if it exists), but they are really part and parcel of the poles and zeros. For example one might have (x-3)/(x-4). Now one could change it to (x-3)/(5x-4). This means that the pole has a stronger "gravity" so to speak. But one could also change it to (x-3)/(0x-4), and that would erase the pole entirely.
9. ^ It's better to make them clear for this article, therefore some of the technical details are incorrect here. For the interested reader, the exact statements are found in the articles.
10. ^ This applies to each point in a domain, so the function would be holomorphic on that domain.
11. ^ Compact here means that every convergent sequence has a limit point in the space, so that every sequence converges, and one can always do calculus.
12. ^ or increases its "gravity" or "anti-gravity"; as before, see footnote number 8.
13. ^ A topologist is a person who cannot tell a coffee cup from a donut.
14. ^ A group has to follow some other rules also, but invertible matrices is the important idea.
15. ^ If the matrix is more than one dimensional, then the variable has to be replaced by a vector space.
16. ^ They are really linear operators, which are essentially the same thing as matrices, where the dimension is allowed to be either infinite or continuously infinite. In this case, the theory has some different fine print involved.
17. ^ This is really a direct integral, which is the differentiable counterpart of a direct sum.
18. ^ The square root will never introduce complex numbers, because the minkowski metric is always positive. This is true as long as one remains in the positive light cone, which one always will in classical studies.
19. ^ as long as one considers the orbiting masses to have zero mass in comparison to the star, which they often do.
20. ^ This particular reason for the frequency warping has been challenged; however the decrease in frequency is well-known and fully verified, so it is solid for this article.
21. ^ This just means that it is still possible to define the notion of distance.
22. ^ There are many ways of saying this. In the article on complex logarithm, a new surface is constructed which serves as the input to ln(z), and is called the Riemann surface of ln(z).
23. ^ It's best to start with the complex integers, and then form the field of fractions. Almost every aspect of the ordinary integers is represented here.

References

1. ^ ^{a b} David Olive, Exact Electromagnetic Duality, www.arxiv.org/abs/9508089
2. ^ Y. Friedman and S. Gwertzman, The scalar complex potential of the electromagnetic field (2009), www.arxiv.org/abs/0906.0930 Section III
3. ^ M. Greiter, D. Schuricht, Imaginary in all directions: an elegant formulation of special relativity and classical electrodynamics, www.arxiv.org/abs/0309061
4. ^ Zihua Weng, Compounding Fields and Their Quantum Equations in the Trigintaduonion Space, www.arxiv.org/abs/0704.0136
5. ^ P. S. Bisht, O. P. S. Negi, Spontaneous Symmetry Breaking in Presence of Electric and Magnetic Charges, www.arxiv.org/abs/1011.3921
6. ^ K. Lechner and P.A. Marchetti, Spin-statistics transmutation in relativistic quantum field theories of dyons (2000), arxiv.org/abs/hep-th/0010291, see page 2
7. ^ ^{a b} H. Dehnen, O. P. S. Negi, Electromagnetic Duality, Quaternion and Supersymmetric Gauge Theories of Dyons, www.arxiv.org/abs/0608164
8. ^ Mohd Abubakr, Frequency Analysis of Decoupling Capacitors for Three Voltage Supplies in SoC (2007), www.arxiv.org/abs/0710.3789
9. ^ H. Siebert, Debug Support, Calibration and Emulation for Multiple Processor and Powertrain Control SoCs (2007), www.arxiv.org/abs/0710.4827
10. ^ Ji Ding, and Juergen Teich and Sandor P. Fekete and Jan van der Veen, A Practical Approach for Circuit Routing on Dynamic Reconfigurable Devices (2005), www.arxiv.org/abs/cs/0503066
11. ^ Philippe Martin, Design of a Virtual Component Neutral Network-on-Chip Transaction Layer (2007), www.arxiv.org/abs/0710.4754
12. ^ Leandro Moller, Ney Calazans et al., A Multiprocessing System Enabled by a Network on Chip (2007), www.arxiv.org/abs/0710.4843
13. ^ T. Kosel and I. Grabec, Intelligent location of simultaneously active acoustic emission sources: Part I (2007), www.arxiv.org/abs/0704.0047
14. ^ Saif K. Mohammed, Ahmed Zaki, et al., High-Rate Space-Time Coded Large MIMO Systems: Low-Complexity Detection and Channel Estimation (2008), www.arxiv.org/abs/0809.2446
15. ^ Said Mikki and Ahmed A. Kishk, Quantum Particle Swarm Optimization for Electromagnetics (2007), www.arxiv.org/abs/physics/0702214
16. ^ M. McDonnell, P. Amblard and N. Stocks, Stochastic Pooling Networks (2009), www.arxiv.org/abs/0901.3644