Pole (complex analysis)

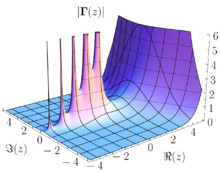The absolute value of the Gamma function. This shows that a function becomes infinite at the poles (left). On the right, the Gamma function does not have poles, it just increases quickly.

In the mathematical field of complex analysis, a pole of a meromorphic function is a certain type of singularity that behaves like the singularity of $\scriptstyle \frac{1}{z^n}$ at z = 0. This means that, in particular, a pole of the function f(z) is a point a such that f(z) approaches infinity as z approaches a.

Definition

Formally, suppose U is an open subset of the complex plane C, a is an element of U and f : U \ {a} → C is a function which is holomorphic over its domain. If there exists a holomorphic function g : U → C and a positive integer n, such that for all z in U \ {a}

$f(z) = \frac{g(z)}{(z-a)^n}$

holds, then a is called a pole of f. The smallest such n is called the order of the pole. A pole of order 1 is called a simple pole.

A few authors allow the order of a pole to be zero, in which case a pole of order zero is either a regular point or a removable singularity. However, it is more usual to require the order of a pole to be positive.

From above several equivalent characterizations can be deduced:

If n is the order of pole a, then necessarily g(a) ≠ 0 for the function g in the above expression. So we can put

$f(z) = \frac{1}{h(z)}$

for some h that is holomorphic in an open neighborhood of a and has a zero of order n at a. So informally one might say that poles occur as reciprocals of zeros of holomorphic functions.

Also, by the holomorphy of g, f can be expressed as:

$f(z) = \frac{a_{-n}}{ (z - a)^n } + \cdots + \frac{a_{-1}}{ (z - a) } + \sum_{k\, \geq \,0} a_k (z - a)^k.$

This is a Laurent series with finite principal part. The holomorphic function $\scriptstyle \sum_{k\,\ge\,0} a_k(z\, - \,a)^k$ (on U) is called the regular part of f. So the point a is a pole of order n of f if and only if all the terms in the Laurent series expansion of f around a below degree −n vanish and the term in degree −n is not zero.

Pole at infinity

It can be defined for a complex function the notion of having a pole at the point at infinity. In this case U has to be a neighborhood of infinity. For example, the exterior of any closed ball. Now, for using the previous definition a meaning for g being holomorphic at ∞ should be given and also for the notion of "having" a zero at infinity as $\scriptstyle z\, - \,a$ does at the finite point a. Instead a definition can be given starting from the definition at a finite point by "bringing" the point at infinity to a finite point. The map $\scriptstyle z\, \mapsto \,\frac{1}{z}$ does that. Then, by definition, a function, f, holomorphic in a neighborhood of infinity has a pole at infinity if the function $\scriptstyle f(\frac{1}{z})$ (which will be holomorphic in a neighborhood of $\scriptstyle z\,=\,0$), has a pole at $\scriptstyle z\,=\,0$, the order of which will be taken as the order of the pole at infinity.

Pole of a function on a complex manifold

In general, having a function $\scriptstyle f:\; M\, \rightarrow \,\mathbb{C}$ that is holomorphic in a neighborhood, $\scriptstyle U$, of the point $\scriptstyle a$, in the complex manifold M, it is said that f has a pole at a of order n if, having a chart $\scriptstyle \phi:\; U\, \rightarrow \,\mathbb{C}$, the function $\scriptstyle f\, \circ \,\phi^{-1}:\; \mathbb{C}\, \rightarrow \,\mathbb{C}$ has a pole of order n at $\scriptstyle \phi(a)$ (which can be taken as being zero if a convenient choice of the chart is made). ] The pole at infinity is the simplest nontrivial example of this definition in which M is taken to be the Riemann sphere and the chart is taken to be $\scriptstyle \phi(z)\, = \,\frac{1}{z}$.

Examples

• The function

$f(z) = \frac{3}{z}$

has a pole of order 1 or simple pole at $\scriptstyle z\, = \,0$.

• The function

$f(z) = \frac{z+2}{(z-5)^2(z+7)^3}$

has a pole of order 2 at $\scriptstyle z\, = \,5$ and a pole of order 3 at $\scriptstyle z\, = \,-7$.

• The function

$f(z) = \frac{z-4}{e^z-1}$

has poles of order 1 at $\scriptstyle z\, = \,2\pi ni\text{ for } n\, = \,\dots,\, -1,\, 0,\, 1,\, \dots.$ To see that, write $\scriptstyle e^z$ in Taylor series around the origin.

• The function

f(z) = z

has a single pole at infinity of order 1.

Terminology and generalisations

If the first derivative of a function f has a simple pole at a, then a is a branch point of f. (The converse need not be true).

A non-removable singularity that is not a pole or a branch point is called an essential singularity.

A complex function which is holomorphic except for some isolated singularities and whose only singularities are poles is called meromorphic.

See also

• Control theory#Stability
• Filter design
• Filter (signal processing)
• Nyquist stability criterion
• Pole–zero plot
• Residue (complex analysis)
• Zero (complex analysis)

External links

• Weisstein, Eric W., "Pole" from MathWorld.
• Module for Zeros and Poles by John H. Mathews