- Lorentz transformation
-
 A visualisation of the Lorentz transformation (full animation). Only one space coordinate is considered. The thin solid lines crossing at right angles depict the time and distance coordinates of an observer at rest with respect to that frame; the skewed solid straight lines depict the coordinate grid of an observer moving with respect to that same frame.
A visualisation of the Lorentz transformation (full animation). Only one space coordinate is considered. The thin solid lines crossing at right angles depict the time and distance coordinates of an observer at rest with respect to that frame; the skewed solid straight lines depict the coordinate grid of an observer moving with respect to that same frame.In physics, the Lorentz transformation or Lorentz-Fitzgerald transformation describes how, according to the theory of special relativity, two observers' varying measurements of space and time can be converted into each other's frames of reference. It is named after the Dutch physicist Hendrik Lorentz. It reflects the surprising fact that observers moving at different velocities may measure different distances, elapsed times, and even different orderings of events.
The Lorentz transformation was originally the result of attempts by Lorentz and others to explain how the speed of light was observed to be independent of the reference frame, and to understand the symmetries of the laws of electromagnetism. Albert Einstein later re-derived the transformation from his postulates of special relativity. The Lorentz transformation supersedes the Galilean transformation of Newtonian physics, which assumes an absolute space and time (see Galilean relativity). According to special relativity, this is a good approximation only at relative speeds much smaller than the speed of light.
If space is homogeneous, then the Lorentz transformation must be a linear transformation. Also, since relativity postulates that the speed of light is the same for all observers, it must preserve the spacetime interval between any two events in Minkowski space. The Lorentz transformation describes only the transformations in which the spacetime event at the origin is left fixed, so they can be considered as a hyperbolic rotation of Minkowski space. The more general set of transformations that also includes translations is known as the Poincaré group.
History
- See also History of Lorentz transformations.
Many physicists, including George FitzGerald, Joseph Larmor, Hendrik Lorentz and Woldemar Voigt, had been discussing the physics behind these equations since 1887.[1][2] Larmor and Lorentz, who believed the luminiferous ether hypothesis, were seeking the transformation under which Maxwell's equations were invariant when transformed from the ether to a moving frame. Early in 1889, Oliver Heaviside had shown from Maxwell's equations that the electric field surrounding a spherical distribution of charge should cease to have spherical symmetry once the charge is in motion relative to the ether. FitzGerald then conjectured that Heaviside’s distortion result might be applied to a theory of intermolecular forces. Some months later, FitzGerald published his conjecture in Science to explain the baffling outcome of the 1887 ether-wind experiment of Michelson and Morley. This idea was extended by Lorentz[3] and Larmor[4] over several years, and became known as the FitzGerald-Lorentz explanation of the Michelson-Morley null result, known early on through the writings of Lodge, Lorentz, Larmor, and FitzGerald.[5] Their explanation was widely known before 1905.[6] Larmor is also credited to have been the first to understand the crucial time dilation property inherent in his equations.[7]
In 1905, Henri Poincaré was the first to recognize that the transformation has the properties of a mathematical group, and named it after Lorentz.[8] Later in the same year Einstein derived the Lorentz transformation under the assumptions of the principle of relativity and the constancy of the speed of light in any inertial reference frame,[9] obtaining results that were algebraically equivalent to Larmor's (1897) and Lorentz's (1899, 1904), but with a different interpretation.
Paul Langevin (1911) said of the transformation:[10]
- "It is the great merit of H. A. Lorentz to have seen that the fundamental equations of electromagnetism admit a group of transformations which enables them to have the same form when one passes from one frame of reference to another; this new transformation has the most profound implications for the transformations of space and time".
Lorentz transformation for frames in standard configuration
Consider two observers O and O' , each using their own Cartesian coordinate system to measure space and time intervals. O uses (t, x, y, z) and O ' uses (t' , x' , y' , z' ). Assume further that the coordinate systems are oriented so that the x-axis and the x' -axis are collinear, the y-axis is parallel to the y' -axis, as are the z-axis and the z' -axis. The relative velocity between the two observers is v along the common x-axis. Also assume that the origins of both coordinate systems are the same. If all these hold, then the coordinate systems are said to be in standard configuration. A symmetric presentation between the forward Lorentz Transformation and the inverse Lorentz Transformation can be achieved if coordinate systems are in symmetric configuration. The symmetric form highlights that all physical laws should be of such a kind that they remain unchanged under a Lorentz transformation.
The Lorentz transformation for frames in standard configuration can be shown to be:
where

is called the Lorentz factor.
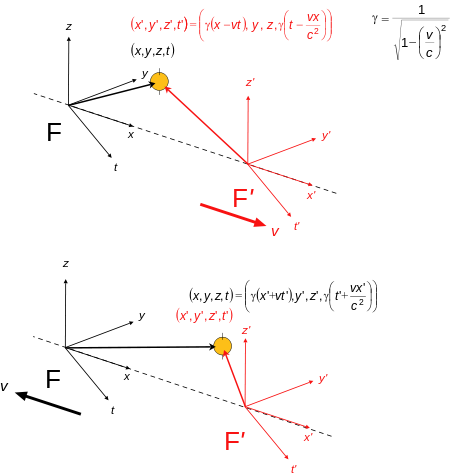 The space-time coordinates of a particle (also in standard configuration); as measured by each observer in their inertial reference frame. Top: the red frame F' moves at velocity v in the +x direction relative to the black frame F, the observer in F measures the position of the particle (or any event at that space-time coordinate) using the F coordinate system. Bottom: the black frame F moves at velocity v in the -x direction relative to the red frame F', the observer in F measures the position of the particle (or event) using the F coordinate system. Notice the symmetry between the apparently different situations from the view of the diagram.
The space-time coordinates of a particle (also in standard configuration); as measured by each observer in their inertial reference frame. Top: the red frame F' moves at velocity v in the +x direction relative to the black frame F, the observer in F measures the position of the particle (or any event at that space-time coordinate) using the F coordinate system. Bottom: the black frame F moves at velocity v in the -x direction relative to the red frame F', the observer in F measures the position of the particle (or event) using the F coordinate system. Notice the symmetry between the apparently different situations from the view of the diagram.
Matrix form
Boost in x, y or z directions
These Lorentz transformations are called "boosts" in the given direction.
For a boost in the x-direction, we have:
which is equivalent to the set of equations in the previous section, with

Similarly for a boost in the y-direction:
and the z-direction:
Sometimes capital lambda Λ is used for one of the above matrices corresponding to the required direction, often R is used for the four-position,

The Lorentz transform for a boost in one of the above directions can be compactly written as a single matrix equation:
Here the transformation has been applied to the four-position, though this transformation matrix is universal for all four-vectors. That is, if A is any four-vector, then:
Boost in any direction
More generally for a boost in any arbitrary direction at velocity v = (vx, vy, vz), or equivalently β = (βx, βy, βz) ,
where


 , and
, and 
Although the matrix is symmetric, it appears daunting and unwieldy. To make it easier to remember and use, we could introduce another factor capital beta Β:

(in which i and j can each be set to x, y or z, or using index notation, 1 replaces subscript x, similarly 2 replaces subscript y and 3 replaces subscript z), so:

Note that this transformation is only the "boost," i.e., a transformation between two frames whose x, y, and z axis are parallel and whose spacetime origins coincide (see The "Standard configuration" Figure). The most general proper Lorentz transformation also contains a rotation of the three axes, because the composition of two boosts is not a pure boost but is a boost followed by a rotation. The rotation gives rise to Thomas precession. The boost is given by a symmetric matrix, but the general Lorentz transformation matrix need not be symmetric.
Composition of two boosts
The composition of two Lorentz boosts B(u) and B(v) of velocities u and v is given by:[11][12]
![B(\mathbf{u})B(\mathbf{v})=B\left ( \mathbf{u}\oplus\mathbf{v} \right )\mathrm{Gyr}\left [ \mathbf{u},\mathbf{v}\right ]=\mathrm{Gyr}\left [\mathbf{u},\mathbf{v} \right ]B \left ( \mathbf{v}\oplus\mathbf{u} \right )](f/43f8fda5a85940fee8a6b5050569489b.png) ,
,
where
 is the velocity-addition, and Gyr[u,v] (capital G) is the rotation arising from the composition, gyr (lower case g) being the gyrovector space abstraction of the gyroscopic Thomas precession, and B(v) is the 4x4 matrix that uses the components of v, i.e. v1, v2, v3 in the entries of the matrix, or rather the components of v/c in the representation that is used above.
is the velocity-addition, and Gyr[u,v] (capital G) is the rotation arising from the composition, gyr (lower case g) being the gyrovector space abstraction of the gyroscopic Thomas precession, and B(v) is the 4x4 matrix that uses the components of v, i.e. v1, v2, v3 in the entries of the matrix, or rather the components of v/c in the representation that is used above.The composition of two Lorentz transformations L(u,U) and L(v,V) which include rotations U and V is given by:[13]
If the 3x3 matrix form of the rotation applied to spatial coordinates is given by gyr[u,v], then the 4x4 matrix rotation applied to 4-coordinates is given by:
![\mathrm{Gyr}[\mathbf{u},\mathbf{v}]=
\begin{pmatrix}
1 & 0 \\
0 & \mathrm{gyr}[\mathbf{u},\mathbf{v}]
\end{pmatrix}](f/4af13753bd55f7284f62e0d44f6e39f3.png) .[11]
.[11]
 Views of spacetime along the world line of a rapidly accelerating observer (center) moving in a 1-dimensional (straight line) "universe". The vertical direction indicates time, while the horizontal indicates distance, the dashed line is the spacetime trajectory ("world line") of the observer. The small dots are specific events in spacetime. If one imagines these events to be the flashing of a light, then the events that pass the two diagonal lines in the bottom half of the image (the past light cone of the observer in the origin) are the events visible to the observer. The slope of the world line (deviation from being vertical) gives the relative velocity to the observer. Note how the view of spacetime changes when the observer accelerates.
Views of spacetime along the world line of a rapidly accelerating observer (center) moving in a 1-dimensional (straight line) "universe". The vertical direction indicates time, while the horizontal indicates distance, the dashed line is the spacetime trajectory ("world line") of the observer. The small dots are specific events in spacetime. If one imagines these events to be the flashing of a light, then the events that pass the two diagonal lines in the bottom half of the image (the past light cone of the observer in the origin) are the events visible to the observer. The slope of the world line (deviation from being vertical) gives the relative velocity to the observer. Note how the view of spacetime changes when the observer accelerates.For a boost in an arbitrary direction with velocity
 , it is convenient to decompose the spatial vector
, it is convenient to decompose the spatial vector  into components perpendicular and parallel to the velocity
into components perpendicular and parallel to the velocity  :
:  . Then only the component
. Then only the component  in the direction of
in the direction of  is 'warped' by the gamma factor:
is 'warped' by the gamma factor:where now
 . The second of these can be written as:
. The second of these can be written as:These equations can be expressed in matrix form as
where I is the identity matrix, v is velocity written as a column vector, vT is its transpose (a row vector) and
 is its versor.
is its versor.Rapidity
The Lorentz transformation can be cast into another useful form by defining a parameter
 called the rapidity (an instance of hyperbolic angle) such that
called the rapidity (an instance of hyperbolic angle) such thatso that
Equivalently:
Then the Lorentz transformation in standard configuration is:
Hyperbolic trigonometric expressions
From the above expressions for eφ and e−φ
and therefore,
Hyperbolic rotation of coordinates
Substituting these expressions into the matrix form of the transformation, we have:
Thus, the Lorentz transformation can be seen as a hyperbolic rotation of coordinates in Minkowski space, where the parameter ϕ represents the hyperbolic angle of rotation, often referred to as rapidity. This transformation is sometimes illustrated with a Minkowski diagram.
Lorentz transformation of the electromagnetic field
The fact that the electromagnetic field shows relativistic effects becomes clear by carrying out a simple thought experiment:
- Consider an observer measuring a charge at rest in a reference frame F. The observer will detect a static electric field. As the charge is stationary in this frame, there is no electric current, so the observer will not observe any magnetic field.
- If another observer in frame F' moving at relative velocity v (to F and the charge), this observer will notice the electric field changing as a result of relative motion, in addition interpret the charge in motion travelling at relative velocity −v (to F') as an electric current having a magnetic field around it.
This shows that the Lorentz transformation also applies to electromagnetic field quantities when changing the frame of reference.
For the electric and magnetic field quantities, the following transformations apply:[14]
These formulae can be summarized in the matrix:
In non-relativistic approximation, i. e. for speeds
 , the relativistic factor
, the relativistic factor  , so that there is no need to distinguish between the spatial and temporal coordinates in Maxwell's equations. This yields the following transformations:
, so that there is no need to distinguish between the spatial and temporal coordinates in Maxwell's equations. This yields the following transformations:Spacetime interval
In a given coordinate system (xμ), if two events A and B are separated by
the spacetime interval between them is given by
This can be written in another form using the Minkowski metric. In this coordinate system,
Then, we can write
or, using the Einstein summation convention,
Now suppose that we make a coordinate transformation
 . Then, the interval in this coordinate system is given by
. Then, the interval in this coordinate system is given byor
It is a result of special relativity that the interval is an invariant. That is,
 . It can be shown[15] that this requires the coordinate transformation to be of the form
. It can be shown[15] that this requires the coordinate transformation to be of the formHere,
 is a constant vector and
is a constant vector and  a constant matrix, where we require that
a constant matrix, where we require thatSuch a transformation is called a Poincaré transformation or an inhomogeneous Lorentz transformation.[16] The Ca represents a spacetime translation. When
 , the transformation is called an homogeneous Lorentz transformation, or simply a Lorentz transformation.
, the transformation is called an homogeneous Lorentz transformation, or simply a Lorentz transformation.Taking the determinant of
 gives us
gives usLorentz transformations with
 form a subgroup called proper Lorentz transformations which is the special orthogonal group SO(1,3). Those with
form a subgroup called proper Lorentz transformations which is the special orthogonal group SO(1,3). Those with  are called improper Lorentz transformations which is not a subgroup, as the product of any two improper Lorentz transformations will be a proper Lorentz transformation. From the above definition of Λ it can be shown that
are called improper Lorentz transformations which is not a subgroup, as the product of any two improper Lorentz transformations will be a proper Lorentz transformation. From the above definition of Λ it can be shown that  , so either
, so either  or
or  , called orthochronous and non-orthochronous respectively. An important subgroup of the proper Lorentz transformations are the proper orthochronous Lorentz transformations which consist purely of boosts and rotations. Any Lorentz transform can be written as a proper orthochronous, together with one or both of the two discrete transformations; space inversion (P) and time reversal (T), whose non-zero elements are:
, called orthochronous and non-orthochronous respectively. An important subgroup of the proper Lorentz transformations are the proper orthochronous Lorentz transformations which consist purely of boosts and rotations. Any Lorentz transform can be written as a proper orthochronous, together with one or both of the two discrete transformations; space inversion (P) and time reversal (T), whose non-zero elements are:The set of Poincaré transformations satisfies the properties of a group and is called the Poincaré group. Under the Erlangen program, Minkowski space can be viewed as the geometry defined by the Poincaré group, which combines Lorentz transformations with translations. In a similar way, the set of all Lorentz transformations forms a group, called the Lorentz group.
A quantity invariant under Lorentz transformations is known as a Lorentz scalar.
Special relativity
One of the most astounding consequences of Einstein's clock-setting method is the idea that time is relative. In essence, each observer's frame of reference is associated with a unique set of clocks, the result being that time passes at different rates for different observers. This was a direct result of the Lorentz transformations and is called time dilation. We can also clearly see from the Lorentz "local time" transformation that the concept of the relativity of simultaneity and of the relativity of length contraction are also consequences of that clock-setting hypothesis.
Lorentz transformations can also be used to prove that magnetic and electric fields are simply different aspects of the same force — the electromagnetic force. If we have one charge or a collection of charges which are all stationary with respect to each other, we can observe the system in a frame in which there is no motion of the charges. In this frame, there is only an "electric field". If we switch to a moving frame, the Lorentz transformation will predict that a "magnetic field" is present. This field was initially unified in Maxwell's concept of the "electromagnetic field".
The correspondence principle
For relative speeds much less than the speed of light, the Lorentz transformations reduce to the Galilean transformation in accordance with the correspondence principle.
The correspondence limit is usually stated mathematically as: as
 ,
,  . In words: as velocity approaches 0, the speed of light (seems to) approach infinity. Hence, it is sometimes said that nonrelativistic physics is a physics of "instant action at a distance".
. In words: as velocity approaches 0, the speed of light (seems to) approach infinity. Hence, it is sometimes said that nonrelativistic physics is a physics of "instant action at a distance".Derivation
The usual treatment (e.g., Einstein's original work) is based on the invariance of the speed of light. However, this is not necessarily the starting point: indeed (as is exposed, for example, in the second volume of the Course of Theoretical Physics by Landau and Lifshitz), what is really at stake is the locality of interactions: one supposes that the influence that one particle, say, exerts on another can not be transmitted instantaneously. Hence, there exists a theoretical maximal speed of information transmission which must be invariant, and it turns out that this speed coincides with the speed of light in vacuum. The need for locality in physical theories was already noted by Newton (see Koestler's The Sleepwalkers), who considered the notion of an action at a distance "philosophically absurd" and believed that gravity must be transmitted by an agent (such as an interstellar aether) which obeys certain physical laws.
Michelson and Morley in 1887 designed an experiment, employing an interferometer and a half-silvered mirror, that was accurate enough to detect aether flow. The mirror system reflected the light back into the interferometer. If there were an aether drift, it would produce a phase shift and a change in the interference that would be detected. However, no phase shift was ever found. The negative outcome of the Michelson-Morley experiment left the concept of aether (or its drift) undermined. There was consequent perplexity as to why light evidently behaves like a wave, without any detectable medium through which wave activity might propagate.
In a 1964 paper,[17] Erik Christopher Zeeman showed that the causality preserving property, a condition that is weaker in a mathematical sense than the invariance of the speed of light, is enough to assure that the coordinate transformations are the Lorentz transformations.
From group postulates
Following is a classical derivation (see, e.g., [1] and references therein) based on group postulates and isotropy of the space.
Coordinate transformations as a group
The coordinate transformations between inertial frames form a group (called the proper Lorentz group) with the group operation being the composition of transformations (performing one transformation after another). Indeed the four group axioms are satisfied:
- Closure: the composition of two transformations is a transformation: consider a composition of transformations from the inertial frame K to inertial frame K', (denoted as
![[K\to K']](7/1b7556e399257595538f6c8a6d968fe2.png) ), and then from K' to inertial frame K'',
), and then from K' to inertial frame K'', ![[K'\to K'']](1/bb1385dbd227d7fb6a72810f3c7634bd.png) , there exists a transformation,
, there exists a transformation, ![[K\to K'']](1/d616f305cf6d38da653bdce773bdd18d.png) , directly from an inertial frame K to inertial frame K''.
, directly from an inertial frame K to inertial frame K''. - Associativity: the result of
![\big([K\to K'][K'\to K'']\big)[K''\to K''']](8/1989d3a9aa77ebc8e761146fbac0a3fe.png) and
and ![[K\to K']\big([K'\to K''][K''\to K''']\big)](f/dff67f9e28d69032d72bac62984b167e.png) is the same,
is the same,  .
. - Identity element: there is an identity element, a transformation
 .
. - Inverse element: for any transformation
 there exists an inverse transformation
there exists an inverse transformation  .
.
Transformation matrices consistent with group axioms
Let us consider two inertial frames, K and K', the latter moving with velocity
 with respect to the former. By rotations and shifts we can choose the z and z' axes along the relative velocity vector and also that the events (t=0,z=0) and (t'=0,z'=0) coincide. Since the velocity boost is along the z (and z') axes nothing happens to the perpendicular coordinates and we can just omit them for brevity. Now since the transformation we are looking after connects two inertial frames, it has to transform a linear motion in (t,z) into a linear motion in (t',z') coordinates. Therefore it must be a linear transformation. The general form of a linear transformation is
with respect to the former. By rotations and shifts we can choose the z and z' axes along the relative velocity vector and also that the events (t=0,z=0) and (t'=0,z'=0) coincide. Since the velocity boost is along the z (and z') axes nothing happens to the perpendicular coordinates and we can just omit them for brevity. Now since the transformation we are looking after connects two inertial frames, it has to transform a linear motion in (t,z) into a linear motion in (t',z') coordinates. Therefore it must be a linear transformation. The general form of a linear transformation iswhere α,β,γ, and δ are some yet unknown functions of the relative velocity v.
Let us now consider the motion of the origin of the frame K'. In the K' frame it has coordinates (t',z'=0), while in the K frame it has coordinates (t,z=vt). These two points are connected by our transformation
from which we get
 .
.
Analogously, considering the motion of the origin of the frame K, we get
from which we get
 .
.
Combining these two gives α = γ and the transformation matrix has simplified a bit,
Now let us consider the group postulate inverse element. There are two ways we can go from the K' coordinate system to the K coordinate system. The first is to apply the inverse of the transform matrix to the K' coordinates:
The second is, considering that the K' coordinate system is moving at a velocity v relative to the K coordinate system, the K coordinate system must be moving at a velocity − v relative to the K' coordinate system. Replacing v with − v in the transformation matrix gives:
Now the function γ can not depend upon the direction of v because it is apparently the factor which defines the relativistic contraction and time dilation. These two (in an isotropic world of ours) cannot depend upon the direction of v. Thus, γ( − v) = γ(v) and comparing the two matrices, we get
According to the closure group postulate a composition of two coordinate transformations is also a coordinate transformation, thus the product of two of our matrices should also be a matrix of the same form. Transforming K to K' and from K' to K'' gives the following transformation matrix to go from K to K'':
In the original transform matrix, the main diagonal elements are both equal to γ, hence, for the combined transform matrix above to be of the same form as the original transform matrix, the main diagonal elements must also be equal. Equating these elements and rearranging gives:
The denominator will be nonzero for nonzero v as γ(v) is always nonzero, as γ2 + vδγ = 1. If v=0 we have the identity matrix which coincides with putting v=0 in the matrix we get at the end of this derivation for the other values of v, making the final matrix valid for all nonnegative v.
For the nonzero v, this combination of function must be a universal constant, one and the same for all inertial frames. Let's define this constant as
 where
where  has the dimension of 1 / v2. Solving
has the dimension of 1 / v2. Solvingwe finally get
 and thus the transformation matrix, consistent with the group axioms, is given by
and thus the transformation matrix, consistent with the group axioms, is given byIf
 were positive, then there would be transformations (with
were positive, then there would be transformations (with  ) which transform time into a spatial coordinate and vice versa. We exclude this on physical grounds, because time can only run in the positive direction. Thus two types of transformation matrices are consistent with group postulates: i) with the universal constant κ = 0 and ii) with κ < 0.
) which transform time into a spatial coordinate and vice versa. We exclude this on physical grounds, because time can only run in the positive direction. Thus two types of transformation matrices are consistent with group postulates: i) with the universal constant κ = 0 and ii) with κ < 0.Galilean transformations
If
 then we get the Galilean-Newtonian kinematics with the Galilean transformation,
then we get the Galilean-Newtonian kinematics with the Galilean transformation,where time is absolute, t' = t, and the relative velocity v of two inertial frames is not limited.
Lorentz transformations
If
 is negative, then we set
is negative, then we set  which becomes the invariant speed, the speed of light in vacuum. This yields
which becomes the invariant speed, the speed of light in vacuum. This yields  and thus we get special relativity with Lorentz transformation
and thus we get special relativity with Lorentz transformationwhere the speed of light is a finite universal constant determining the highest possible relative velocity between inertial frames.
If
 the Galilean transformation is a good approximation to the Lorentz transformation.
the Galilean transformation is a good approximation to the Lorentz transformation.Only experiment can answer the question which of the two possibilities, κ = 0 or κ < 0, is realised in our world. The experiments measuring the speed of light, first performed by a Danish physicist Ole Rømer, show that it is finite, and the Michelson–Morley experiment showed that it is an absolute speed, and thus that κ < 0.
From physical principles
The problem is usually restricted to two dimensions by using a velocity along the x axis such that the y and z coordinates do not intervene. It is similar to that of Einstein.[18][19] As in the Galilean transformation, the Lorentz transformation is linear since the relative velocity of the reference frames is constant as a vector; otherwise, inertial forces would appear. They are called inertial or Galilean reference frames. According to relativity no Galilean reference frame is privileged. Another condition is that the speed of light must be independent of the reference frame, in practice of the velocity of the light source.
Galilean reference frames
In classical kinematics, the total displacement x in the R frame is the sum of the relative displacement x′ in frame R' and of the distance between the two origins x-x'. If v is the relative velocity of R' relative to R, the transformation is: x = x′ + vt, or x′ = x − vt. This relationship is linear for a constant v, that is when R and R' are Galilean frames of reference.
In Einstein's relativity, the main difference with Galilean relativity is that space is a function of time and vice-versa: t ≠ t′. The most general linear relationship is obtained with four constant coefficients, A, B, γ, and b:
The Lorentz transformation becomes the Galilean transformation when γ = B = 1 , b = -v.
An object at rest in the R frame at position x′=0, will be seen as moving with constant velocity v. Hence the transformation must satisfy x′=0 if x=vt. Therefore, b=-γ v and it may written as:
Principle of relativity
According to the principle of relativity, there is no privileged Galilean frame of reference. Therefore, the inverse transformation for the position from frame R′ to frame R must be
with the same value of γ (which must therefore be an even function of v).
Speed of light independent of the velocity of the source
If the speed of light must be independent of the reference frame, the transformation must ensure that x = ct if x′ = ct′. In other words, the light emitted at t=t′=0 moves at velocity c in both frames. Replacing x and x′ in the preceding equations, one has:
Multiplying these two, one finds
From which
called the "Lorentz factor".
Transformation of time
The factors A and B in the transformation for time can now be obtained. Substituting the derived expression for x′
in the inverse transformation equation
gives
Solving for t′, this results in
and identification with the general transformation
results in
and thus finally in
Extentions
A recent optical experiment reported an interesting result [20]. Three authors performed a modified Fizeau experiment to test the velocity-addition formula of light speed in air flow between still water. The visible shift of interference fringes implies that parameter c in the rule and Lorentz transformation should be replaced by c/n (n=1.33 is refractive index of water in this experiment). It will reduce to that of old Fizeau's experiments and Lorentz transformation in case of n=1(vacuum) or n~1 (air).
See also
- Electromagnetic field
- Galilean transformation
- Hyperbolic rotation
- Invariance mechanics
- Lorentz group
- Principle of relativity
- Velocity-addition formula
- Algebra of physical space
- Relativistic aberration
- Prandtl–Glauert transformation
References
- ^ O'Connor, John J.; Robertson, Edmund F., A History of Special Relativity, http://www-groups.dcs.st-and.ac.uk/~history/HistTopics/Special_relativity.html
- ^ Sinha, Supurna (2000), "Poincaré and the Special Theory of Relativity", Resonance 5 (2): 12–15, doi:10.1007/BF02838818, http://www.ias.ac.in/resonance/Feb2000/pdf/Feb2000p12-15.pdf
- ^ See History of Special Relativity. The work is contained within Lorentz, Hendrik Antoon (1895), Attempt of a Theory of Electrical and Optical Phenomena in Moving Bodies, Leiden, [The Netherlands]: E.J. Brill; Lorentz, Hendrik Antoon (1899), "Simplified Theory of Electrical and Optical Phenomena in Moving Systems", Proc. Acad. Science Amsterdam I: 427–443; and Lorentz, Hendrik Antoon (1904), "Electromagnetic phenomena in a system moving with any velocity smaller than that of light", Proc. Acad. Science Amsterdam IV: 669–678
- ^ Larmor, J. (1897), "On a Dynamical Theory of the Electric and Luminiferous Medium, Part 3, Relations with material media", Philosophical Transactions of the Royal Society 190: 205–300, Bibcode 1897RSPTA.190..205L, doi:10.1098/rsta.1897.0020
- ^ Brown, Harvey R., Michelson, FitzGerald and Lorentz: the Origins of Relativity Revisited, http://philsci-archive.pitt.edu/id/eprint/987
- ^ Rothman, Tony (2006), "Lost in Einstein's Shadow", American Scientist 94 (2): 112f., http://www.americanscientist.org/libraries/documents/200622102452_866.pdf
- ^ Macrossan, Michael N. (1986), "A Note on Relativity Before Einstein", Brit. Journal Philos. Science 37: 232–34, http://espace.library.uq.edu.au/view.php?pid=UQ:9560
- ^ The reference is within the following paper: Poincaré, Henri (1905), "On the Dynamics of the Electron", Comptes rendus hebdomadaires des séances de l'Académie des Sciences 140: 1504–1508
- ^ Einstein, Albert (1905-06-30), "Zur Elektrodynamik bewegter Körper", Annalen der Physik 17 (10): 891–921, Bibcode 1905AnP...322..891E, doi:10.1002/andp.19053221004, http://www.pro-physik.de/Phy/pdfs/ger_890_921.pdf, retrieved 2009-02-02.
- ^ The citation is within the following paper: Langevin, P. (1911), "L'évolution de l'éspace et du temps", Scientia X: 31–54
- ^ a b Ungar, A. A: The relativistic velocity composition paradox and the Thomas rotation. Found. Phys. 19, 1385–1396 (1989)
- ^ The relativistic composite-velocity reciprocity principle, AA Ungar - Foundations of Physics, 2000 - Springer
- ^ eq. (55), Thomas rotation and the parametrization of the Lorentz transformation group, AA Ungar - Foundations of Physics Letters, 1988
- ^ Daniel, Herbert (1997), "4.5.1", Physik: Elektrodynamik, relativistische Physik, Walter de Gruyter, p. 360–361, ISBN 3-110-15777-2, http://books.google.com/books?id=8vAC8YG41goC, Extract of pages 360-361
- ^ Weinberg, Steven (1972), Gravitation and Cosmology, New York, [NY.]: Wiley, ISBN 0-471-92567-5: (Section 2:1)
- ^ Weinberg, Steven (1995), The quantum theory of fields (3 vol.), Cambridge, [England] ; New York, [NY.]: Cambridge University Press, ISBN 0-521-55001-7 : volume 1.
- ^ Zeeman, Erik Christopher (1964), "Causality implies the Lorentz group", Journal of Mathematical Physics 5 (4): 490–493, Bibcode 1964JMP.....5..490Z, doi:10.1063/1.1704140
- ^ Stauffer, Dietrich; Stanley, Harry Eugene (1995). From Newton to Mandelbrot: A Primer in Theoretical Physics (2nd enlarged ed.). Springer-Verlag. p. 80,81. ISBN 978-3540591917. http://books.google.com/books?id=o8rvAAAAMAAJ.
- ^ Einstein, Albert (1916). "Relativity: The Special and General Theory" (PDF). http://web.mit.edu/birge/Public/books/Einstein-Relativity.pdf. Retrieved 2008-11-01.
- ^ Wang Zhong-Yue, Wang Pin-Yu, Xu Yan-Rong (2011). "Crucial experiment to resolve Abraham-Minkowski Controversy". Optik 122 (22): 1994–1996. doi:10.1016/j.ijleo.2010.12.018.
Further reading
- Einstein, Albert (1961), Relativity: The Special and the General Theory, New York: Three Rivers Press (published 1995), ISBN 0-517-88441-0, http://www.marxists.org/reference/archive/einstein/works/1910s/relative/
- Ernst, A.; Hsu, J.-P. (2001), "First proposal of the universal speed of light by Voigt 1887", Chinese Journal of Physics 39 (3): 211–230, Bibcode 2001ChJPh..39..211E, http://psroc.phys.ntu.edu.tw/cjp/v39/211.pdf
- Thornton, Stephen T.; Marion, Jerry B. (2004), Classical dynamics of particles and systems (5th ed.), Belmont, [CA.]: Brooks/Cole, pp. 546–579, ISBN 0-534-40896-6
- Voigt, Woldemar (1887), "Über das Doppler'sche princip", Nachrichten von der Königlicher Gesellschaft den Wissenschaft zu Göttingen 2: 41–51
External links
- Derivation of the Lorentz transformations. This web page contains a more detailed derivation of the Lorentz transformation with special emphasis on group properties.
- The Paradox of Special Relativity. This webpage poses a problem, the solution of which is the Lorentz transformation, which is presented graphically in its next page.
- Relativity - a chapter from an online textbook
- Special Relativity: The Lorentz Transformation, The Velocity Addition Law on Project PHYSNET
- Warp Special Relativity Simulator. A computer program demonstrating the Lorentz transformations on everyday objects.
- Animation clip visualizing the Lorentz transformation.
- Lorentz Frames Animated from John de Pillis. Online Flash animations of Galilean and Lorentz frames, various paradoxes, EM wave phenomena, etc.
Categories:- Equations
- Minkowski spacetime
- Special relativity
- Fundamental physics concepts
- Functions and mappings
- Time
Wikimedia Foundation. 2010.









![L(\mathbf{u},U)L(\mathbf{u},V)=L(\mathbf{u}\oplus U\mathbf{v}, \mathrm{gyr}[\mathbf{u},U\mathbf{v}]UV)](0/430290ba85330e4703c555a67278d9b0.png)





![\phi = \ln \left[\gamma(1+\beta)\right] = -\ln \left[\gamma(1-\beta)\right] \,](5/4059316ea27f6c51c310306cc1753299.png)
















































