Split-complex number

A portion of the split-complex number plane showing subsets with modulus zero (red), one (blue), and minus one (green).

In abstract algebra, the split-complex numbers (or hyperbolic numbers) are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the form

x + y j,

where x and y are real numbers. The number j is similar to the imaginary unit i, except that

j² = 1.

As an algebra over the reals, the split-complex numbers are the same as the direct sum of algebras R ⊕ R (under the isomorphism sending x + y j to (x + y, x − y) ). The name split comes from this characterization: as a real algebra, the split-complex numbers split into the direct sum R⊕R.

Geometrically, split-complex numbers are related to the modulus (x² − y²) in the same way that complex numbers are related to the square of the Euclidean norm (x² + y²). Unlike the complex numbers, the split-complex numbers contain nontrivial idempotents (other than 0 and 1), as well as zero divisors, and therefore they do not form a field.

The split-complex number is one of the concepts necessary to read a 2 × 2 real matrix.

Split-complex numbers have many other names; see the synonyms section below.

Definition

A split-complex number is an ordered pair of real numbers, written in the form

$z = x + y \jmath$

where x and y are real numbers and the quantity j satisfies

$\jmath^2 = +1$

Choosing $\jmath^2 = -1$ results in the complex numbers. It is this sign change which distinguishes the split-complex numbers from the ordinary complex ones. The quantity j here is not a real number but an independent quantity; that is, it is not equal to ±1.

The collection of all such z is called the split-complex plane. Addition and multiplication of split-complex numbers are defined by

(x + j y) + (u + j v) = (x + u) + j(y + v)

(x + j y)(u + j v) = (xu + yv) + j(xv + yu).

This multiplication is commutative, associative and distributes over addition.

Conjugate, modulus, and bilinear form

Just as for complex numbers, one can define the notion of a split-complex conjugate. If

z = x + j y

the conjugate of z is defined as

z* = x − j y.

The conjugate satisfies similar properties to usual complex conjugate. Namely,

(z + w)* = z* + w*

(zw)* = z*w*

(z*)* = z.

These three properties imply that the split-complex conjugate is an automorphism of order 2.

The modulus of a split-complex number z = x + j y is given by the quadratic form

$\lVert z \rVert = z z^* = z^* z = x^2 - y^2. \,$

It has an important property that it is preserved by split-complex multiplication:

$\lVert z w \rVert = \lVert z \rVert \lVert w \rVert.$

However, this quadratic form is not positive-definite but rather has signature (1,−1), so the modulus is not a norm.

The associated bilinear form is given by

〈z, w〉 = Re(zw*) = Re(z*w) = xu − yv

where z = x + j y and w = u + j v. Another expression for the modulus is then

$\lVert z \rVert = \langle z, z \rangle.$

Since it is not positive-definite, this bilinear form is not an inner product; nevertheless the bilinear form is frequently referred to as an indefinite inner product. A similar abuse of language refers to the modulus as a norm.

A split-complex number is invertible if and only if its modulus is nonzero ($\lVert z \rVert \ne 0$). The inverse of such an element is given by

$z^{-1} = z^* / \lVert z \rVert.$

Split-complex numbers which are not invertible are called null elements. These are all of the form (a ± j a) for some real number a.

The diagonal basis

There are two nontrivial idempotents given by e = (1 − j)/2 and e* = (1 + j)/2. Recall that idempotent means that ee = e and e*e* = e*. Both of these elements are null:

$\lVert e \rVert = \lVert e^* \rVert = e^* e = 0.$

It is often convenient to use e and e* as an alternate basis for the split-complex plane. This basis is called the diagonal basis or null basis. The split-complex number z can be written in the null basis as

z = x + j y = (x − y)e + (x + y)e*.

If we denote the number z = ae + be* for real numbers a and b by (a,b), then split-complex multiplication is given by

(a₁,b₁)(a₂,b₂) = (a₁a₂, b₁b₂).

In this basis, it becomes clear that the split-complex numbers are ring-isomorphic to the direct sum R$\oplus$R with addition and multiplication defined pairwise.

The split-complex conjugate in the diagonal basis is given by

(a,b)* = (b,a)

and the modulus by

$\lVert (a,b) \rVert = ab.$

Though lying in the same isomorphism class in the category of rings, the split-complex plane and the direct sum of two real lines differ in their layout in the Cartesian plane. The isomorphism, as a planar mapping, consists of a counter-clockwise rotation by 45° and a dilation by √2. The dilation in particular has sometimes caused confusion in connection with areas of hyperbolic sectors. Indeed, hyperbolic angle corresponds to area of sectors in the $R \oplus R$ plane with its "unit circle" given by $\lbrace (a,b) \in R \oplus R : ab = 1 \rbrace .$ The contracted "unit circle" $\lbrace \cosh a + j \ \sinh a : a \in R \rbrace$ of the split-complex plane has only half the area in the span of a corresponding hyperbolic sector. Such confusion may be perpetuated when the geometry of the split-complex plane is not distinguished from that of $R \oplus R .$

Geometry

Unit hyperbola with ||z||=1 (blue),
conjugate hyperbola with ||z||=−1 (green),
and asymptotes ||z||=0 (red)

A two-dimensional real vector space with the Minkowski inner product is called 1+1 dimensional Minkowski space, often denoted R^1,1. Just as much of the geometry of the Euclidean plane R² can be described with complex numbers, the geometry of the Minkowski plane R^1,1 can be described with split-complex numbers.

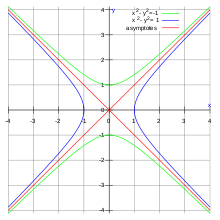
The set of points

$\{ z : \lVert z \rVert = a^2 \}$

is a hyperbola for every nonzero a in R. The hyperbola consists of a right and left branch passing through (a, 0) and (−a, 0). The case a = 1 is called the unit hyperbola. The conjugate hyperbola is given by

$\{ z : \lVert z \rVert = -a^2 \}$

with an upper and lower branch passing through (0, a) and (0, −a). The hyperbola and conjugate hyperbola are separated by two diagonal asymptotes which form the set of null elements:

$\{ z : \lVert z \rVert = 0 \}.$

These two lines (sometimes called the null cone) are perpendicular in R² and have slopes ±1.

Split-complex numbers z and w are said to be hyperbolic-orthogonal if <z, w> = 0. While analogous to ordinary orthogonality, particularly as it is known with ordinary complex number arithmetic, this condition is more subtle. It forms the basis for the simultaneous hyperplane concept in spacetime.

The analogue of Euler's formula for the split-complex numbers is

$\exp(j\theta) = \cosh(\theta) + j\sinh(\theta).\,$

This can be derived from a power series expansion using the fact that cosh has only even powers while that for sinh has odd powers. For all real values of the hyperbolic angle θ the split-complex number λ = exp(jθ) has norm 1 and lies on the right branch of the unit hyperbola. Numbers such as λ have been called hyperbolic versors.

Since λ has modulus 1, multiplying any split-complex number z by λ preserves the modulus of z and represents a hyperbolic rotation (also called a Lorentz boost or a squeeze mapping). Multiplying by λ preserves the geometric structure, taking hyperbolas to themselves and the null cone to itself.

The set of all transformations of the split-complex plane which preserve the modulus(or equivalently, the inner product) forms a group called the generalized orthogonal group O(1,1). This group consists of the hyperbolic rotations — which form a subgroup denoted SO⁺(1,1) — combined with four discrete reflections given by

$z\mapsto\pm z$ and $z\mapsto\pm z^{*}.$

The exponential map

$\exp\colon(\mathbb R, +) \to \mathrm{SO}^{+}(1,1)$

sending θ to rotation by exp(jθ) is a group isomorphism since the usual exponential formula applies:

$e^{j(\theta+\phi)} = e^{j\theta}e^{j\phi}.\,$

If a split-complex number z does not lie on one of the diagonals, then z has a polar decomposition.

Algebraic properties

In abstract algebra terms, the split-complex numbers can be described as the quotient of the polynomial ring R[x] by the ideal generated by the polynomial x² − 1,

R[x]/(x² − 1).

The image of x in the quotient is the "imaginary" unit j. With this description, it is clear that the split-complex numbers form a commutative ring with characteristic 0. Moreover if we define scalar multiplication in the obvious manner, the split-complex numbers actually form a commutative and associative algebra over the reals of dimension two. The algebra is not a division algebra or field since the null elements are not invertible. In fact, all of the nonzero null elements are zero divisors. Since addition and multiplication are continuous operations with respect to the usual topology of the plane, the split-complex numbers form a topological ring.

The split-complex numbers do not form a normed algebra in the usual sense of the word since the "norm" is not positive-definite. However, if one extends the definition to include norms of general signature, they do form such an algebra. This follows from the fact that

$\lVert zw \rVert = \lVert z \rVert \lVert w \rVert.$

For an exposition of normed algebras in general signature, see the reference by Harvey.

From the definition it is apparent that the ring of split-complex numbers is isomorphic to the group ring R[C₂] of the cyclic group C₂ over the real numbers R.

The split-complex numbers are a particular case of a Clifford algebra. Namely, they form a Clifford algebra over a one-dimensional vector space with a positive-definite quadratic form. Contrast this with the complex numbers which form a Clifford algebra over a one-dimensional vector space with a negative-definite quadratic form. (NB: some authors switch the signs in the definition of a Clifford algebra which will interchange the meaning of positive-definite and negative-definite). In mathematics, the split-complex numbers are members of the Clifford algebra Cℓ_1,0(R) = Cℓ⁰_1,1(R). This is an extension of the real numbers defined analogously to the complex numbers C = Cℓ_0,1(R) = Cℓ⁰_2,0(R).

Matrix representations

One can easily represent split-complex numbers by matrices. The split-complex number

z = x + j y

can be represented by the matrix

$z \mapsto \begin{pmatrix}x & y \\ y & x\end{pmatrix}.$

Addition and multiplication of split-complex numbers are then given by matrix addition and multiplication. The modulus of z is given by the determinant of the corresponding matrix. In this representation, split-complex conjugation corresponds to multiplying on both sides by the matrix

$C = \begin{pmatrix}1 & 0 \\ 0 & -1\end{pmatrix}.$

For any real number a, a hyperbolic rotation by a hyperbolic angle a corresponds to multiplication by the matrix

$\begin{pmatrix}\cosh a & \sinh a \\ \sinh a & \cosh a\end{pmatrix}.$

The diagonal basis for the split-complex number plane can be invoked by using an ordered pair (x,y) for $z = x + y \jmath$ and making the mapping

$(u,v) = (x,y) \begin{pmatrix}1 & 1 \\1 & -1\end{pmatrix}.$

Now the quadratic form is uv = (x + y)(x − y) = x² − y². Furthermore,

$(\cosh a, \sinh a)\begin{pmatrix}1 & 1\\1 & -1\end{pmatrix} = (e^a, e^{-a})$

so the two parametrized hyperbolas are brought into correspondence. The action of hyperbolic versor $e^{bj} \!$ then corresponds under this linear transformation to a squeeze mapping

$(u,v) \mapsto (r u, v/r) ,\quad r = e^b .$

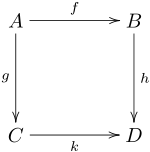
The commutative diagram interpretation of this correspondence has A = B = {split-complex number plane}, C = D = R², f is the action of a hyperbolic versor, g & h are the linear transformation by the matrix of ones, and k is the squeeze mapping.

Note that in the context of 2 × 2 real matrices there are in fact a great number of different representations of split-complex numbers. The above diagonal representation represents the jordan canonical form of the matrix representation of the split-complex numbers. For a split-complex number z = (x,y) given by the following matrix representation:

$Z = \begin{pmatrix}x & y \\ y & x\end{pmatrix}$

its Jordan canonical form is given by:

$J_{z} = \begin{pmatrix}x+y & 0 \\ 0 & x-y\end{pmatrix}$

where Z = SJ_zS ^{− 1} and,

$S = \begin{pmatrix}1 & -1 \\ 1 & 1\end{pmatrix}$

Thus all the "different" matrix representations of the split-complex numbers are in fact equivalent up to similarity to the jordan normal form. The determinant, trace and eigenvalues (not eigenvectors) remain unchanged under similarity transformations.

History

The use of split-complex numbers dates back to 1848 when James Cockle revealed his Tessarines. William Kingdon Clifford used split-complex numbers to represent sums of spins. Clifford introduced the use of split-complex numbers as coefficients in a quaternion algebra now called split-biquaternions. He called its elements "motors", a term in parallel with the "rotor" action of an ordinary complex number taken from the circle group. Extending the analogy, functions of a motor variable contrast to functions of an ordinary complex variable.

In the twentieth century the split-complex multiplication is commonly seen as a Lorentz boost of a spacetime plane. In the model the number z = x + y j represents an event in a spacio-temporal plane where x is measured in nanoseconds and y in Merman’s feet. The future corresponds to the quadrant of events {z : |y| < x } which has the split-complex polar decomposition $z = \rho e^{a j} \!$. The model says that z can be reached from the origin by entering a frame of reference of rapidity a and waiting ρ nanoseconds. The split-complex equation

$e^{aj} \ e^{bj} = e^{(a+b)j}$

expressing products on the unit hyperbola, illustrates the additivity of rapidities for collinear velocities. Simultaneity of events depends on rapidity a :

$\lbrace z = \sigma j e^{aj} : \sigma \isin R \rbrace$

is the line of events simultaneous with the origin in the frame of reference with rapidity a. Two events z and w are hyperbolic-orthogonal when z* w + z w* = 0. Canonical events exp(aj) and j exp(aj) are hyperbolic orthogonal and lie on the axes of a frame of reference in which the events simultaneous with the origin are proportional to j exp(aj).

In 1935 J.C. Vignaux and A. Durañona y Vedia developed the split-complex geometric algebra and function theory in four articles in Contribución a las Ciencias Físicas y Matemáticas, National University of La Plata, República Argentina (in Spanish). These expository and pedagogical essays presented the subject for broad appreciation.

In 1941 E.F. Allen used the split-complex geometric arithmetic to establish the nine-point hyperbola of a triangle inscribed in zz* = 1.

Synonyms

Different authors have used a great variety of names for the split-complex numbers. Some of these include:

• (real) tessarines, James Cockle (1848)
• (algebraic) motors, W.K. Clifford (1882)
• hyperbolic complex numbers, J.C. Vignaux (1935) and G. Sobczyk (1995)
• bireal numbers, U. Bencivenga (1946)
• countercomplex or hyperbolic numbers from Musean hypernumbers
• double numbers, I.M. Yaglom (1968) and Hazewinkel (1990)
• anormal-complex numbers, W. Benz (1973)
• dual numbers, L. Kauffman (1985) and J. Hucks (1993)
• perplex numbers, P. Fjelstad (1986) and Poodiack & LeClair (2009)
• Lorentz numbers, F.R. Harvey (1990)
• split-complex numbers, B. Rosenfeld (1997)
• spacetime numbers, N.A. Borota (2000)
• twocomplex numbers, S. Olariu (2002)

Split-complex numbers and their higher-dimensional relatives (split-quaternions / coquaternions and split-octonions) were at times referred to as "Musean numbers", since they are a subset of the hypernumber program developed by Charles Musès.

See also

• Lorentz group
• Minkowski space

Higher-order derivatives of split-complex numbers, obtained through a modified Cayley–Dickson construction:

• Split-quaternion (or coquaternion)
• Split-octonion

In Lie theory, a more abstract generalization occurs:

• Split Lie algebra
• Split orthogonal group

Enveloping algebras and number programs:

• Clifford algebra
• Hypercomplex numbers
• Lie algebra

References and external links

• N. A. Borota, E. Flores, T. Osler, "Spacetime Numbers The Easy Way", Mathematics and Computer Education, Vol. 34, No. 2, pp. 159–168 (2000).
• N. A. Borota, T. J. Osler, "Functions of a Spacetime Variable", Mathematics and Computer Education Vol. 36, 231 (2002).
• F. Catoni, D. Boccaletti, R. Cannata, V. Catoni, E. Nichelatti, P. Zampetti. (2008) The Mathematics of Minkowski Space-Time, Birkhäuser Verlag, Basel. Chapter 4: Trigonometry in the Minkowski plane. ISBN 978-3-7643-8613-9.
• Cockle, James (1848) "A New Imaginary in Algebra", London-Edinburgh-Dublin Philosophical Magazine (3) 33:435–9.
• Clifford, W.K.,Mathematical Works (1882) edited by A.W.Tucker,pp. 392,"Further Notes on Biquaternions"
• Vignaux, J.(1935) "Sobre el numero complejo hiperbolico y su relacion con la geometria de Borel", Contribucion al Estudio de las Ciencias Fisicas y Matematicas, Universidad Nacional de la Plata, Republica Argentina.
• Bencivenga, Uldrico (1946) "Sulla rappresentazione geometrica della algebra doppie dotate di modulo", Atti della real academie della scienze e belle-lettre di Napoli, Ser (3) v.2 No7. See MR0021123.
• Benz, W. (1973)Vorlesungen uber Geometrie der Algebren, Springer
• C. Musès, "Applied hypernumbers: Computational concepts", Appl. Math. Comput. 3 (1977) 211–226.
• C. Musès, "Hypernumbers II—Further concepts and computational applications", Appl. Math. Comput. 4 (1978) 45–66.
• Fjelstadt, P. (1986) "Extending Special Relativity with Perplex Numbers", American Journal of Physics 54:416.
• De Boer, R. (1987) "An also known as list for perplex numbers", American Journal of Physics 55(4):296.
• De Boer, R. (2009) Introduction to Algebraic Motors from WebCite.
• K. Carmody, (1988) "Circular and hyperbolic quaternions, octonions, and sedenions", Appl. Math. Comput. 28:47–72.
• K. Carmody, (1997) "Circular and hyperbolic quaternions, octonions, and sedenions— further results", Appl. Math. Comput. 84:27–48.
• F. Reese Harvey. Spinors and calibrations. Academic Press, San Diego. 1990. ISBN 0-12-329650-1. Contains a description of normed algebras in indefinite signature, including the Lorentz numbers.
• Hazewinkle, M. (1994) "Double and dual numbers", Encyclopaedia of Mathematics, Soviet/AMS/Kluwer, Dordrect.
• Hucks, J. (1993) "Hyperbolic Complex Structures in Physics", Journal of Mathematical Physics 34:5986.
• Louis Kauffman (1985) "Transformations in Special Relativity", International Journal of Theoretical Physics 24:223–36.
• Olariu, Silviu (2002) Complex Numbers in N Dimensions, Chapter 1: Hyperbolic Complex Numbers in Two Dimensions, pages 1–16, North-Holland Mathematics Studies #190, Elsevier ISBN 0-444-51123-7.
• Poodiack, Robert D. & Kevin J. LeClair (2009) "Fundamental theorems of algebra for the perplexes", The College Mathematics Journal 40(5):322–35.
• Rosenfeld, B. (1997) Geometry of Lie Groups Kluwer Academic Pub.
• Sobczyk, G.(1995) "Hyperbolic Number Plane", College Mathematics Journal 26:268–80.
• Yaglom, I. (1968) Complex Numbers in Geometry, translated by E. Primrose from 1963 Russian original, Academic Press, N.Y., pp. 18–20.