- Commutative diagram
-
For help on drawing commutative diagrams on Wikipedia, see meta:Help:Displaying a formula#Commutative_diagrams.
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects (also known as vertices) and morphisms (also known as arrows or edges) such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition. Commutative diagrams play the role in category theory that equations play in algebra.
Note that a diagram may not be commutative, i.e. the composition of different paths in the diagram may not give the same result. For clarification, phrases like "this commutative diagram" or "the diagram commutes" may be used.
Contents
Examples
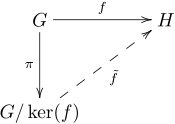
In the following diagram expressing the first isomorphism theorem, commutativity means that
 :
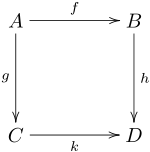
:Below is a generic commutative square, in which

Symbols
In algebra texts, the type of morphism can be denoted with different arrow usages: monomorphisms with a
 , epimorphisms with a
, epimorphisms with a  , and isomorphisms with a
, and isomorphisms with a  . The dashed arrow typically represents the claim that the indicated morphism exists whenever the rest of the diagram holds. This is common enough that texts often do not explain the meanings of the different types of arrow.
. The dashed arrow typically represents the claim that the indicated morphism exists whenever the rest of the diagram holds. This is common enough that texts often do not explain the meanings of the different types of arrow.Verifying commutativity
Commutativity makes sense for a polygon of any finite number of sides (including just 1 or 2), and a diagram is commutative if every polygonal subdiagram is commutative.
Diagram chasing
Diagram chasing is a method of mathematical proof used especially in homological algebra. Given a commutative diagram, a proof by diagram chasing involves the formal use of the properties of the diagram, such as injective or surjective maps, or exact sequences. A syllogism is constructed, for which the graphical display of the diagram is just a visual aid. It follows that one ends up "chasing" elements around the diagram, until the desired element or result is constructed or verified.
Examples of proofs by diagram chasing include those typically given for the five lemma, the snake lemma, the zig-zag lemma, and the nine lemma.
Diagrams as functors
A commutative diagram in a category C can be interpreted as a functor from an index category J to C; one calls the functor a diagram.
More formally, a commutative diagram is a visualization of a diagram indexed by a poset category:
- one draws a node for every object in the index category,
- an arrow for a generating set of morphisms,
- omitting identity maps and morphisms that can be expressed as compositions,
- and the commutativity of the diagram (the equality of different compositions of maps between two objects) corresponds to the uniqueness of a map between two objects in a poset category.
Conversely, given a commutative diagram, it defines a poset category:
- the objects are the nodes,
- there is a morphism between any two objects if and only if there is a (directed) path between the nodes,
- with the relation that this morphism is unique (any composition of maps is defined by its domain and target: this is the commutativity axiom).
However, not every diagram commutes (the notion of diagram strictly generalizes commutative diagram): most simply, the diagram of a single object with an endomorphism (
 ), or with two parallel arrows (
), or with two parallel arrows ( ;
;  ), as used in the definition of equalizer need not commute. Further, diagrams may be messy or impossible to draw when the number of objects or morphisms is large (or even infinite).
), as used in the definition of equalizer need not commute. Further, diagrams may be messy or impossible to draw when the number of objects or morphisms is large (or even infinite).See also
External links
Categories:- Homological algebra
- Category theory
- Proofs
- Mathematical terminology
- Diagrams
Wikimedia Foundation. 2010.