Basis (linear algebra)

Basis vector redirects here. For basis vector in the context of crystals, see crystal structure. For a more general concept in physics, see frame of reference.

In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system".^[1] In more general terms, a basis is a linearly independent spanning set.

Given a basis of vector space, every element of the vector space can be expressed uniquely as a finite linear combination of basis vectors. Every vector space has a basis, and all bases of a vector space have the same number of elements, called the dimension of the vector space.

Definition

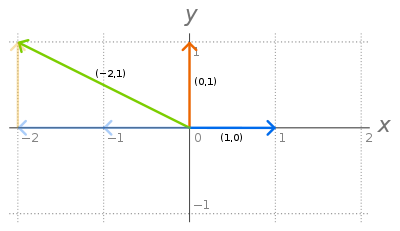This picture illustrates the standard basis in R². The blue and orange vectors are the elements of the basis; the green vector can be given in terms of the basis vectors, and so is linearly dependent upon them.

A basis B of a vector space V over a field F is a linearly independent subset of V that spans (or generates) V.

In more detail, suppose that B = { v₁, …, v_n } is a finite subset of a vector space V over a field F (such as the real or complex numbers R or C). Then B is a basis if it satisfies the following conditions:

• the linear independence property,

for all a₁, …, a_n ∈ F, if a₁v₁ + … + a_nv_n = 0, then necessarily a₁ = … = a_n = 0; and

• the spanning property,

for every x in V it is possible to choose a₁, …, a_n ∈ F such that x = a₁v₁ + … + a_nv_n.

The numbers a_i are called the coordinates of the vector x with respect to the basis B, and by the first property they are uniquely determined.

A vector space that has a finite basis is called finite-dimensional. To deal with infinite-dimensional spaces, we must generalize the above definition to include infinite basis sets. We therefore say that a set (finite or infinite) B ⊂ V is a basis, if

• every finite subset B₀ ⊆ B obeys the independence property shown above; and
• for every x in V it is possible to choose a₁, …, a_n ∈ F and v₁, …, v_n ∈ B such that x = a₁v₁ + … + a_nv_n.

The sums in the above definition are all finite because without additional structure the axioms of a vector space do not permit us to meaningfully speak about an infinite sum of vectors. Settings that permit infinite linear combinations allow alternative definitions of the basis concept: see Related notions below.

It is often convenient to list the basis vectors in a specific order, for example, when considering the transformation matrix of a linear map with respect to a basis. We then speak of an ordered basis, which we define to be a sequence (rather than a set) of linearly independent vectors that span V: see Ordered bases and coordinates below.

Expression of a basis

Basis defined by Euler angles - The xyz (fixed) system is shown in blue, the XYZ (rotated) system is shown in red. The line of nodes, labeled N, is shown in green.

There are several ways to describe a basis for the space. Some are made ad-hoc for a specific dimension. For example, there are several ways to give a basis in dim 3, like Euler angles.

The general case is to give a matrix with the components of the new basis vectors in columns. This is also the more general method because it can express any possible set of vectors even if it is not a basis. This matrix can be seen as three things:

Basis Matrix: Is a matrix that represents the basis, because its columns are the components of vectors of the basis. This matrix represents any vector of the new basis as linear combination of the current basis.

Rotation operator: When orthonormal bases are used, any other orthonormal basis can be defined by a rotation matrix. This matrix represents the rotation operator that rotates the vectors of the basis to the new one. It is exactly the same matrix as before because the rotation matrix multiplied by the identity matrix I has to be the new basis matrix.

Change of basis matrix: This matrix can be used to change different objects of the space to the new basis. Therefore is called "change of basis" matrix. It is important to note that some objects change their components with this matrix and some others, like vectors, with its inverse.

Properties

Again, B denotes a subset of a vector space V. Then, B is a basis if and only if any of the following equivalent conditions are met:

• B is a minimal generating set of V, i.e., it is a generating set and no proper subset of B is also a generating set.
• B is a maximal set of linearly independent vectors, i.e., it is a linearly independent set but no other linearly independent set contains it as a proper subset.
• Every vector in V can be expressed as a linear combination of vectors in B in a unique way. If the basis is ordered (see Ordered bases and coordinates below) then the coefficients in this linear combination provide coordinates of the vector relative to the basis.

Every vector space has a basis. The proof of this requires the axiom of choice. All bases of a vector space have the same cardinality (number of elements), called the dimension of the vector space. This result is known as the dimension theorem, and requires the ultrafilter lemma, a strictly weaker form of the axiom of choice.

Also many vector sets can be attributed a standard basis which comprises both spanning and linearly independent vectors.

Standard bases for example:

In Rⁿ {E1,...,En} where En is the n-th column of the identity matrix which consists of all ones in the main diagonal and zeros everywhere else. This is because the columns of the identity matrix are linearly independent can always span a vector set by expressing it as a linear combination.

In P₂ where P₂ is the set of all polynomials of degree at most 2 {1,x,x²} is the standard basis.

In M₂₂ {M_1,1,M_1,2,M_2,1,M_2,2} where M₂₂ is the set of all 2x2 matrices. and M_m,n is the 2x2 matrix with a 1 in the m,n position and zeros everywhere else. This again is a standard basis since it is linearly independent and spanning.

Examples

• Consider R², the vector space of all coordinates (a, b) where both a and b are real numbers. Then a very natural and simple basis is simply the vectors e₁ = (1,0) and e₂ = (0,1): suppose that v = (a, b) is a vector in R², then v = a (1,0) + b (0,1). But any two linearly independent vectors, like (1,1) and (−1,2), will also form a basis of R² (see the section Proving that a finite spanning set is a basis^{[dead link]} further down).

• More generally, the vectors e₁, e₂, ..., e_n are linearly independent and generate Rⁿ. Therefore, they form a basis for Rⁿ and the dimension of Rⁿ is n. This basis is called the standard basis.

• Let V be the real vector space generated by the functions e^t and e^2t. These two functions are linearly independent, so they form a basis for V.

• Let R[x] denote the vector space of real polynomials; then (1, x, x², ...) is a basis of R[x]. The dimension of R[x] is therefore equal to aleph-0.

Extending to a basis

Let S be a subset of a vector space V. To extend S to a basis means to find a basis B that contains S as a subset. This can be done if and only if S is linearly independent. Almost always, there is more than one such B, except in rather special circumstances (i.e. L is already a basis, or L is empty and V has two elements).

A similar question is when does a subset S contain a basis. This occurs if and only if S spans V. In this case, S will usually contain several different bases.

Example of alternative proofs

Often, a mathematical result can be proven in more than one way. Here, using three different proofs, we show that the vectors (1,1) and (−1,2) form a basis for R².

From the definition of basis

We have to prove that these two vectors are linearly independent and that they generate R².

Part I: If two vectors v,w are linearly independent, then av + bw = 0 (a and b scalars) implies a = 0,b = 0.

To prove that they are linearly independent, suppose that there are numbers a,b such that:

$a(1,1)+b(-1,2)=(0,0). \,$

(i.e., they are linearly dependent) Then:

$(a-b,a+2b)=(0,0) \,$

  and  

$a-b=0 \;$

  and  

$a+2b=0. \,$

Subtracting the first equation from the second, we obtain:

$3b=0 \;$

  so  

$b=0. \,$

Subtracting this equation from the first equation then:

$a=0. \,$

Hence we have linear independence.

Part II: To prove that these two vectors generate R², we have to let (a,b) be an arbitrary element of R², and show that there exist numbers r,s ∈ R such that:

$r(1,1)+s(-1,2)=(a,b). \,$

Then we have to solve the equations:

$r-s=a \,$

$r+2s=b. \,$

Subtracting the first equation from the second, we get:

$3s=b-a, \,$

          and then

$s=(b-a)/3, \,$

        and finally

$r=s+a=((b-a)/3)+a=(b+2a)/3. \,$

By the dimension theorem

Since (−1,2) is clearly not a multiple of (1,1) and since (1,1) is not the zero vector, these two vectors are linearly independent. Since the dimension of R² is 2, the two vectors already form a basis of R² without needing any extension.

By the invertible matrix theorem

Simply compute the determinant

$\det\begin{bmatrix}1&-1\\1&2\end{bmatrix}=3\neq0.$

Since the above matrix has a nonzero determinant, its columns form a basis of R². See: invertible matrix.

Ordered bases and coordinates

A basis is just a set of vectors with no given ordering. For many purposes it is convenient to work with an ordered basis. For example, when working with a coordinate representation of a vector it is customary to speak of the "first" or "second" coordinate, which makes sense only if an ordering is specified for the basis. For finite-dimensional vector spaces one typically indexes a basis {v_i} by the first n integers. An ordered basis is also called a frame.

Suppose V is an n-dimensional vector space over a field F. A choice of an ordered basis for V is equivalent to a choice of a linear isomorphism φ from the coordinate space Fⁿ to V.

Proof. The proof makes use of the fact that the standard basis of Fⁿ is an ordered basis.

Suppose first that

φ : Fⁿ → V

is a linear isomorphism. Define an ordered basis {v_i} for V by

v_i = φ(e_i) for 1 ≤ i ≤ n

where {e_i} is the standard basis for Fⁿ.

Conversely, given an ordered basis, consider the map defined by

φ(x) = x₁v₁ + x₂v₂ + ... + x_nv_n,

where x = x₁e₁ + x₂e₂ + ... + x_ne_n is an element of Fⁿ. It is not hard to check that φ is a linear isomorphism.

These two constructions are clearly inverse to each other. Thus ordered bases for V are in 1-1 correspondence with linear isomorphisms Fⁿ → V.

The inverse of the linear isomorphism φ determined by an ordered basis {v_i} equips V with coordinates: if, for a vector v ∈ V, φ⁻¹(v) = (a₁, a₂,...,a_n) ∈ Fⁿ, then the components a_j = a_j(v) are the coordinates of v in the sense that v = a₁(v) v₁ + a₂(v) v₂ + ... + a_n(v) v_n.

The maps sending a vector v to the components a_j(v) are linear maps from V to F, because of φ⁻¹ is linear. Hence they are linear functionals. They form a basis for the dual space of V, called the dual basis.

Related notions

Analysis

In the context of infinite-dimensional vector spaces over the real or complex numbers, the term Hamel basis (named after Georg Hamel) or algebraic basis can be used to refer to a basis as defined in this article. This is to make a distinction with other notions of "basis" that exist when infinite-dimensional vector spaces are endowed with extra structure. The most important alternatives are orthogonal bases on Hilbert spaces, Schauder bases and Markushevich bases on normed linear spaces.

The common feature of the other notions is that they permit the taking of infinite linear combinations of the basic vectors in order to generate the space. This, of course, requires that infinite sums are meaningfully defined on these spaces, as is the case for topological vector spaces – a large class of vector spaces including e.g. Hilbert spaces, Banach spaces or Fréchet spaces.

The preference of other types of bases for infinite dimensional spaces is justified by the fact that the Hamel basis becomes "too big" in Banach spaces: If X is an infinite dimensional normed vector space which is complete (i.e. X is a Banach space), then any Hamel basis of X is necessarily uncountable. This is a consequence of the Baire category theorem. The completeness as well as infinite dimension are crucial assumptions in the previous claim. Indeed, finite dimensional spaces have by definition finite basis and there are infinite dimensional (non-complete) normed spaces which have countable Hamel basis. Consider c₀₀, the space of the sequences x = (x_n) of real numbers which have only finitely many non-zero coordinates, with the norm $\|x\|=\sup_n |x_n|.$ The standard basis is its countable Hamel basis.

Example

In the study of Fourier series, one learns that the functions {1} ∪ { sin(nx), cos(nx) : n = 1, 2, 3, ... } are an "orthogonal basis" of the (real or complex) vector space of all (real or complex valued) functions on the interval [0, 2π] that are square-integrable on this interval, i.e., functions f satisfying

$\int_0^{2\pi} \left|f(x)\right|^2\,dx<\infty.$

The functions {1} ∪ { sin(nx), cos(nx) : n = 1, 2, 3, ... } are linearly independent, and every function f that is square-integrable on [0, 2π] is an "infinite linear combination" of them, in the sense that

$\lim_{n\rightarrow\infty}\int_0^{2\pi}\biggl|a_0+\sum_{k=1}^n \bigl(a_k\cos(kx)+b_k\sin(kx)\bigr)-f(x)\biggr|^2\,dx=0$

for suitable (real or complex) coefficients a_k, b_k. But most square-integrable functions cannot be represented as finite linear combinations of these basis functions, which therefore do not comprise a Hamel basis. Every Hamel basis of this space is much bigger than this merely countably infinite set of functions. Hamel bases of spaces of this kind are typically not useful, whereas orthonormal bases of these spaces are essential in Fourier analysis.

Affine geometry

The related notions of an affine space, projective space, convex set, and cone have related notions of affine basis^[2] (a basis for an n-dimensional affine space is n + 1 points in general linear position), projective basis (essentially the same as an affine basis, this is n + 1 points in general linear position, here in projective space), convex basis (the vertices of a polytope), and cone basis^[3] (points on the edges of a polygonal cone); see also a Hilbert basis (linear programming).

See also

• Change of basis

Notes

1. ^ Halmos, Paul Richard (1987) Finite-dimensional vector spaces (4th edition) Springer-Verlag, New York, page 10, ISBN 0-387-90093-4
2. ^ Notes on geometry, by Elmer G. Rees, p. 7
3. ^ Some remarks about additive functions on cones, Marek Kuczma

References

General references

• Blass, Andreas (1984), "Existence of bases implies the axiom of choice", Axiomatic set theory, Contemporary Mathematics volume 31, Providence, R.I.: American Mathematical Society, pp. 31–33, ISBN 0-8218-5026-1, MR763890 
• Brown, William A. (1991), Matrices and vector spaces, New York: M. Dekker, ISBN 978-0-8247-8419-5 
• Lang, Serge (1987), Linear algebra, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96412-6 

Historical references

• (French) Banach, Stefan (1922), "Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)", Fundamenta Mathematicae 3, ISSN 0016-2736, http://matwbn.icm.edu.pl/ksiazki/fm/fm3/fm3120.pdf 
• (German) Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry), http://dml.cz/handle/10338.dmlcz/400338 
• (French) Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics), Paris: Hermann 
• Dorier, Jean-Luc (1995), "A general outline of the genesis of vector space theory", Historia Mathematica 22 (3): 227–261, doi:10.1006/hmat.1995.1024, MR1347828, http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6WG9-45NJHDR-C&_user=1634520&_coverDate=12%2F31%2F1995&_rdoc=2&_fmt=high&_orig=browse&_srch=doc-info(%23toc%236817%231995%23999779996%23308480%23FLP%23display%23Volume)&_cdi=6817&_sort=d&_docanchor=&_ct=9&_acct=C000054038&_version=1&_urlVersion=0&_userid=1634520&md5=fd995fe2dd19abde0c081f1e989af006 
• (French) Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, http://books.google.com/books?id=TDQJAAAAIAAJ 
• (German) Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik, http://books.google.com/books?id=bKgAAAAAMAAJ&pg=PA1&dq=Die+Lineale+Ausdehnungslehre+ein+neuer+Zweig+der+Mathematik , reprint: Hermann Grassmann. Translated by Lloyd C. Kannenberg. (2000), Extension Theory, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2031-5 
• Hamilton, William Rowan (1853), Lectures on Quaternions, Royal Irish Academy, http://historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=05230001&seq=9 
• (German) Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry), http://mathdoc.emath.fr/cgi-bin/oeitem?id=OE_MOBIUS__1_1_0 
• Moore, Gregory H. (1995), "The axiomatization of linear algebra: 1875–1940", Historia Mathematica 22 (3): 262–303, doi:10.1006/hmat.1995.1025, http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6WG9-45NJHDR-D&_user=1634520&_coverDate=12%2F31%2F1995&_rdoc=3&_fmt=high&_orig=browse&_srch=doc-info(%23toc%236817%231995%23999779996%23308480%23FLP%23display%23Volume)&_cdi=6817&_sort=d&_docanchor=&_ct=9&_acct=C000054038&_version=1&_urlVersion=0&_userid=1634520&md5=4327258ef37b4c293b560238058e21ad 
• (Italian) Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva, Turin 

External links

• Instructional videos from Khan Academy
  • Introduction to bases of subspaces
  • Proof that any subspace basis has same number of elements