- Rotation matrix
-
In linear algebra, a rotation matrix is a matrix that is used to perform a rotation in Euclidean space. For example the matrix
rotates points in the xy-Cartesian plane counterclockwise through an angle θ about the origin of the Cartesian coordinate system. To perform the rotation using a rotation matrix R, the position of each point must be represented by a column vector v, containing the coordinates of the point. A rotated vector is obtained by using the matrix multiplication Rv. Since matrix multiplication always fixes the zero vector, rotation matrices can only be used to describe rotations that fix the origin.
Rotation matrices provide a simple algebraic description of such rotations, and are used extensively for computations in geometry, physics, and computer graphics. These rotations can be in dimension 2, where they are determined by the angle θ of rotation, or in dimension 3, where in addition an axis of rotation is involved; the angle and axis are implicitly represented by the entries of the rotation matrix. The notion of rotation is not commonly used in dimensions higher than 3; there is a notion of a rotational displacement, which can be represented by a matrix, but no associated single axis or angle.
Rotation matrices are square matrices, with real entries. More specifically they can be characterized as orthogonal matrices with determinant 1:
 .
.
The set of all such matrices of size n forms a group, known as the special orthogonal group SO(n).
Rotations in two dimensions
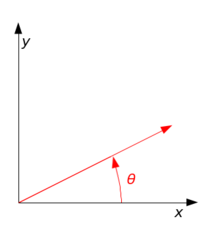
In two dimensions every rotation matrix has the following form:
 .
.
This rotates column vectors by means of the following matrix multiplication:
 .
.
So the coordinates (x',y') of the point (x,y) after rotation are:
 ,
, .
.
The direction of vector rotation is counterclockwise if θ is positive (e.g. 90°), and clockwise if θ is negative (e.g. -90°).
 .
.
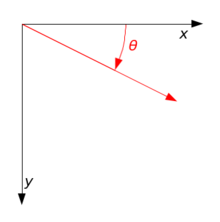
Non-standard orientation of the coordinate system
If a standard right-handed Cartesian coordinate system is used, with the x axis to the right and the y axis up, the rotation R(θ) is counterclockwise. If a left-handed Cartesian coordinate system is used, with x directed to the right but y directed down, R(θ) is clockwise. Such non-standard orientations are rarely used in mathematics but are common in 2D computer graphics, which often have the origin in the top left corner and the y-axis down the screen or page.[1]
See below for other alternative conventions which may change the sense of the rotation produced by a rotation matrix.
Common rotations
Particularly useful are the matrices for 90° and 180° rotations:
![R(90^\circ) = \begin{bmatrix}
0 & -1 \\[3pt]
1 & 0 \\
\end{bmatrix}](c/dbcfcdc115372dfe6e66982a841f9076.png) (90° counterclockwise rotation)
(90° counterclockwise rotation)![R(180^\circ) = \begin{bmatrix}
-1 & 0 \\[3pt]
0 & -1 \\
\end{bmatrix}](d/b0d7db5b1cf2e531126f13e1de38113b.png) (180° rotation in either direction – a half-turn)
(180° rotation in either direction – a half-turn)![R(270^\circ) = \begin{bmatrix}
0 & 1 \\[3pt]
-1 & 0 \\
\end{bmatrix}](7/e17c4efcf457f9c618c5642111d8bb46.png) (270° counterclockwise rotation, the same as a 90° clockwise rotation)
(270° counterclockwise rotation, the same as a 90° clockwise rotation)
Rotations in three dimensions
See also: Rotation representationBasic rotations
The following three basic (gimbal-like) rotation matrices rotate vectors about the x, y, or z axis, in three dimensions:
Each of these basic vector rotations typically appears counter-clockwise when the axis about which they occur points toward the observer, and the coordinate system is right-handed. Rz, for instance, would rotate toward the y-axis a vector aligned with the x-axis. This is similar to the rotation produced by the above mentioned 2-D rotation matrix. See below for alternative conventions which may apparently or actually invert the sense of the rotation produced by these matrices.
General rotations
Other rotation matrices can be obtained from these three using matrix multiplication. For example, the product
represents a rotation whose yaw, pitch, and roll are α, β, and γ, respectively. Similarly, the product
represents a rotation whose Euler angles are α, β, and γ (using the y-x-z convention for Euler angles).
The orthogonal matrix (post-multiplying a column vector) corresponding to a clockwise/left-handed rotation with Euler angles ϕ,θ,ψ, with x-y-z convention, is given by:
Conversion from and to axis-angle
Every rotation in three dimensions is defined by its axis — a direction that is left fixed by the rotation — and its angle — the amount of rotation about that axis (Euler rotation theorem).
There are several methods to compute an axis and an angle from a rotation matrix (see also axis-angle). Here, we only describe the method based on the computation of the eigenvectors and eigenvalues of the rotation matrix. It is also possible to use the trace of the rotation matrix.
Determining the axis
Given a rotation matrix R, a vector u parallel to the rotation axis must satisfy
since the rotation of
 around the rotation axis must result in
around the rotation axis must result in  . The equation above may be solved for
. The equation above may be solved for  which is unique up to a scalar factor.
which is unique up to a scalar factor.Further, the equation may be rewritten
which shows that
 is the null space of R − I. Viewed another way,
is the null space of R − I. Viewed another way,  is an eigenvector of R corresponding to the eigenvalue λ = 1 (every rotation matrix must have this eigenvalue).
is an eigenvector of R corresponding to the eigenvalue λ = 1 (every rotation matrix must have this eigenvalue).Determining the angle
To find the angle of a rotation, once the axis of the rotation is known, select a vector
 perpendicular to the axis. Then the angle of the rotation is the angle between
perpendicular to the axis. Then the angle of the rotation is the angle between  and
and  .
.A much easier method, however, is to calculate the trace (i.e. the sum of the diagonal elements of the rotation matrix) which is 1 + 2cos θ.
Rotation matrix from axis and angle
For some applications, it is helpful to be able to make a rotation with a given axis. Given a unit vector u = (ux, uy, uz), where ux2 + uy2 + uz2 = 1, the matrix for a rotation by an angle of θ about an axis in the direction of u is
This can be written more concisely as
where
![[\mathbf u]_{\times}](7/517ec53080ac79a8b3dc754a4a90ede4.png) is the cross product matrix of u, ⊗ is the tensor product and I is the Identity matrix. This is a matrix form of Rodrigues' rotation formula, with
is the cross product matrix of u, ⊗ is the tensor product and I is the Identity matrix. This is a matrix form of Rodrigues' rotation formula, withIf the 3D space is right-handed, this rotation will be counterclockwise for an observer placed so that the axis u goes in his or her direction (Right-hand rule).
Properties of a rotation matrix
In three dimensions, for any rotation matrix
 , where a is a rotation axis and θ a rotation angle,
, where a is a rotation axis and θ a rotation angle,-
 (i.e.,
(i.e.,  is an orthogonal matrix)
is an orthogonal matrix) (i.e, the determinant of
(i.e, the determinant of  is 1)
is 1)
 (where
(where  is the identity matrix)
is the identity matrix)- The eigenvalues of
 are
are
-
- where i is the standard imaginary unit with the property i2 = − 1
- The trace of
 is
is  equivalent to the sum of its eigenvalues.
equivalent to the sum of its eigenvalues.
Some of these properties can be generalised to any number of dimensions. In other words, they hold for any rotation matrix
 .
.For instance, in two dimensions the properties hold with the following exceptions:
-
- a is not a given axis, but a point (rotation center) which must coincide with the origin of the coordinate system in which the rotation is represented.
- Consequently, the four elements of the rotation matrix depend only on θ, hence we write
 , rather than
, rather than 
- The eigenvalues of
 are
are 
- The trace of
 is
is  equivalent to the sum of its eigenvalues.
equivalent to the sum of its eigenvalues.
Examples
- The 2×2 rotation matrix
- The transpose of the 2×2 matrix
- The 3×3 rotation matrix
- The 3×3 rotation matrix
- The 3×3 permutation matrix
- The 3×3 matrix
- The 4×3 matrix
- The 4×4 matrix
- The 5×5 rotation matrix
Geometry
In Euclidean geometry, a rotation is an example of an isometry, a transformation that moves points without changing the distances between them. Rotations are distinguished from other isometries by two additional properties: they leave (at least) one point fixed, and they leave "handedness" unchanged. By contrast, a translation moves every point, a reflection exchanges left- and right-handed ordering, and a glide reflection does both.
A rotation that does not leave "handedness" unchanged is an improper rotation or a rotoinversion.
If we take the fixed point as the origin of a Cartesian coordinate system, then every point can be given coordinates as a displacement from the origin. Thus we may work with the vector space of displacements instead of the points themselves. Now suppose (p1,…,pn) are the coordinates of the vector p from the origin, O, to point P. Choose an orthonormal basis for our coordinates; then the squared distance to P, by Pythagoras, is
which we can compute using the matrix multiplication
A geometric rotation transforms lines to lines, and preserves ratios of distances between points. From these properties we can show that a rotation is a linear transformation of the vectors, and thus can be written in matrix form, Qp. The fact that a rotation preserves, not just ratios, but distances themselves, we can state as
or
Because this equation holds for all vectors, p, we conclude that every rotation matrix, Q, satisfies the orthogonality condition,
Rotations preserve handedness because they cannot change the ordering of the axes, which implies the special matrix condition,
Equally important, we can show that any matrix satisfying these two conditions acts as a rotation.
Multiplication
The inverse of a rotation matrix is its transpose, which is also a rotation matrix:
The product of two rotation matrices is a rotation matrix:
For n greater than 2, multiplication of n×n rotation matrices is not commutative.
Noting that any identity matrix is a rotation matrix, and that matrix multiplication is associative, we may summarize all these properties by saying that the n×n rotation matrices form a group, which for n > 2 is non-abelian. Called a special orthogonal group, and denoted by SO(n), SO(n,R), SOn, or SOn(R), the group of n×n rotation matrices is isomorphic to the group of rotations in an n-dimensional space. This means that multiplication of rotation matrices corresponds to composition of rotations, applied in left-to-right order of their corresponding matrices.
Ambiguities
The interpretation of a rotation matrix can be subject to many ambiguities.
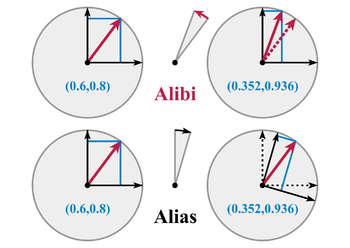
- Alias or alibi transformation
- The change in a vector's coordinates can be due to a turn of the coordinate system (alias) or a turn of the vector (alibi). Any rotation can be legitimately described both ways, as vectors and coordinate systems actually rotate with respect to each other. Throughout this article, we chose the alibi approach to describe rotations.
- Pre-multiplication or post-multiplication
- The vector can be pre-multiplied by a rotation matrix (Rv, where v is a column vector), or post-multiplied by it (vR, where v is a row vector). Throughout this article, we described rotations produced by means of a pre-multiplication.
- Right- or left-handed coordinates
- The matrix and the vector can be represented with respect to a right-handed or left-handed coordinate system. Throughout the article, we assumed a right-handed orientation, unless otherwise specified.
- Vectors or forms
- The vector space has a dual space of linear forms, and the matrix can act on either vectors or forms.
In most cases the effect of the ambiguity is equivalent to the effect of a transposition of the rotation matrix.
Decompositions
Independent planes
Consider the 3×3 rotation matrix
If Q acts in a certain direction, v, purely as a scaling by a factor λ, then we have
so that
Thus λ is a root of the characteristic polynomial for Q,
Two features are noteworthy. First, one of the roots (or eigenvalues) is 1, which tells us that some direction is unaffected by the matrix. For rotations in three dimensions, this is the axis of the rotation (a concept that has no meaning in any other dimension). Second, the other two roots are a pair of complex conjugates, whose product is 1 (the constant term of the quadratic), and whose sum is 2 cos θ (the negated linear term). This factorization is of interest for 3×3 rotation matrices because the same thing occurs for all of them. (As special cases, for a null rotation the "complex conjugates" are both 1, and for a 180° rotation they are both −1.) Furthermore, a similar factorization holds for any n×n rotation matrix. If the dimension, n, is odd, there will be a "dangling" eigenvalue of 1; and for any dimension the rest of the polynomial factors into quadratic terms like the one here (with the two special cases noted). We are guaranteed that the characteristic polynomial will have degree n and thus n eigenvalues. And since a rotation matrix commutes with its transpose, it is a normal matrix, so can be diagonalized. We conclude that every rotation matrix, when expressed in a suitable coordinate system, partitions into independent rotations of two-dimensional subspaces, at most n⁄2 of them.
The sum of the entries on the main diagonal of a matrix is called the trace; it does not change if we reorient the coordinate system, and always equals the sum of the eigenvalues. This has the convenient implication for 2×2 and 3×3 rotation matrices that the trace reveals the angle of rotation, θ, in the two-dimensional (sub-)space. For a 2×2 matrix the trace is 2 cos(θ), and for a 3×3 matrix it is 1+2 cos(θ). In the three-dimensional case, the subspace consists of all vectors perpendicular to the rotation axis (the invariant direction, with eigenvalue 1). Thus we can extract from any 3×3 rotation matrix a rotation axis and an angle, and these completely determine the rotation.
Sequential angles
The constraints on a 2×2 rotation matrix imply that it must have the form
with a2+b2 = 1. Therefore we may set a = cos θ and b = sin θ, for some angle θ. To solve for θ it is not enough to look at a alone or b alone; we must consider both together to place the angle in the correct quadrant, using a two-argument arctangent function.
Now consider the first column of a 3×3 rotation matrix,
Although a2+b2 will probably not equal 1, but some value r2 < 1, we can use a slight variation of the previous computation to find a so-called Givens rotation that transforms the column to
zeroing b. This acts on the subspace spanned by the x and y axes. We can then repeat the process for the xz subspace to zero c. Acting on the full matrix, these two rotations produce the schematic form
Shifting attention to the second column, a Givens rotation of the yz subspace can now zero the z value. This brings the full matrix to the form
which is an identity matrix. Thus we have decomposed Q as
An n×n rotation matrix will have (n−1)+(n−2)+⋯+2+1, or
entries below the diagonal to zero. We can zero them by extending the same idea of stepping through the columns with a series of rotations in a fixed sequence of planes. We conclude that the set of n×n rotation matrices, each of which has n2 entries, can be parameterized by n(n−1)/2 angles.
xzxw xzyw xyxw xyzw yxyw yxzw yzyw yzxw zyzw zyxw zxzw zxyw xzxb yzxb xyxb zyxb yxyb zxyb yzyb xzyb zyzb xyzb zxzb yxzb In three dimensions this restates in matrix form an observation made by Euler, so mathematicians call the ordered sequence of three angles Euler angles. However, the situation is somewhat more complicated than we have so far indicated. Despite the small dimension, we actually have considerable freedom in the sequence of axis pairs we use; and we also have some freedom in the choice of angles. Thus we find many different conventions employed when three-dimensional rotations are parameterized for physics, or medicine, or chemistry, or other disciplines. When we include the option of world axes or body axes, 24 different sequences are possible. And while some disciplines call any sequence Euler angles, others give different names (Euler, Cardano, Tait-Bryan, Roll-pitch-yaw) to different sequences.
One reason for the large number of options is that, as noted previously, rotations in three dimensions (and higher) do not commute. If we reverse a given sequence of rotations, we get a different outcome. This also implies that we cannot compose two rotations by adding their corresponding angles. Thus Euler angles are not vectors, despite a similarity in appearance as a triple of numbers.
Nested dimensions
A 3×3 rotation matrix like
suggests a 2×2 rotation matrix,
is embedded in the upper left corner:
This is no illusion; not just one, but many, copies of n-dimensional rotations are found within (n+1)-dimensional rotations, as subgroups. Each embedding leaves one direction fixed, which in the case of 3×3 matrices is the rotation axis. For example, we have
fixing the x axis, the y axis, and the z axis, respectively. The rotation axis need not be a coordinate axis; if u = (x,y,z) is a unit vector in the desired direction, then
where cθ = cos θ, sθ = sin θ, is a rotation by angle θ leaving axis u fixed.
A direction in (n+1)-dimensional space will be a unit magnitude vector, which we may consider a point on a generalized sphere, Sn. Thus it is natural to describe the rotation group SO(n+1) as combining SO(n) and Sn. A suitable formalism is the fiber bundle,
where for every direction in the "base space", Sn, the "fiber" over it in the "total space", SO(n+1), is a copy of the "fiber space", SO(n), namely the rotations that keep that direction fixed.
Thus we can build an n×n rotation matrix by starting with a 2×2 matrix, aiming its fixed axis on S2 (the ordinary sphere in three-dimensional space), aiming the resulting rotation on S3, and so on up through Sn−1. A point on Sn can be selected using n numbers, so we again have n(n−1)/2 numbers to describe any n×n rotation matrix.
In fact, we can view the sequential angle decomposition, discussed previously, as reversing this process. The composition of n−1 Givens rotations brings the first column (and row) to (1,0,…,0), so that the remainder of the matrix is a rotation matrix of dimension one less, embedded so as to leave (1,0,…,0) fixed.
Skew parameters via Cayley's formula
Main article: Skew-symmetric matrixWhen an n×n rotation matrix, Q, does not include −1 as an eigenvalue, so that none of the planar rotations of which it is composed are 180° rotations, then Q+I is an invertible matrix. Most rotation matrices fit this description, and for them we can show that (Q−I)(Q+I)−1 is a skew-symmetric matrix, A. Thus AT = −A; and since the diagonal is necessarily zero, and since the upper triangle determines the lower one, A contains n(n−1)/2 independent numbers. Conveniently, I−A is invertible whenever A is skew-symmetric; thus we can recover the original matrix using the Cayley transform,
which maps any skew-symmetric matrix A to a rotation matrix. In fact, aside from the noted exceptions, we can produce any rotation matrix in this way. Although in practical applications we can hardly afford to ignore 180° rotations, the Cayley transform is still a potentially useful tool, giving a parameterization of most rotation matrices without trigonometric functions.
In three dimensions, for example, we have (Cayley 1846)
If we condense the skew entries into a vector, (x,y,z), then we produce a 90° rotation around the x axis for (1,0,0), around the y axis for (0,1,0), and around the z axis for (0,0,1). The 180° rotations are just out of reach; for, in the limit as x goes to infinity, (x,0,0) does approach a 180° rotation around the x axis, and similarly for other directions.
Lie theory
Lie group
We have established that n×n rotation matrices form a group, the special orthogonal group, SO(n). This algebraic structure is coupled with a topological structure, in that the operations of multiplication and taking the inverse (which here is merely transposition) are continuous functions of the matrix entries. Thus SO(n) is a classic example of a topological group. (In purely topological terms, it is a compact manifold.) Furthermore, the operations are not only continuous, but smooth, so SO(n) is a differentiable manifold and a Lie group (Baker (2003); Fulton & Harris (1991)).
Most properties of rotation matrices depend very little on the dimension, n; yet in Lie group theory we see systematic differences between even dimensions and odd dimensions. As well, there are some irregularities below n = 5; for example, SO(4) is, anomalously, not a simple Lie group, but instead isomorphic to the product of S3 and SO(3).
Lie algebra
Associated with every Lie group is a Lie algebra, a linear space equipped with a bilinear alternating product is called a bracket. The algebra for SO(n) is denoted by
and consists of all skew-symmetric n×n matrices (as implied by differentiating the orthogonality condition, I = QTQ). The bracket, [A1,A2], of two skew-symmetric matrices is defined to be A1A2−A2A1, which is again a skew-symmetric matrix. This Lie algebra bracket captures the essence of the Lie group product via infinitesimals.
For 2×2 rotation matrices, the Lie algebra is a one-dimensional vector space, multiples of
Here the bracket always vanishes, which tells us that, in two dimensions, rotations commute. Not so in any higher dimension. For 3×3 rotation matrices, we have a three-dimensional vector space with the convenient basis
The Lie brackets of these generators are as follows
We can conveniently identify any matrix in this Lie algebra with a vector in R3,
Under this identification, the so(3) bracket has a memorable description; it is the vector cross product,
The matrix identified with a vector v is also memorable, because
Notice this implies that v is in the null space of the skew-symmetric matrix with which it is identified, because v×v is always the zero vector.
Exponential map
Connecting the Lie algebra to the Lie group is the exponential map, which we define using the familiar power series for ex (Wedderburn 1934, §8.02),
For any skew-symmetric A, exp(A) is always a rotation matrix.
An important practical example is the 3×3 case, where we have seen we can identify every skew-symmetric matrix with a vector ω = uθ, where u = (x,y,z) is a unit magnitude vector. Recall that u is in the null space of the matrix associated with ω, so that if we use a basis with u as the z axis the final column and row will be zero. Thus we know in advance that the exponential matrix must leave u fixed. It is mathematically impossible to supply a straightforward formula for such a basis as a function of u (its existence would violate the hairy ball theorem), but direct exponentiation is possible, and yields
where c = cos θ⁄2, s = sin θ⁄2. We recognize this as our matrix for a rotation around axis u by angle θ. We also note that this mapping of skew-symmetric matrices is quite different from the Cayley transform discussed earlier.
In any dimension, if we choose some nonzero A and consider all its scalar multiples, exponentiation yields rotation matrices along a geodesic of the group manifold, forming a one-parameter subgroup of the Lie group. More broadly, the exponential map provides a homeomorphism between a neighborhood of the origin in the Lie algebra and a neighborhood of the identity in the Lie group. In fact, we can produce any rotation matrix as the exponential of some skew-symmetric matrix, so for these groups the exponential map is a surjection.
Baker–Campbell–Hausdorff formula
Suppose we are given A and B in the Lie algebra. Their exponentials, exp(A) and exp(B), are rotation matrices, which we can multiply. Since the exponential map is a surjection, we know that for some C in the Lie algebra, exp(A)exp(B) = exp(C), and we write
When exp(A) and exp(B) commute (which always happens for 2×2 matrices, but not higher), then C = A+B, mimicking the behavior of complex exponentiation. The general case is given by the BCH formula, a series expanded in terms of the bracket (Hall 2004, Ch. 3; Varadarajan 1984, §2.15). For matrices, the bracket is the same operation as the commutator, which detects lack of commutativity in multiplication. The general formula begins as follows.
Representation of a rotation matrix as a sequential angle decomposition, as in Euler angles, may tempt us to treat rotations as a vector space, but the higher order terms in the BCH formula reveal that to be a mistake.
We again take special interest in the 3×3 case, where [A,B] equals the cross product, A×B. If A and B are linearly independent, then A, B, and A×B can be used as a basis; if not, then A and B commute. And conveniently, in this dimension the summation in the BCH formula has a closed form (Engø 2001) as αA+βB+γ(A×B).
Spin group
The Lie group of n×n rotation matrices, SO(n), is a compact and path-connected manifold, and thus locally compact and connected. However, it is not simply connected, so Lie theory tells us it is a kind of "shadow" (a homomorphic image) of a universal covering group. Often the covering group, which in this case is the spin group denoted by Spin(n), is simpler and more natural to work with (Baker 2003, Ch. 5; Fulton & Harris 1991, pp. 299–315).
In the case of planar rotations, SO(2) is topologically a circle, S1. Its universal covering group, Spin(2), is isomorphic to the real line, R, under addition. In other words, whenever we use angles of arbitrary magnitude, which we often do, we are essentially taking advantage of the convenience of the "mother space". Every 2×2 rotation matrix is produced by a countable infinity of angles, separated by integer multiples of 2π. Correspondingly, the fundamental group of SO(2) is isomorphic to the integers, Z.
In the case of spatial rotations, SO(3) is topologically equivalent to three-dimensional real projective space, RP3. Its universal covering group, Spin(3), is isomorphic to the 3-sphere, S3. Every 3×3 rotation matrix is produced by two opposite points on the sphere. Correspondingly, the fundamental group of SO(3) is isomorphic to the two-element group, Z2. We can also describe Spin(3) as isomorphic to quaternions of unit norm under multiplication, or to certain 4×4 real matrices, or to 2×2 complex special unitary matrices.
Concretely, a unit quaternion, q, with
produces the rotation matrix
This is our third version of this matrix, here as a rotation around non-unit axis vector (x,y,z) by angle 2θ, where cos θ = w and |sin θ| = ||(x,y,z)||. (The proper sign for sin θ is implied once the signs of the axis components are decided.)
Many features of this case are the same for higher dimensions. The coverings are all two-to-one, with SO(n), n > 2, having fundamental group Z2. The natural setting for these groups is within a Clifford algebra. And the action of the rotations is produced by a kind of "sandwich", denoted by qvq∗.
Infinitesimal rotations
The matrices in the Lie algebra are not themselves rotations; the skew-symmetric matrices are derivatives, proportional differences of rotations. An actual "differential rotation", or infinitesimal rotation matrix has the form
where dθ is vanishingly small. These matrices do not satisfy all the same properties as ordinary finite rotation matrices under the usual treatment of infinitesimals (Goldstein, Poole & Safko 2002, §4.8). To understand what this means, consider
We first test the orthogonality condition, QTQ = I. The product is
differing from an identity matrix by second order infinitesimals, which we discard. So to first order, an infinitesimal rotation matrix is an orthogonal matrix. Next we examine the square of the matrix.
Again discarding second order effects, we see that the angle simply doubles. This hints at the most essential difference in behavior, which we can exhibit with the assistance of a second infinitesimal rotation,
Compare the products dAxdAy and dAydAx.
Since dθ dφ is second order, we discard it; thus, to first order, multiplication of infinitesimal rotation matrices is commutative. In fact,
again to first order. Put in other words, the order in which infinitesimal rotations are applied is irrelevant, this useful fact makes, for example, derivation of rigid body rotation relatively simple.
But we must always be careful to distinguish (the first order treatment of) these infinitesimal rotation matrices from both finite rotation matrices and from derivatives of rotation matrices (namely skew-symmetric matrices). Contrast the behavior of finite rotation matrices in the BCH formula with that of infinitesimal rotation matrices, where all the commutator terms will be second order infinitesimals so we do have a vector space.
Conversions
We have seen the existence of several decompositions that apply in any dimension, namely independent planes, sequential angles, and nested dimensions. In all these cases we can either decompose a matrix or construct one. We have also given special attention to 3×3 rotation matrices, and these warrant further attention, in both directions (Stuelpnagel 1964).
Quaternion
Main article: Quaternions and spatial rotationGiven the unit quaternion q = (w,x,y,z), the equivalent 3×3 rotation matrix is
Now every quaternion component appears multiplied by two in a term of degree two, and if all such terms are zero what's left is an identity matrix. This leads to an efficient, robust conversion from any quaternion — whether unit, nonunit, or even zero — to a 3×3 rotation matrix.
Nq = w^2 + x^2 + y^2 + z^2 if Nq > 0.0 then s = 2/Nq else s = 0.0 X = x*s; Y = y*s; Z = z*s wX = w*X; wY = w*Y; wZ = w*Z xX = x*X; xY = x*Y; xZ = x*Z yY = y*Y; yZ = y*Z; zZ = z*Z [ 1.0-(yY+zZ) xY-wZ xZ+wY ] [ xY+wZ 1.0-(xX+zZ) yZ-wX ] [ xZ-wY yZ+wX 1.0-(xX+yY) ]
Freed from the demand for a unit quaternion, we find that nonzero quaternions act as homogeneous coordinates for 3×3 rotation matrices. The Cayley transform, discussed earlier, is obtained by scaling the quaternion so that its w component is 1. For a 180° rotation around any axis, w will be zero, which explains the Cayley limitation.
The sum of the entries along the main diagonal (the trace), plus one, equals 4−4(x2+y2+z2), which is 4w2. Thus we can write the trace itself as 2w2+2w2−1; and from the previous version of the matrix we see that the diagonal entries themselves have the same form: 2x2+2w2−1, 2y2+2w2−1, and 2z2+2w2−1. So we can easily compare the magnitudes of all four quaternion components using the matrix diagonal. We can, in fact, obtain all four magnitudes using sums and square roots, and choose consistent signs using the skew-symmetric part of the off-diagonal entries.
t = Qxx+Qyy+Qzz (trace of Q) r = sqrt(1+t) w = 0.5*r x = copysign(0.5*sqrt(1+Qxx-Qyy-Qzz), Qzy-Qyz) y = copysign(0.5*sqrt(1-Qxx+Qyy-Qzz), Qxz-Qzx) z = copysign(0.5*sqrt(1-Qxx-Qyy+Qzz), Qyx-Qxy)
where copysign(x,y) is x with the sign of y:
Alternatively, use a single square root and division
t = Qxx+Qyy+Qzz r = sqrt(1+t) s = 0.5/r w = 0.5*r x = (Qzy-Qyz)*s y = (Qxz-Qzx)*s z = (Qyx-Qxy)*s
This is numerically stable so long as the trace, t, is not negative; otherwise, we risk dividing by (nearly) zero. In that case, suppose Qxx is the largest diagonal entry, so x will have the largest magnitude (the other cases are similar); then the following is safe.
t = Qxx+Qyy+Qzz r = sqrt(1+t) s = 0.5/r w = (Qzy-Qyz)*s x = 0.5*r y = (Qxy+Qyx)*s z = (Qzx+Qxz)*s
If the matrix contains significant error, such as accumulated numerical error, we may construct a symmetric 4×4 matrix,
and find the eigenvector, (w,x,y,z), of its largest magnitude eigenvalue. (If Q is truly a rotation matrix, that value will be 1.) The quaternion so obtained will correspond to the rotation matrix closest to the given matrix[dubious ] (Bar-Itzhack 2000).
Polar decomposition
If the n×n matrix M is non-singular, its columns are linearly independent vectors; thus the Gram–Schmidt process can adjust them to be an orthonormal basis. Stated in terms of numerical linear algebra, we convert M to an orthogonal matrix, Q, using QR decomposition. However, we often prefer a Q "closest" to M, which this method does not accomplish. For that, the tool we want is the polar decomposition (Fan & Hoffman 1955; Higham 1989).
To measure closeness, we may use any matrix norm invariant under orthogonal transformations. A convenient choice is the Frobenius norm, ||Q−M||F, squared, which is the sum of the squares of the element differences. Writing this in terms of the trace, Tr, our goal is,
- Find Q minimizing Tr( (Q−M)T(Q−M) ), subject to QTQ = I.
Though written in matrix terms, the objective function is just a quadratic polynomial. We can minimize it in the usual way, by finding where its derivative is zero. For a 3×3 matrix, the orthogonality constraint implies six scalar equalities that the entries of Q must satisfy. To incorporate the constraint(s), we may employ a standard technique, Lagrange multipliers, assembled as a symmetric matrix, Y. Thus our method is:
- Differentiate Tr( (Q−M)T(Q−M) + (QTQ−I)Y ) with respect to (the entries of) Q, and equate to zero.
Consider a 2×2 example. Including constraints, we seek to minimize
Taking the derivative with respect to Qxx, Qxy, Qyx, Qyy in turn, we assemble a matrix.
In general, we obtain the equation
so that
where Q is orthogonal and S is symmetric. To ensure a minimum, the Y matrix (and hence S) must be positive definite. Linear algebra calls QS the polar decomposition of M, with S the positive square root of S2 = MTM.
When M is non-singular, the Q and S factors of the polar decomposition are uniquely determined. However, the determinant of S is positive because S is positive definite, so Q inherits the sign of the determinant of M. That is, Q is only guaranteed to be orthogonal, not a rotation matrix. This is unavoidable; an M with negative determinant has no uniquely-defined closest rotation matrix.
Axis and angle
Main article: Axis-angle representationTo efficiently construct a rotation matrix Q from an angle θ and a unit axis u, we can take advantage of symmetry and skew-symmetry within the entries. If x, y, and z are the components of the unit vector representing the axis, and
c = cos(θ); s = sin(θ); C = 1-c
then Q is
[ xxC+c xyC-zs xzC+ys ] [ yxC+zs yyC+c yzC-xs ] [ zxC-ys zyC+xs zzC+c ]
Determining an axis and angle, like determining a quaternion, is only possible up to sign; that is, (u,θ) and (−u,−θ) correspond to the same rotation matrix, just like q and −q. As well, axis-angle extraction presents additional difficulties. The angle can be restricted to be from 0° to 180°, but angles are formally ambiguous by multiples of 360°. When the angle is zero, the axis is undefined. When the angle is 180°, the matrix becomes symmetric, which has implications in extracting the axis. Near multiples of 180°, care is needed to avoid numerical problems: in extracting the angle, a two-argument arctangent with atan2(sin θ,cos θ) equal to θ avoids the insensitivity of arccosine; and in computing the axis magnitude to force unit magnitude, a brute-force approach can lose accuracy through underflow (Moler & Morrison 1983).
A partial approach is as follows.
x = Qzy-Qyz y = Qxz-Qzx z = Qyx-Qxy r = sqrt(x2 + y2 + z2) t = Qxx+Qyy+Qzz (trace of matrix Q) θ = atan2(r,t−1)
The x, y, and z components of the axis would then be divided by r. A fully robust approach will use different code when the trace t is negative, as with quaternion extraction. When r is zero because the angle is zero, an axis must be provided from some source other than the matrix.
Euler angles
Complexity of conversion escalates with Euler angles (used here in the broad sense). The first difficulty is to establish which of the twenty-four variations of Cartesian axis order we will use. Suppose the three angles are θ1, θ2, θ3; physics and chemistry may interpret these as
while aircraft dynamics may use
One systematic approach begins with choosing the right-most axis. Among all permutations of (x,y,z), only two place that axis first; one is an even permutation and the other odd. Choosing parity thus establishes the middle axis. That leaves two choices for the left-most axis, either duplicating the first or not. These three choices gives us 3×2×2 = 12 variations; we double that to 24 by choosing static or rotating axes.
This is enough to construct a matrix from angles, but triples differing in many ways can give the same rotation matrix. For example, suppose we use the zyz convention above; then we have the following equivalent pairs:
-
(90°, 45°, −105°) ≡ (−270°, −315°, 255°) multiples of 360° (72°, 0°, 0°) ≡ (40°, 0°, 32°) singular alignment (45°, 60°, −30°) ≡ (−135°, −60°, 150°) bistable flip
Angles for any order can be found using a concise common routine (Herter & Lott 1993; Shoemake 1994).
The problem of singular alignment, the mathematical analog of physical gimbal lock, occurs when the middle rotation aligns the axes of the first and last rotations. It afflicts every axis order at either even or odd multiples of 90°. These singularities are not characteristic of the rotation matrix as such, and only occur with the usage of Euler angles.
The singularities are avoided when considering and manipulating the rotation matrix as orthonormal row vectors (in 3D applications often named 'right'-vector, 'up'-vector and 'out'-vector) instead of as angles. The singularities are also avoided when working with quaternions.
Uniform random rotation matrices
We sometimes need to generate a uniformly distributed random rotation matrix. It seems intuitively clear in two dimensions that this means the rotation angle is uniformly distributed between 0 and 2π. That intuition is correct, but does not carry over to higher dimensions. For example, if we decompose 3×3 rotation matrices in axis-angle form, the angle should not be uniformly distributed; the probability that (the magnitude of) the angle is at most θ should be 1⁄π(θ − sin θ), for 0 ≤ θ ≤ π.
Since SO(n) is a connected and locally compact Lie group, we have a simple standard criterion for uniformity, namely that the distribution be unchanged when composed with any arbitrary rotation (a Lie group "translation"). This definition corresponds to what is called Haar measure. León, Massé & Rivest (2006) show how to use the Cayley transform to generate and test matrices according to this criterion.
We can also generate a uniform distribution in any dimension using the subgroup algorithm of Diaconis & Shashahani (1987). This recursively exploits the nested dimensions group structure of SO(n), as follows. Generate a uniform angle and construct a 2×2 rotation matrix. To step from n to n+1, generate a vector v uniformly distributed on the n-sphere, Sn, embed the n×n matrix in the next larger size with last column (0,…,0,1), and rotate the larger matrix so the last column becomes v.
As usual, we have special alternatives for the 3×3 case. Each of these methods begins with three independent random scalars uniformly distributed on the unit interval. Arvo (1992) takes advantage of the odd dimension to change a Householder reflection to a rotation by negation, and uses that to aim the axis of a uniform planar rotation.
Another method uses unit quaternions. Multiplication of rotation matrices is homomorphic to multiplication of quaternions, and multiplication by a unit quaternion rotates the unit sphere. Since the homomorphism is a local isometry, we immediately conclude that to produce a uniform distribution on SO(3) we may use a uniform distribution on S3.
Euler angles can also be used, though not with each angle uniformly distributed (Murnaghan 1962; Miles 1965).
For the axis-angle form, the axis is uniformly distributed over the unit sphere of directions, S2, while the angle has the non-uniform distribution over [0,π] noted previously (Miles 1965).
See also
- Rotation operator (vector space)
- Rotation representation
- Kabsch algorithm
- Isometry
- Orthogonal matrix
- Rodrigues' rotation formula
- Yaw-pitch-roll system
- Plane of rotation
- Transformation matrix
Notes
- ^ W3C recommendation (2003), Scalable Vector Graphics -- the initial coordinate system, http://www.w3.org/TR/SVG/coords.html#InitialCoordinateSystem
References
- Arvo, James (1992), "Fast random rotation matrices", in David Kirk, Graphics Gems III, San Diego: Academic Press Professional, pp. 117–120, ISBN 978-0-12-409671-4, http://www.graphicsgems.org/
- Baker, Andrew (2003), Matrix Groups: An Introduction to Lie Group Theory, Springer, ISBN 978-1-85233-470-3
- Bar-Itzhack, Itzhack Y. (Nov.–Dec. 2000), "New method for extracting the quaternion from a rotation matrix", AIAA Journal of Guidance, Control and Dynamics 23 (6): 1085–1087, doi:10.2514/2.4654, ISSN 0731-5090
- Björck, A.; Bowie, C. (June 1971), "An iterative algorithm for computing the best estimate of an orthogonal matrix", SIAM Journal on Numerical Analysis 8 (2): 358–364, doi:10.1137/0708036, ISSN 0036-1429
- Cayley, Arthur (1846), "Sur quelques propriétés des déterminants gauches", Journal für die Reine und Angewandte Mathematik (Crelle's Journal), 32: 119–123, ISSN 0075-4102; reprinted as article 52 in Cayley, Arthur (1889), The collected mathematical papers of Arthur Cayley, I (1841–1853), Cambridge University Press, pp. 332–336, http://www.hti.umich.edu/cgi/t/text/pageviewer-idx?c=umhistmath;cc=umhistmath;rgn=full%20text;idno=ABS3153.0001.001;didno=ABS3153.0001.001;view=image;seq=00000349
- Diaconis, Persi; Shahshahani, Mehrdad (1987), "The subgroup algorithm for generating uniform random variables", Probability in the Engineering and Informational Sciences 1: 15–32, doi:10.1017/S0269964800000255, ISSN 0269-9648
- Engø, Kenth (June 2001), "On the BCH-formula in so(3)", BIT Numerical Mathematics 41 (3): 629–632, doi:10.1023/A:1021979515229, ISSN 0006-3835, http://www.ii.uib.no/publikasjoner/texrap/abstract/2000-201.html
- Fan, Ky; Hoffman, Alan J. (February 1955), "Some metric inequalities in the space of matrices", Proc. AMS (Proceedings of the American Mathematical Society, Vol. 6, No. 1) 6 (1): 111–116, doi:10.2307/2032662, ISSN 0002-9939, JSTOR 2032662
- Fulton, William; Harris, Joe (1991), Representation Theory: A First Course, GTM, 129, New York, Berlin, Heidelberg: Springer, ISBN 978-0-387-97495-8, MR1153249
- Goldstein, Herbert; Poole, Charles P.; Safko, John L. (2002), Classical Mechanics (third ed.), Addison Wesley, ISBN 978-0-201-65702-9
- Hall, Brian C. (2004), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Springer, ISBN 978-0-387-40122-5 (GTM 222)
- Herter, Thomas; Lott, Klaus (September–October 1993), "Algorithms for decomposing 3-D orthogonal matrices into primitive rotations", Computers & Graphics 17 (5): 517–527, doi:10.1016/0097-8493(93)90003-R, ISSN 0097-8493
- Higham, Nicholas J. (October 1 1989), "Matrix nearness problems and applications", in Gover, M. J. C.; Barnett, S., Applications of Matrix Theory, Oxford University Press, pp. 1–27, ISBN 978-0-19-853625-3, http://scholar.google.co.uk/scholar?hl=en&lr=&q=author%3AHigham+intitle%3AApplications+of+Matrix+Theory&as_publication=&as_ylo=1989&as_yhi=1989&btnG=Search
- León, Carlos A.; Massé, Jean-Claude; Rivest, Louis-Paul (February 2006), "A statistical model for random rotations", Journal of Multivariate Analysis 97 (2): 412–430, doi:10.1016/j.jmva.2005.03.009, ISSN 0047-259X, http://www.mat.ulaval.ca/pages/lpr/
- Miles, R. E. (December 1965), "On random rotations in R3", Biometrika (Biometrika, Vol. 52, No. 3/4) 52 (3/4): 636–639, doi:10.2307/2333716, ISSN 0006-3444, JSTOR 2333716
- Moler, Cleve; Morrison, Donald (1983), "Replacing square roots by pythagorean sums", IBM Journal of Research and Development 27 (6): 577–581, doi:10.1147/rd.276.0577, ISSN 0018-8646, http://domino.watson.ibm.com/tchjr/journalindex.nsf/0b9bc46ed06cbac1852565e6006fe1a0/0043d03ee1c1013c85256bfa0067f5a6?OpenDocument
- Murnaghan, Francis D. (1950), "The element of volume of the rotation group", Proceedings of the National Academy of Sciences 36 (11): 670–672, doi:10.1073/pnas.36.11.670, ISSN 0027-8424, http://www.pnas.org/content/vol36/issue11/
- Murnaghan, Francis D. (1962), The Unitary and Rotation Groups, Lectures on applied mathematics, Washington: Spartan Books
- Prentice, Michael J. (1986), "Orientation statistics without parametric assumptions", Journal of the Royal Statistical Society. Series B (Methodological) 48 (2): 214–222, ISSN 0035-9246
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 21.5.2. Picking a Random Rotation Matrix", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8, http://apps.nrbook.com/empanel/index.html#pg=1130
- Shepperd, Stanley W. (May–June 1978), "Quaternion from rotation matrix", AIAA Journal of Guidance, Control and Dynamics 1 (3): 223–224, ISSN 0731-5090
- Shoemake, Ken (1994), "Euler angle conversion", in Paul Heckbert, Graphics Gems IV, San Diego: Academic Press Professional, pp. 222–229, ISBN 978-0-12-336155-4, http://www.graphicsgems.org/
- Stuelpnagel, John (October 1964), "On the parameterization of the three-dimensional rotation group", SIAM Review 6 (4): 422–430, doi:10.1137/1006093, ISSN 0036-1445 (Also NASA-CR-53568.)
- Varadarajan, V. S. (1984), Lie Groups, Lie Algebras, and Their Representation, Springer, ISBN 978-0-387-90969-1 (GTM 102)
- Wedderburn, J. H. M. (1934), Lectures on Matrices, AMS, ISBN 978-0-8218-3204-2, http://scholar.google.co.uk/scholar?hl=en&lr=&q=author%3AWedderburn+intitle%3ALectures+on+Matrices&as_publication=&as_ylo=1934&as_yhi=1934&btnG=Search
External links
Categories:- Rotational symmetry
- Matrices
Wikimedia Foundation. 2010.


![\begin{alignat}{1}
R_x(\theta) &= \begin{bmatrix}
1 & 0 & 0 \\
0 & \cos \theta & -\sin \theta \\[3pt]
0 & \sin \theta & \cos \theta \\[3pt]
\end{bmatrix} \\[6pt]
R_y(\theta) &= \begin{bmatrix}
\cos \theta & 0 & \sin \theta \\[3pt]
0 & 1 & 0 \\[3pt]
-\sin \theta & 0 & \cos \theta \\
\end{bmatrix} \\[6pt]
R_z(\theta) &= \begin{bmatrix}
\cos \theta & -\sin \theta & 0 \\[3pt]
\sin \theta & \cos \theta & 0\\[3pt]
0 & 0 & 1\\
\end{bmatrix}.
\end{alignat}](4/5148f88bf9e6811e35615c08d2839793.png)







![R = I\cos\theta + \sin\theta[\mathbf u]_{\times} + (1-\cos\theta)\mathbf{u}\otimes\mathbf{u},](7/bd7a565caee6c8ec8eb97da5ec88a894.png)
![\mathbf{u}\otimes\mathbf{u} = \begin{bmatrix}
u_x^2 & u_x u_y & u_x u_z \\[3pt]
u_x u_y & u_y^2 & u_y u_z \\[3pt]
u_x u_z & u_y u_z & u_z^2
\end{bmatrix},\qquad [\mathbf u]_{\times} = \begin{bmatrix}
0 & -u_z & u_y \\[3pt]
u_z & 0 & -u_x \\[3pt]
-u_y & u_x & 0
\end{bmatrix}.](6/2d6ad376f5e617df67eaf3ab90ade51a.png)
































![Q_{3 \times 3} = \left[ \begin{matrix} Q_{2 \times 2} & \bold{0} \\ \bold{0}^T & 1 \end{matrix} \right] .](3/163b60290056926698849da91176ab7b.png)










![[A_{\bold{x}}, A_{\bold{y}}] = A_{\bold{z}}, \quad
[A_{\bold{z}}, A_{\bold{x}}] = A_{\bold{y}}, \quad
[A_{\bold{y}}, A_{\bold{z}}] = A_{\bold{x}}.](4/9e419c063f1acbbc88db11db7804dc98.png)

![[\tilde{\bold{u}},\tilde{\bold{v}}] = (\bold{u} \times \bold{v})^{\sim} . \,\!](8/7a8562bf54160e9d6978db5b17da0d92.png)




![A \ast B = A + B + \tfrac12 [A,B] + \tfrac{1}{12} [A,[A,B]] - \tfrac{1}{12} [B,[A,B]] - \cdots \,\!](d/22d492d59d88b1219aa7a58a065ceccc.png)

















