Electric potential energy

Electromagnetism
Electricity · Magnetism
Electrostatics Electric charge · Coulomb's law · Electric field · Electric flux · Gauss's law · Electric potential energy · Electric potential · Electrostatic induction · Electric dipole moment · Polarization density
Magnetostatics Ampère's law · Electric current · Magnetic field · Magnetization · Magnetic flux · Biot–Savart law · Magnetic dipole moment · Gauss's law for magnetism
Electrodynamics Lorentz force law · emf · Electromagnetic induction · Faraday’s law · Lenz's law · Displacement current · Maxwell's equations · EM field · Electromagnetic radiation · Liénard–Wiechert potential · Maxwell tensor · Eddy current
Electrical Network Electrical conduction · Electrical resistance · Capacitance · Inductance · Impedance · Resonant cavities · Waveguides
Covariant formulation Electromagnetic tensor · EM Stress-energy tensor · Four-current · Electromagnetic four-potential
Scientists Ampère · Coulomb · Faraday · Gauss · Heaviside · Henry · Hertz · Lorentz · Maxwell · Tesla · Volta · Weber · Ørsted
v · d · e

Not to be confused with Electric potential.

Electric potential energy, or electrostatic potential energy, is a potential energy (measured in joules) that results from conservative Coulomb forces and is associated with the configuration of a particular set of point charges within a defined system. Not to be confused with the term electric potential (measured in volts), the term "electric potential energy" is used to describe the potential energy in systems with electric fields that change with time (time variant), while the term "electrostatic potential energy" is used to describe the potential energy in systems with electric fields that do not change with time (time invariant).

The reference zero is usually taken to be a state in which the individual point charges are very well separated ("are at infinite separation") and are at rest.^[1]:§25-1 The electric potential energy of a system (U_E), relative to this zero, is equal to the total work 'W that must be done by a hypothetical external agent in order to bring the charges slowly, one by one, from infinite separation, to the stated system configuration.

$U_{\mathrm{E}} = W = k_e \frac{q_1 \cdot q_2}{r} = (\frac{1}{4 \pi \varepsilon_0}) \frac{q_1 \cdot q_2}{r} = q \cdot \Delta V = q \cdot E d. \!$

In this process the external agent is deemed to provide or absorb any relevant work, and the point charge being slowly moved gains no kinetic energy.

Sometimes reference is made to the potential energy of a charge in an electrostatic field. This actually refers to the potential energy of the system containing the charge and the other charges that created the electrostatic field.^[1]:§25-1

Electrical energy is energy newly derived from electrical potential energy. When loosely used to describe energy absorbed or delivered by an electrical circuit (for example, one provided by an electric power utility) "electrical energy" refers to energy which has been converted from electrical potential energy. This energy is supplied by the combination of electric current and electrical potential that is delivered by the circuit. At the point that this electrical potential energy has been converted to another type of energy, it ceases to be electrical potential energy. Thus, all electrical energy is potential energy before it is delivered to the end-use. Once converted from potential energy, electrical energy can always be described as another type of energy (heat, light, motion, etc.).

To calculate the work required to bring a point charge into the vicinity of other (stationary) point charges, it is sufficient to know only (a) the total field generated by the other charges and (b) the charge of the point charge being moved. The field due to the charge being moved and the values of the other charges are not required. Nonetheless, in many circumstances it is mathematically easier to add up all the pairwise potential energies (as below).

It is important to understand that orale electrostatics^{[clarification needed]} is a 18th-19th-century theory of hypothetical entities called "point charges". Electrostatics is categorically not a complete theory of the charged physical particles that make up the physical world, and which are subject to the Heisenberg uncertainty principle and other laws of quantum mechanics.

Electrostatic potential energy stored in a configuration of discrete point charges

The mutual electrostatic potential energy U_E of two charges is equal to the potential energy of a charge in the electrostatic potential generated by the other. That is to say, if charge q₁ generates an electrostatic potential $\Phi_1(\mathbf r)$, which is a function of position $\mathbf r$, then $U_\mathrm{E} = q_2 \Phi_1(\mathbf r_2)$. Doing the same calculation with respect to the other charge, we obtain $U_\mathrm{E} = q_1 \Phi_2(\mathbf r_1)$. This can be generalized to give an expression for a group of N charges q₁, q₂,..., q_N at positions r₁, r₂,..., r_N , respectively:

$U_\mathrm{E} = \frac{1}{2}\sum_{i=1}^N q_i \Phi(\mathbf{r}_i)$

where, for each i value, $\Phi(\mathbf r_i)$ is the electrostatic potential due to all point charges except the one at $\mathbf r_i$

Note: The factor of one half accounts for the 'double counting' of charge pairs. For example, consider the case of just two charges.

One point charge

Electric potential V of a one point charge Q of varying charge

The electrostatic potential energy of a system containing only one point charge is zero, as there are no other sources of electrostatic potential against which an external agent must do work in moving the point charge from infinity to its final location. One should carefully consider the possibility of the point charge interacting with its own electrostatic potential. However, since such a potential at the location of the point charge itself is infinite, this "self-energy" is intentionally excluded from an evaluation of the total (finite) electrostatic potential energy of the system. Moreover, one may argue that since the electrostatic potential due to the point charge itself provides no work in moving the point charge around, this interaction is unimportant for most purposes.

Two point charges

In a Two point charges system, Electric potential energy PE of q in the potential well created by Q1 is $\mathrm{PE} = \; q \frac{1}{4\pi\varepsilon_0} \frac{Q_1}{ r}$

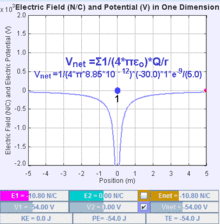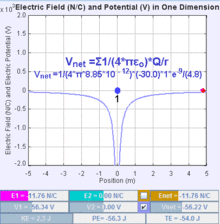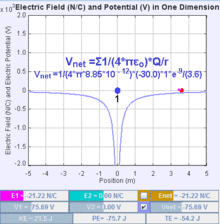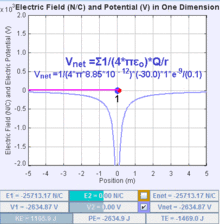
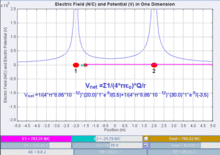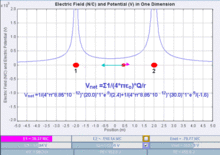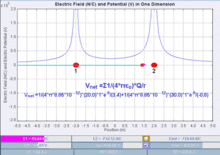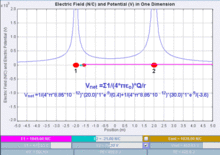
Consider bringing a second point charge, q, into its final position in the vicinity of the first point charge, Q₁. The electrostatic potential Φ(r) due to Q₁ is

$\Phi(r) = \; k_{\mathrm{e}} \frac{Q_1}{r}$

where k_e is Coulomb's constant. In the International System of Quantities, which has been the preferred international system since the 1970s and forms the basis for the definition of SI units, the Coulomb constant is given by

$k_{\mathrm{e}} = \; \frac{1}{4 \pi \varepsilon_0}$,

where ε₀ is the electric constant. Hence we obtain, potential energy if q in the potential of Q as

$\mathrm{PE} = \; q \frac{1}{4\pi\varepsilon_0} \frac{Q_1}{ r_{1}}$

where r₁ is the distance between the two point charges.

The electrostatic potential energy is negative if the charges have opposite sign and positive if the charges have the same sign. Negative mutual potential energy corresponds to attraction between two point charges; positive mutual potential energy to repulsion between two point charges.

Three or more point charges

Electrostatic potential energy of q due to Q_1 and Q_2 charge system,:$PE = q\frac{1}{4 \pi \varepsilon_0} \left(\frac{Q_1}{r_{1}} + \frac{Q_2 }{r_{2}} \right)$

The electrostatic potential energy of q due to two charges Q₁ and Q₂ should not be confused with the electrostatic potential energy of the system of three charges, because the latter also includes the electrostatic potential energy of the system of the two charges Q₁ and Q₂.

For three or more point charges, the electrostatic potential energy of the system may be calculated by the total amount of work done by an external agent in bringing individual point charges into their final positions one after another.

NOTE Here, ε₀ is the relative permittivity of free space. When the charge is in a medium other than free space / air ,the relative permittivity, ε = kε₀, has to be taken into account where k is the dielectric constant of the medium. K is the ratio of the electrostatic force on the charges in free space to the electrostatic force on the charges in the respective medium to its energy

Energy stored in an electrostatic field distribution

One may take the equation for the electrostatic potential energy of a continuous charge distribution and put it in terms of the electrostatic field.

Since Gauss' law for electrostatic field in differential form states

$\mathbf{\nabla}\cdot\mathbf{E} = \frac{\rho}{\varepsilon_0}$

where

• $\mathbf{E} \$ is the electric field vector
• $\rho \$ is the total charge density including dipole charges bound in a material,

then,

$U = \frac{1}{2}\int \limits_{\text{all space}} \rho(r) \Phi(r)d^3r$

$= \frac{1}{2}\int \limits_{\text{all space}} \varepsilon_0(\mathbf{\nabla}\cdot{\mathbf{E}})\Phi(r)d^3r$

so, now using the following divergence vector identity

$\nabla\cdot(\vec{A}{B}) = (\nabla\cdot\vec{A}){B} + \vec{A}\cdot(\nabla{B}) \Rightarrow (\nabla\cdot\vec{A}){B} = \nabla\cdot(\vec{A}{B}) - \vec{A}\cdot(\nabla{B})$

we have

$U = \frac{\varepsilon_0}{2}\int \limits_{\text{all space}} \mathbf{\nabla}\cdot(\mathbf{E}\Phi) d^3r - \frac{\varepsilon_0}{2}\int \limits_{\text{all space}} (\mathbf{\nabla}\Phi)\cdot\mathbf{E} d^3r$

using the divergence theorem and taking the area to be at infinity where $\Phi(\infty) = 0$

$U = \frac{\varepsilon_0}{2}\int \Phi\mathbf{E}\cdot dA - \frac{\varepsilon_0}{2}\int \limits_{\text{all space}} (-\mathbf{E})\cdot\mathbf{E} d^3r$

$= \int \limits_{\text{all space}} \frac{1}{2}\varepsilon_0\left|{\mathbf{E}}\right|^2 d^3r.$

So, the energy density, or energy per unit volume of the electrostatic field is:

$u_e = \frac{1}{2} \varepsilon_0 \left|{\mathbf{E}}\right|^2.$

Energy in electronic elements

Some elements in a circuit can convert energy from one form to another. For example, a resistor converts electrical energy to heat, and a capacitor stores it in its electric field.

The total electric potential energy stored in a capacitor is given by

$U_{\textrm{E}} = \frac{1}{2}QV = \frac{1}{2} CV^2 = \frac{Q^2}{2C}$

where C is the capacitance ,V is the electric potential difference, and Q the charge stored in the capacitor.

References

1. ^ ^{a b} Halliday, David; Resnick, Robert; Walker, Jearl (1997). "Electric Potential". Fundamentals of Physics (5th ed.). John Wiley & Sons. ISBN 0-471-10559-7.