- Preferred number
-
In industrial design, preferred numbers (also called preferred values) are standard guidelines for choosing exact product dimensions within a given set of constraints. Product developers must choose numerous lengths, distances, diameters, volumes, and other characteristic quantities. While all of these choices are constrained by considerations of functionality, usability, compatibility, safety or cost, there usually remains considerable leeway in the exact choice for many dimensions.
Preferred numbers serve two purposes:
- Using them increases the probability of compatibility between objects designed at different times by different people. In other words, it is one tactic among many in standardization, whether within a company or within an industry, and it is usually desirable in industrial contexts. (The opposite motive can also apply, if it is in a manufacturer's financial interest: for example, manufacturers of consumer products often have a financial interest in lack of compatibility, in planned obsolescence, and in selling name-brand and model-specific replacement parts.)
- They are chosen such that when a product is manufactured in many different sizes, these will end up roughly equally spaced on a logarithmic scale. They therefore help to minimize the number of different sizes that need to be manufactured or kept in stock.
Contents
Renard numbers
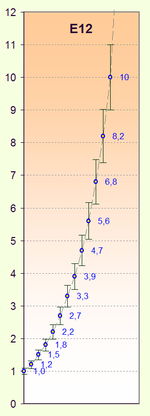
The French army engineer Col. Charles Renard proposed in the 1870s a set of preferred numbers for use with the metric system. His system was adopted in 1952 as international standard ISO 3. Renard's system of preferred numbers divides the interval from 1 to 10 into 5, 10, 20, or 40 steps. The factor between two consecutive numbers in a Renard series is constant (before rounding), namely the 5th, 10th, 20th, or 40th root of 10 (1.58, 1.26, 1.12, and 1.06, respectively), which leads to a geometric sequence. This way, the maximum relative error is minimized if an arbitrary number is replaced by the nearest Renard number multiplied by the appropriate power of 10.
These numbers may be rounded to any arbitrary precision, as they are irrational. R5, to various precisions:
Ones: 1 2 3 4 6 Tenths: 1.0 1.6 2.5 4.0 6.3 Hundredths: 1.00 1.58 2.51 3.98 6.31
Example: If our design constraints tell us that the two screws in our gadget should be placed between 32 mm and 55 mm apart, we make it 40 mm, because 4 is in the R5 series of preferred numbers.
Example: If you want to produce a set of nails with lengths between roughly 15 and 300 mm, then the application of the R5 series would lead to a product repertoire of 16 mm, 25 mm, 40 mm, 63 mm, 100 mm, 160 mm, and 250 mm long nails.
If a finer resolution is needed, another five numbers are added to the series, one after each of the original R5 numbers, and we end up with the R10 series:
R10: 1.00 1.25 1.60 2.00 2.50 3.15 4.00 5.00 6.30 8.00
Where an even finer grading is needed, the R20, R40, and R80 series can be applied:
R20: 1.00 1.25 1.60 2.00 2.50 3.15 4.00 5.00 6.30 8.00 1.12 1.40 1.80 2.24 2.80 3.55 4.50 5.60 7.10 9.00R40: 1.00 1.25 1.60 2.00 2.50 3.15 4.00 5.00 6.30 8.00 1.06 1.32 1.70 2.12 2.65 3.35 4.25 5.30 6.70 8.50 1.12 1.40 1.80 2.24 2.80 3.55 4.50 5.60 7.10 9.00 1.18 1.50 1.90 2.36 3.00 3.75 4.75 6.00 7.50 9.50R80: 1.00 1.25 1.60 2.00 2.50 3.15 4.00 5.00 6.30 8.00 1.03 1.28 1.65 2.06 2.58 3.25 4.12 5.15 6.50 8.25 1.06 1.32 1.70 2.12 2.65 3.35 4.25 5.30 6.70 8.50 1.09 1.36 1.75 2.18 2.72 3.45 4.37 5.45 6.90 8.75 1.12 1.40 1.80 2.24 2.80 3.55 4.50 5.60 7.10 9.00 1.15 1.45 1.85 2.30 2.90 3.65 4.62 5.80 7.30 9.25 1.18 1.50 1.90 2.36 3.00 3.75 4.75 6.00 7.50 9.50 1.22 1.55 1.95 2.43 3.07 3.87 4.87 6.15 7.75 9.75In some applications more rounded values are desirable, either because the numbers from the normal series would imply an unrealistically high accuracy, or because an integer value is needed (e.g., the number of teeth in a gear). For these needs, more rounded versions of the Renard series have been defined in ISO 3:
R5": 1 1.5 2.5 4 6 R10': 1 1.25 1.6 2 2.5 3.2 4 5 6.3 8 R10": 1 1.2 1.5 2 2.5 3 4 5 6 8 R20': 1 1.25 1.6 2 2.5 3.2 4 5 6.3 8 1.1 1.4 1.8 2.2 2.8 3.6 4.5 5.6 7.1 9 R20": 1 1.2 1.5 2 2.5 3 4 5 6 8 1.1 1.4 1.8 2.2 2.8 3.5 4.5 5.5 7 9 R40': 1 1.25 1.6 2 2.5 3.2 4 5 6.3 8 1.05 1.3 1.7 2.1 2.6 3.4 4.2 5.3 6.7 8.5 1.1 1.4 1.8 2.2 2.8 3.6 4.5 5.6 7.1 9 1.2 1.5 1.9 2.4 3 3.8 4.8 6 7.5 9.5As the Renard numbers repeat after every 10-fold change of the scale, they are particularly well-suited for use with SI units. It makes no difference whether the Renard numbers are used with metres or kilometres. But one would end up with two incompatible sets of nicely spaced dimensions if they were applied, for instance, with both yards and miles.
Renard numbers are rounded results of the formula
,
where b is the selected series value (for example b = 40 for the R40 series), and i is the i-th element of this series (with i = 0 through i = b).
Rail gauges
Virtually no rail gauges are preferred numbers, with two exceptions. These are likely accidental, but remarkable in that they are in the R10 series whether expressed in inches or millimeters.
The more common gauge is the Irish gauge, 63 inches, which rounds to 1600 millimeters, both numbers in the R10 series. It is also used in Australia and Brazil. The other gauge is just half this, 800 millimeters or 31.5 inches, and is used by the Wengernalpbahn in Switzerland, between Lauterbrunnen and Grindelwald by way of Kleine Scheidegg.
1-2-5 series
In applications for which the R5 series provides a too fine graduation, the 1-2-5 series is sometimes used as a cruder alternative:
- ... 0.1 0.2 0.5 1 2 5 10 20 50 100 200 500 1000 ...
This series covers a decade (1:10 ratio) in three steps. Adjacent values differ by factors 2 or 2.5. Unlike the Renard series, the 1-2-5 series has not been formally adopted as an international standard. However, the Renard series R10 can be used to extend the 1-2-5 series to a finer graduation.
This series is used to define the scales for graphs and for instruments that display in a two-dimensional form with a graticule, such as oscilloscopes.
The denominations of most modern currencies follow a 1-2-5 series. An exception are some quarter-value coins, such as the Canadian quarter and the United States quarter (the latter denominated as "quarter dollar" rather than 25 cents). A ¼-½-1 series (... 0.1 0.25 0.5 1 2.5 5 10 ...) is used by currencies derived from the former Dutch gulden (Aruban florin, Netherlands Antillean gulden, Surinamese dollar), some Middle Eastern currencies (Iraqi and Jordanian dinars, Lebanese pound, Syrian pound), and the Seychellois rupee. However, newer notes introduced in Lebanon and Syria due to inflation follow the standard 1-2-5 series instead.
E series
This graph shows how the any value between 1 and 10 is within ±10% of an E12 series value
Two decades of E12 values, which would give resistor values of 1 Ω to 82 Ω
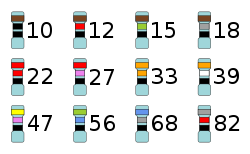A decade of the E12 values shown with their electronic color codes on resistors.In electronics, international standard IEC 60063 defines another preferred number series for resistors, capacitors, inductors and zener diodes. It works similarly to the Renard series, except that it subdivides the interval from 1 to 10 into 6, 12, 24, etc. steps. These subdivisions ensure that when some arbitrary value is replaced with the nearest preferred number, the maximum relative error will be on the order of 20%, 10%, 5%, etc.
Use of the E series is mostly restricted to resistors, capacitors and inductors. Commonly produced dimensions for other types of electrical components are either chosen from the Renard series instead (for example fuses) or are defined in relevant product standards (for example wires).
The IEC 60063 numbers are as follows. The E6 series is every other element of the E12 series, which is in turn every other element of the E24 series:
E6 ( 20%): 10 15 22 33 47 68
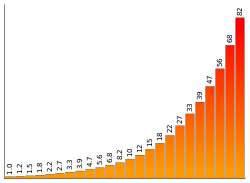
E12 ( 10%): 10 12 15 18 22 27 33 39 47 56 68 82
E24 ( 5%): 10 12 15 18 22 27 33 39 47 56 68 82 11 13 16 20 24 30 36 43 51 62 75 91With the E48 series, a third decimal place is added, and the values are slightly adjusted. Again, the E48 series is every other value of the E96 series, which is every other value of the E192 series:
E48 ( 2%): 100 121 147 178 215 261 316 383 464 562 681 825 105 127 154 187 226 274 332 402 487 590 715 866 110 133 162 196 237 287 348 422 511 619 750 909 115 140 169 205 249 301 365 442 536 649 787 953E96 ( 1%): 100 121 147 178 215 261 316 383 464 562 681 825 102 124 150 182 221 267 324 392 475 576 698 845 105 127 154 187 226 274 332 402 487 590 715 866 107 130 158 191 232 280 340 412 499 604 732 887 110 133 162 196 237 287 348 422 511 619 750 909 113 137 165 200 243 294 357 432 523 634 768 931 115 140 169 205 249 301 365 442 536 649 787 953 118 143 174 210 255 309 374 453 549 665 806 976E192 (0.5%) 100 121 147 178 215 261 316 383 464 562 681 825 101 123 149 180 218 264 320 388 470 569 690 835 102 124 150 182 221 267 324 392 475 576 698 845 104 126 152 184 223 271 328 397 481 583 706 856 105 127 154 187 226 274 332 402 487 590 715 866 106 129 156 189 229 277 336 407 493 597 723 876 107 130 158 191 232 280 340 412 499 604 732 887 109 132 160 193 234 284 344 417 505 612 741 898 110 133 162 196 237 287 348 422 511 619 750 909 111 135 164 198 240 291 352 427 517 626 759 920 113 137 165 200 243 294 357 432 523 634 768 931 114 138 167 203 246 298 361 437 530 642 777 942 115 140 169 205 249 301 365 442 536 649 787 953 117 142 172 208 252 305 370 448 542 657 796 965 118 143 174 210 255 309 374 453 549 665 806 976 120 145 176 213 258 312 379 459 556 673 816 988The E192 series is also used for 0.25% and 0.1% tolerance resistors.
1% resistors are available in both the E24 values and the E96 values.
Buildings
In the construction industry, it was felt that typical dimensions must be easy to use in mental arithmetic. Therefore, rather than using elements of a geometric series, a different system of preferred dimensions has evolved in this area, known as "modular coordination".
Major dimensions (e.g., grid lines on drawings, distances between wall centers or surfaces, widths of shelves and kitchen components) are multiples of 100 mm, i.e. one decimetre. This size is called the "basic module" (and represented in the standards by the letter M). Preference is given to the multiples of 300 mm (3 M) and 600 mm (6 M) of the basic module (see also "metric foot"). For larger dimensions, preference is given to multiples of the modules 12 M (= 1.2 m), 15 M (= 1.5 m), 30 M (= 3 m), and 60 M (= 6 m). For smaller dimensions, the submodular increments 50 mm or 25 mm are used. (ISO 2848, BS 6750)
Dimensions chosen this way can easily be divided by a large number of factors without ending up with millimetre fractions. For example, a multiple of 600 mm (6 M) can always be divided into 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 25, 30, etc. parts, each of which is again an integral number of millimetres.
Paper documents, envelopes, and drawing pens
Main article: Paper sizeStandard metric paper sizes use the square root of two and related numbers (√√√2, √√2, √2, 2, or 2√2) as factors between neighbor dimensions (Lichtenberg series, ISO 216). The √2 factor also appears between the standard pen thicknesses for technical drawings (0.13, 0.18, 0.25, 0.35, 0.50, 0.70, 1.00, 1.40, and 2.00 mm). This way, the right pen size is available to continue a drawing that has been magnified to a different standard paper size.
Computer engineering
When dimensioning computer components, the powers of two are frequently used as preferred numbers:
1 2 4 8 16 32 64 128 256 512 1024 ...
Where a finer grading is needed, additional preferred numbers are obtained by multiplying a power of two with a small odd integer:
(×3) 6 12 24 48 96 192 384 768 1536 ... (×5) 10 20 40 80 160 320 640 1280 2560 ... (×7) 14 28 56 112 224 448 896 1792 3584 ...
Preferred aspect ratios 16: 15: 12: :8 2:1 3:2 :9 16:9 5:3 4:3 :10 8:5 3:2 :12 4:3 5:4 1:1 In computer graphics, widths and heights of raster images are preferred to be multiples of 16, as many compression algorithms (JPEG, MPEG) divide color images into square blocks of that size. Black-and-white JPEG images are divided into 8x8 blocks. Screen resolutions often follow the same principle. Preferred aspect ratios have also an important influence here, e.g. 2:1, 3:2, 4:3, 5:3, 5:4, 8:5, 16:9.
Retail packaging
In some countries, consumer-protection laws restrict the number of different prepackaged sizes in which certain products can be sold, in order to make it easier for consumers to compare prices.
An example of such a regulation is the European Union directive on the volume of certain prepackaged liquids (75/106/EEC [1]). It restricts the list of allowed wine-bottle sizes to 0.1, 0.25 (1/4), 0.375 (3/8), 0.5 (1/2), 0.75 (3/4), 1, 1.5, 2, 3, and 5 litres. Similar lists exist for several other types of products. They vary and often deviate significantly from any geometric series in order to accommodate traditional sizes when feasible. Adjacent package sizes in these lists differ typically by factors 2/3 or 3/4, in some cases even 1/2, 4/5, or some other ratio of two small integers.
Music
Main article: tuning systemWhile some instruments (trombone, theremin, etc.) can play a tone at any arbitrary frequency, other instruments (such as pianos) can only play a limited set of tones. The very popular "twelve-tone equal temperament" selects tones from the geometric sequence
where k is typically 440 Hz, though other standards have been used. However, other less common tuning systems have also been historically important as preferred audio frequencies.
Since 210≈103, 21/12≈103/120=101/40, and the resultant frequency spacing is very similar to the R40 series.
Photography
In photography, aperture, exposure, and film speed generally follow powers of 2:
The aperture size controls how much light enters the camera. It's measured in f-stops: f/1.4, f/2, f/2.8, f/4, etc. Full f-stops are a square root of 2 apart. Digital cameras often subdivide these into thirds, so each f-stop is a sixth root of 2, rounded to two significant digits: 1.0, 1.1, 1.2, 1.4, 1.6, 1.8, 2.0, 2.2, 2.5, 2.8, 3.2, 3.5, 4.0.
The film speed (or digital equivalent) controls how quickly light is recorded. It's expressed as ISO values such as ISO 100, ISO 200, ISO 400, ISO 800. These are usually a power of 2 apart from each other, although other film speeds do exist.
The shutter speed controls how long the camera records light. These are expressed as fractions of a second, roughly but not exactly based on powers of 2: 1 second, 1/2, 1/4, 1/8, 1/15, 1/30, 1/60, 1/125, 1/250, 1/500, 1/1000 of a second.
References
- ISO 3, Preferred numbers — Series of preferred numbers. International Organization for Standardization, 1973.
- ISO 17, Guide to the use of preferred numbers and of series of preferred numbers. 1973.
- ISO 497, Guide to the choice of series of preferred numbers and of series containing more rounded values of preferred numbers. 1973.
- ISO 2848, Building construction — Modular coordination — Principles and rules. 1984.
- ISO/TR 8389, Building construction — Modular coordination — System of preferred numbers defining multimodular sizes. International Organization for Standardization, 1984.
- IEC 60063, Preferred number series for resistors and capacitors. International Electrotechnical Commission, 1963
- 75/106/EEC [2], European Union Directive on volume of liquids. 1975.
- BS 2045, Preferred numbers. British Standards Institution, 1965.
- BS 2488, Schedule of preferred numbers for the resistance of resistors and the capacitance of capacitors for telecommunication equipment. 1966.
- ANSI Z17.1, American National Standard for Preferred Numbers. 1973
Categories:- Numbers
- ISO standards
- Standards
- Industrial design
- Electrical components
Wikimedia Foundation. 2010.
