Birefringence

Displacement of light rays with perpendicular polarization through a birefringent material.

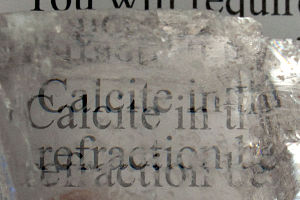A calcite crystal laid upon a paper with all letters showing the double refraction

A calcite crystal seen through a polarizing filter

Birefringence, or double refraction, is the decomposition of a ray of light into two rays when it passes through certain anisotropic materials, such as crystals of calcite or boron nitride. The effect was first described by the Danish scientist Rasmus Bartholin in 1669, who saw it in calcite.^[1] The effect is now known to also occur in certain plastics, magnetic materials, various noncrystalline materials, and liquid crystals.^[2]

The simplest instance of the effect arises in materials with uniaxial anisotropy. That is, the structure of the material is such that it has an axis of symmetry with no equivalent axis in the plane perpendicular to it. (Cubic crystals are thereby ruled out.) This axis is known as the optical axis of the material, and light with linear polarizations parallel and perpendicular to it has unequal indices of refraction, denoted n_e and n_o, respectively, where the suffixes stand for extraordinary and ordinary. The names reflect the fact that, if unpolarized light enters the material at a nonzero acute angle to the optical axis, the component with polarization perpendicular to this axis will be refracted as per the standard law of refraction, while the complementary polarization component will refract at a nonstandard angle determined by the angle of entry and the difference between the indices of refraction,

$\Delta n=n_e-n_o\,$

known as the birefringence magnitude. The light will therefore split into two linearly polarized beams, known as ordinary and extraordinary. Exceptions arise when the light propagates either along or orthogonal to the optical axis. In the first case, both polarizations and rays are ordinary and are not split. In the second case also, there is no splitting of the light into two separate directions, but the ordinary and extraordinary components travel at different speeds, and the effect is used to interconvert between linear and circular or elliptical polarizations.

Double refraction also occurs in biaxially anisotropic materials, which are also known as trirefringent, but its description is then substantially more complex.^[3]

Creation

While birefringence is often found naturally (like anisotropic crystals), there are several ways to create it in optically isotropic materials:

• Birefringence results when isotropic materials are deformed such that the isotropy is lost in one direction (i.e., stretched or bent). Example
• By the Pockels effect, where an electric field can induce molecules to line up or behave asymmetrically, inducing anisotropy;
• by the Faraday effect, where a magnetic field can cause a material to be circularly birefringent, with different indices of refraction for oppositely-handed circular polarizations similar to an optically active material;
• by self or forced alignment of highly polar molecules such as lipids, some surfactants or liquid crystals, that generate highly birefringent thin films.

Examples of uniaxial birefringent materials

Uniaxial materials, at 590 nm^[4]

Material	no	ne	Δn
beryl Be3Al2(SiO3)6	1.602	1.557	-0.045
calcite CaCO3	1.658	1.486	-0.172
calomel Hg2Cl2	1.973	2.656	+0.683
ice H2O	1.309	1.313	+0.004
lithium niobate LiNbO3	2.272	2.187	-0.085
magnesium fluoride MgF2	1.380	1.385	+0.006
quartz SiO2	1.544	1.553	+0.009
ruby Al2O3	1.770	1.762	-0.008
rutile TiO2	2.616	2.903	+0.287
peridot (Mg, Fe)2SiO4	1.690	1.654	-0.036
sapphire Al2O3	1.768	1.760	-0.008
sodium nitrate NaNO3	1.587	1.336	-0.251
tourmaline (complex silicate )	1.669	1.638	-0.031
zircon, high ZrSiO4	1.960	2.015	+0.055
zircon, low ZrSiO4	1.920	1.967	+0.047

The best-studied uniaxial birefringent materials are crystalline, the refractive indices of several of which tabulated to the right (at wavelength ~ 590 nm).^[4] Silicon carbide, also known as Moissanite, is strongly birefringent.

Many plastics are birefringent, because their molecules are 'frozen' in a stretched conformation when the plastic is moulded or extruded.^[5] For example, cellophane is a cheap birefringent material, and Polaroid sheets are commonly used to examine for orientation in birefringent plastics like polystyrene and polycarbonate. Birefringent materials are used in many devices that manipulate the polarization of light, such as wave plates, polarizing prisms, and Lyot filters.

As stated above, birefringence can also arise in magnetic materials, but substantial variations in magnetic permeability of materials are rare at optical frequencies.

Birefringence can be observed in amyloid plaque deposits such as are found in the brains of Alzheimer's patients. Modified proteins such as immunoglobulin light chains abnormally accumulate between cells, forming fibrils. Multiple folds of these fibers line up and take on a beta-pleated sheet conformation. Congo red dye intercalates between the folds and, when observed under polarized light, causes birefringence.

Cotton (Gossypium hirsutum) fiber is birefringent because of high levels of cellulosic material in the fiber's secondary cell wall.

Slight imperfections in optical fiber can cause birefringence, which can cause distortion in fiber-optic communication; see polarization mode dispersion. The imperfections can be geometrically based, or a result of photoelastic effects from loading on the optical fiber.

Fast and slow rays

Effective refractive indices in negative uniaxial materials

Propagation direction	Ordinary ray		Extraordinary ray
	Polarization	neff	Polarization	neff
z	xy-plane	no	n/a	n/a
xy-plane	xy-plane	no	z	ne
xz-plane	y	no	xz-plane	ne < n < no
other	analogous to xz-plane

For a given propagation direction, in general there are two perpendicular polarizations for which the medium behaves as if it had a single effective refractive index. In a uniaxial material, rays with these polarizations are called the extraordinary and the ordinary ray (e and o rays), corresponding to the extraordinary and ordinary refractive indices. In a biaxial material, there are three refractive indices α, β, and γ, yet only two rays, which are called the fast and the slow ray. The slow ray is the ray that has the highest effective refractive index.

For a uniaxial material with the z axis defined to be the optical axis, the effective refractive indices are as in the table on the right. For rays propagating in the xz plane, the effective refractive index of the e polarization varies continuously between n_o and n_e, depending on the angle with the z axis. The effective refractive index can be constructed from the Index ellipsoid.

Biaxial birefringence

Biaxial materials, at 590 nm^[4]

Material	nα	nβ	nγ
borax	1.447	1.469	1.472
epsom salt MgSO4·7(H2O)	1.433	1.455	1.461
mica, biotite	1.595	1.640	1.640
mica, muscovite	1.563	1.596	1.601
olivine (Mg, Fe)2SiO4	1.640	1.660	1.680
perovskite CaTiO3	2.300	2.340	2.380
topaz	1.618	1.620	1.627
ulexite	1.490	1.510	1.520

Biaxial birefringence, also known as trirefringence, describes an anisotropic material that has more than one axis of anisotropy. For such a material, the refractive index tensor n, will in general have three distinct eigenvalues that can be labeled n_α, n_β and n_γ.

Positive or negative

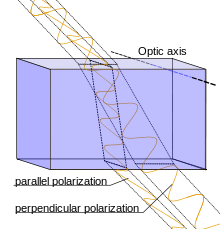Rays passing through a positively birefringent material. The incident light is having parallel and perpendicular polarisation components (unpolarised light). The optical axis is perpendicular to the direction of the perpendicular component of incident ray, so the ray polarized parallel to the optic axis has a greater refractive index than the ray polarized perpendicular to it.

Uniaxial birefringent materials are classified as positively (or negatively) birefringent when, for light (having parallel and perpendicular components) directed to the optic axis, the refractive index of light polarized parallel to the optic axis is greater (or smaller, respectively) than light polarized perpendicularly to the optic axis.^[6] In other words, the polarization of the slow (or fast) wave is parallel to the optical axis when the birefringence of the crystal is positive (or negative, respectively).

Biaxial crystals are defined as positively (or negatively) birefringent when the slow ray (or fast ray, respectively) bisects the acute angle formed by the optical axes.^[7]

In practice, when using an optical compensator that emits red light, a crystal with positive birefringence appears blue when its long dimension is parallel to the slow axis of the compensator. In contrast, a crystal with negative birefringence appears yellow when its long dimension is parallel to the slow axis of the compensator, and the slow ray of the compensator is oriented perpendicularly to the long axis of the crystal.^[7] The reason for these phenomena is that the wavelength of emitted light is shifted higher in positively birefringent crystals, because the slow ray of the crystal is parallel to the slow axis of the compensator,^[7] while for negatively birefringent crystals the wavelength of emitted light is shifted lower, because the fast ray of the crystal is parallel to the slow axis of the compensator.^[7] The order of colors resulting from the use of compensators in a polarized light system differs from that of a typical spectrum, instead having an order including yellow-orange-red-violet-blue.^[7]

Measurement

Birefringence and related optical effects (such as optical rotation and linear or circular dichroism) can be measured by measuring the changes in the polarization of light passing through the material. These measurements are known as polarimetry.

Birefringence of lipid bilayers can be measured using dual polarisation interferometry. This provides a measure of the degree of order within these fluid layers and how this order is disrupted when the layer interacts with other biomolecules.

A common feature of optical microscopes is a pair of crossed polarizing filters. Between the crossed polarizers, a birefringent sample will appear bright against a dark (isotropic) background.

For a fixed composition such as calcium carbonate, a crystal such as calcite or its polymorphs, the index of refraction depends on the direction of light through the crystal structure. The refraction also depends on composition, and can be calculated using the Gladstone-Dale relation.

Applications

A calcite crystal laid upon a paper with some letters showing the double refraction

Birefringence is widely used in optical devices, such as liquid crystal displays, light modulators, color filters, wave plates, optical axis gratings, etc. It also plays an important role in second harmonic generation and many other nonlinear processes.

Birefringent filters are also used as spatial low-pass filters in electronic cameras, where the thickness of the crystal is controlled to spread the image in one direction, thus increasing the spot-size. This is essential to the proper working of all television and electronic film cameras, to avoid spatial aliasing, the folding back of frequencies higher than can be sustained by the pixel matrix of the camera.

Medicine

Birefringence is utilized in medical diagnostics.

Urate crystals, with the crystals with their long axis seen as horizontal in this view being parallel to that of a red compensator filter. These appear as yellow, and are thereby of negative birefringence.

Needle aspiration of fluid from a gouty joint will reveal negatively birefringent monosodium urate crystals. Calcium pyrophosphate crystals, in contrast, show weak positive birefringence.^[8] In practice, urate crystals appear yellow and calcium pyrophosphate crystals appear blue when their long axes are aligned parallel to that of a red compensator filter,^[9] or a crystal of known birefringence is added to the sample for comparison.

In ophthalmology, scanning laser polarimetry utilises the birefringence of the retinal nerve fibre layer to indirectly quantify its thickness, which is of use in the assessment and monitoring of glaucoma.

Birefringence characteristics in sperm heads allow for the selection of spermatozoa for intracytoplasmic sperm injection.^[10] Likewise, zona imaging uses birefringence on oocytes to select the ones with highest chances of successful pregnancy.^[11] Birefringence of particles biopsied from pulmonary nodules indicates silicosis.

Elastic birefringence

Another form of birefringence is observed in anisotropic elastic materials. In these materials, shear waves split according to similar principles as the light waves discussed above. The study of birefringent shear waves in the earth is a part of seismology. Birefringence is also used in optical mineralogy to determine the chemical composition, and history of minerals and rocks.

Stress induced birefringence

Color pattern of a plastic box with "frozen in" mechanical stress placed between two crossed polarizers.

Isotropic solids do not exhibit birefringence. However, when they are under mechanical stress, birefringence results. The stress can be applied externally or is ‘frozen’ in after a birefringent plastic ware is cooled after it is manufactured using injection molding. When such a sample is placed between two crossed polarizers, colour patterns can be observed, because polarization of a light ray is rotated after passing through a birefingent material and the amount of rotation is dependent on wavelength. The experimental method called photoelasticity used for analyzing stress distribution in solids is based on the same principle.

Theory

More generally, birefringence can be defined by considering a dielectric permittivity and a refractive index that are tensors. Consider a plane wave propagating in an anisotropic medium, with a relative permittivity tensor ε, where the refractive index n, is defined by $n\cdot n = \epsilon$. If the wave has an electric vector of the form:

$\mathbf{E=E_0}\exp i(\mathbf{k \cdot r}-\omega t) \,$ (2)

where r is the position vector and t is time, then the wave vector k and the angular frequency ω must satisfy Maxwell's equations in the medium, leading to the equations:

$-\nabla \times \nabla \times \mathbf{E}=\frac{1}{c^2}(\mathbf{\epsilon} \cdot \frac{\part^2 \mathbf{E} }{\partial t^2})$ (3a)

$\nabla \cdot (\mathbf{\epsilon} \cdot \mathbf{E}) =0$ (3b)

where c is the speed of light in a vacuum. Substituting eqn. 2 in eqns. 3a-b leads to the conditions:

$|\mathbf{k}|^2\mathbf{E_0}-\mathbf{(k \cdot E_0) k}= \frac{\omega^2}{c^2} (\mathbf{\epsilon} \cdot \mathbf{E_0})$ (4a)

$\mathbf{k} \cdot (\mathbf{\epsilon} \cdot \mathbf{E_0}) =0$ (4b)

For the matrix product $(\epsilon\cdot\mathbf E)$ often a separate name is used, the dielectric displacement vector $\mathbf D$. So essentially birefringence concerns the general theory of linear relationships between these two vectors in anisotropic media.

To find the allowed values of k, E₀ can be eliminated from eq 4a. One way to do this is to write eqn 4a in Cartesian coordinates, where the x, y and z axes are chosen in the directions of the eigenvectors of ε, so that

$\mathbf{\epsilon}=\begin{bmatrix} n_x^2 & 0 & 0 \\ 0& n_y^2 & 0 \\ 0& 0& n_z^2 \end{bmatrix} \,$ (4c)

Hence eqn 4a becomes

$(-k_y^2-k_z^2+\frac{\omega^2n_x^2}{c^2})E_x + k_xk_yE_y + k_xk_zE_z =0$ (5a)

$k_xk_yE_x + (-k_x^2-k_z^2+\frac{\omega^2n_y^2}{c^2})E_y + k_yk_zE_z =0$ (5b)

$k_xk_zE_x + k_yk_zE_y + (-k_x^2-k_y^2+\frac{\omega^2n_z^2}{c^2})E_z =0$ (5c)

where E_x, E_y, E_z, k_x, k_y and k_z are the components of E₀ and k. This is a set of linear equations in E_x, E_y, E_z, and they have a non-trivial solution if their determinant is zero:

$\det\begin{bmatrix} (-k_y^2-k_z^2+\frac{\omega^2n_x^2}{c^2}) & k_xk_y & k_xk_z \\ k_xk_y & (-k_x^2-k_z^2+\frac{\omega^2n_y^2}{c^2}) & k_yk_z \\ k_xk_z & k_yk_z & (-k_x^2-k_y^2+\frac{\omega^2n_z^2}{c^2}) \end{bmatrix} =0\,$ (6)

Multiplying out eqn (6), and rearranging the terms, we obtain

$\frac{\omega^4}{c^4} - \frac{\omega^2}{c^2}\left(\frac{k_x^2+k_y^2}{n_z^2}+\frac{k_x^2+k_z^2}{n_y^2}+\frac{k_y^2+k_z^2}{n_x^2}\right) + \left(\frac{k_x^2}{n_y^2n_z^2}+\frac{k_y^2}{n_x^2n_z^2}+\frac{k_z^2}{n_x^2n_y^2}\right)(k_x^2+k_y^2+k_z^2)=0\,$ (7)

In the case of a uniaxial material, where n_x=n_y=n_o and n_z=n_e say, eqn 7 can be factorised into

$\left(\frac{k_x^2}{n_o^2}+\frac{k_y^2}{n_o^2}+\frac{k_z^2}{n_o^2} -\frac{\omega^2}{c^2}\right)\left(\frac{k_x^2}{n_e^2}+\frac{k_y^2}{n_e^2}+\frac{k_z^2}{n_o^2} -\frac{\omega^2}{c^2}\right)=0\,.$ (8)

Each of the factors in eqn 8 defines a surface in the space of vectors k — the surface of wave normals. The first factor defines a sphere and the second defines an ellipsoid. Therefore, for each direction of the wave normal, two wavevectors k are allowed. Values of k on the sphere correspond to the ordinary rays while values on the ellipsoid correspond to the extraordinary rays.

For a biaxial material, eqn (7) cannot be factorized in the same way, and describes a more complicated pair of wave-normal surfaces.^[12]

Birefringence is often measured for rays propagating along one of the optical axes (or measured in a two-dimensional material). In this case, n has two eigenvalues that can be labeled n₁ and n₂. n can be diagonalized by:

$\mathbf{n} = \mathbf{R(\chi)} \cdot \begin{bmatrix} n_1 & 0 \\ 0 & n_2 \end{bmatrix} \cdot \mathbf{R(\chi)}^\textrm{T}$ (9)

where R(χ) is the rotation matrix through an angle χ. Rather than specifying the complete tensor n, we may now simply specify the magnitude of the birefringence Δn, and extinction angle χ, where Δn = n₁ − n₂.

Vacuum birefringence

Due to quantum effects, the vacuum can behave like a birefringent medium. In the limit of weak fields and slowly varying fields, the Euler-Heisenberg Lagrangian becomes:

$\mathcal{L} = \frac{1}{2}\left(\mathbf{E}^{2}-\mathbf{B}^{2}\right)+\frac{2\alpha^{2}}{45 m^{4}}\left[\left(\mathbf{E}^2 - \mathbf{B}^2\right)^{2} + 7 \left(\mathbf{E}\cdot\mathbf{B}\right)^{2}\right]$

where α is the fine sructure constant and m the electron mass.

The effective electric permittivity tensor and magnetic permeability tensor are then given by ^[13]:

$\begin{align} \epsilon_{ik}&= \left[1 + \frac{8\alpha^{2}}{45 m^{4}}\left(\mathbf{E}^{2} - \mathbf{B}^{2}\right)\right]\delta_{ik} + \frac{28\alpha^{2}}{45 m^{4}}B_{i}B_{k}\\ \mu_{ik}&=\left[1 - \frac{8\alpha^{2}}{45 m^{4}}\left(\mathbf{E}^{2} - \mathbf{B}^{2}\right)\right]\delta_{ik} + \frac{28\alpha^{2}}{45 m^{4}}E_{i}E_{k} \end{align}$

In the case of an plane wave propagating through a region of constant magnetic field, one finds that there are two eigenmodes. One has the electric component of the plane wave perpendicular to the plane spanned by the wavevector and the magnetic field, the other has the magnetic component perpendicular to this plane. The former has an index of refraction of $1 + \frac{8\alpha^{2}}{45 m^{4}}B^{2}\sin^{2}(\theta)$ where θ is the angle between the wave vector and the magnetic field, while the latter has an index of refraction of $1 + \frac{14\alpha^{2}}{45 m^{4}}B^{2}\sin^{2}(\theta)$.

See also

• Cotton-Mouton effect
• Crystal optics
• John Kerr
• Periodic poling
• Dichroism

References

1. ^ Erasmus Bartholin, Experimenta crystalli islandici disdiaclastici quibus mira & infolita refractio detegitur [Experiments on birefringent Icelandic crystal through which is detected a remarkable and unique refraction] (Copenhagen, Denmark: Daniel Paulli, 1669). See also: Erasmus Bartholin (January 1, 1670) "An account of sundry experiments made and communicated by that learn'd mathematician, Dr. Erasmus Bartholin, upon a chrystal-like body, sent to him out of Island," Philosophical Transactions of the Royal Society of London, vol. 5, pages 2039-2048.
2. ^ The Science of Color, by Steven K. Shevell, Optical Society of America. Published 2003. ISBN 0444512519
3. ^ Landau, L. D., and Lifshitz, E. M., Electrodynamics of Continuous Media, Vol. 8 of the Course of Theoretical Physics 1960 (Pergamon Press), §79
4. ^ ^{a b c} Elert, Glenn. "Refraction". The Physics Hypertextbook. http://hypertextbook.com/physics/waves/refraction/. 
5. ^ The Use of Birefringence for Predicting the Stiffness of Injection Moulded Polycarbonate Discs
6. ^ Brad Amos.Birefringence for facetors I : what is birefringence? First published in StoneChat, the Journal of the UK Facet Cutter's Guild. January–March. edition 2005
7. ^ ^{a b c d e} Page 509 in:McClatchey, Kenneth D. (2002). Clinical laboratory medicine. Philadelphia: Lippincott Wiliams & Wilkins. ISBN 0-683-30751-7.  [1]
8. ^ Hardy RH, Nation B (June 1984). "Acute gout and the accident and emergency department". Arch Emerg Med 1 (2): 89–95. PMC 1285204. PMID 6536274. http://www.pubmedcentral.nih.gov/articlerender.fcgi?tool=pmcentrez&artid=1285204. 
9. ^ The Approach to the Painful Joint Workup Author: Alan N Baer; Chief Editor: Herbert S Diamond. Updated: Nov 22, 2010
10. ^ Gianaroli L, Magli MC, Ferraretti AP, et al. (December 2008). "Birefringence characteristics in sperm heads allow for the selection of reacted spermatozoa for intracytoplasmic sperm injection". Fertil. Steril. 93 (3): 807–13. doi:10.1016/j.fertnstert.2008.10.024. PMID 19064263. 
11. ^ Ebner T, Balaban B, Moser M, et al. (May 2009). "Automatic user-independent zona pellucida imaging at the oocyte stage allows for the prediction of preimplantation development". Fertil. Steril. 94 (3): 913–920. doi:10.1016/j.fertnstert.2009.03.106. PMID 19439291. 
12. ^ Born M, and Wolf E, Principles of Optics, 7th Ed. 1999 (Cambridge University Press), §15.3.3
13. ^ W. Dittrich and H. Gies, Vacuum Birefringence in Strong Magnetic Fields, preprint

External links

• http://www.olympusmicro.com/primer/lightandcolor/birefringence.html
• [2] Video of stress birefringence in Polymethylmethacrylate (PMMA or Plexiglas).
• Application note on the theory of birefringence (see no.14)
• Artist Austine Wood Comarow employs birefringence to create kinetic figurative images.