Critical point (thermodynamics)

Carbon dioxide creating a fog when cooling from supercritical to critical temperature

In physical chemistry, thermodynamics, chemistry and condensed matter physics, a critical point, also called a critical state, specifies the conditions (temperature, pressure and sometimes composition) at which a phase boundary ceases to exist. There are multiple types of critical points such as vapor–liquid critical points and liquid–liquid critical points.

Pure substances: vapor–liquid critical point

The term "critical point" is sometimes used to denote specifically the vapor–liquid critical point of a material. The vapor–liquid critical point denotes the conditions above which distinct liquid and gas phases do not exist.

The vapor–liquid critical point in a pressure–temperature phase diagram is at the high-temperature extreme of the liquid–gas phase boundary. The dotted green line gives the anomalous behaviour of water.

As shown in the pure species phase diagram to the right, this is the point at which the phase boundary between liquid and gas terminates. In water, the critical point occurs at around 647 K (374 °C; 705 °F) and 22.064 MPa (3200 PSIA or 218 atm)^[1].

As the critical temperature is approached, the properties of the gas and liquid phases approach one another, resulting in only one phase at the critical point: a homogeneous supercritical fluid. The heat of vaporization is zero at and beyond this critical point, so there is no distinction between the two phases. Above the critical temperature a liquid cannot be formed by an increase in pressure, but with enough pressure a solid may be formed. The critical pressure is the vapor pressure at the critical temperature. On the diagram showing the thermodynamic properties for a given substance, the point at which critical temperature and critical pressure meet is called the critical point of the substance. The critical molar volume is the volume of one mole of material at the critical temperature and pressure.

Critical properties vary from material to material, just as is the case for the melting point and boiling point. Critical properties for many pure substances are readily available in the literature. Obtaining critical properties for mixtures is somewhat more problematic.

Mathematical definition

For pure substances, there is an inflection point in the critical isotherm (or temperature contour line) on a pV diagram. This means that at the critical point:

$\left(\frac{\partial p}{\partial V}\right)_T = \left(\frac{\partial^2p}{\partial V^2}\right)_T = 0$

This relation can be used to evaluate two parameters for an equation of state in terms of the critical properties.

Sometimes a set of reduced properties are defined in terms of the critical properties, i.e.:^[2]

$T_r = T/T_c\,$

$p_r = p/p_c\,$

$V_r = \frac{V}{RT_c/p_c}\,$

where T_r is the reduced temperature, p_r is the reduced pressure, V_r is the reduced volume, and R is the universal gas constant.

Principle of corresponding states

Critical variables are useful for rewriting a varied equation of state into one that applies to all materials. The effect is similar to a normalizing constant. The principle of corresponding states indicates that substances at equal reduced pressures and temperatures have equal reduced volumes. This relationship is approximately true for many substances, but becomes increasingly inaccurate for large values of p_r

Table of liquid–vapor critical temperature and pressure for selected substances

Substance[3][4]	Critical temperature	Critical pressure
Argon	0150.8 !−122.4 °C (150.8 K)	0048.1 !48.1 atm (4,870 kPa)
Ammonia[5]	0405.6 !132.4 °C (405.6 K)	0111.3 !111.3 atm (11,280 kPa)
Bromine	0584.0 !310.8 °C (584.0 K)	0102 !102 atm (10,300 kPa)
Caesium	1938.00 !1,664.85 °C (1,938.00 K)	0094 !94 atm (9,500 kPa)
Chlorine	0417.0 !143.8 °C (417.0 K)	0076.0 !76.0 atm (7,700 kPa)
Ethanol	241 °C (514 K)	62.18 atm (63 bar, 6,300 kPa)
Fluorine	0144.30 !−128.85 °C (144.30 K)	0051.5 !51.5 atm (5,220 kPa)
Helium	0005.19 !−267.96 °C (5.19 K)	0002.24 !2.24 atm (227 kPa)
Hydrogen	0033.20 !−239.95 °C (33.20 K)	0012.8 !12.8 atm (1,300 kPa)
Krypton	0209.4 !−63.8 °C (209.4 K)	0054.3 !54.3 atm (5,500 kPa)
CH4	0044.40 !−82.3 °C (190.9 K)	0027.2 !45.79 atm (4,640 kPa)
Neon	0044.40 !−228.75 °C (44.40 K)	0027.2 !27.2 atm (2,760 kPa)
Nitrogen	0126.3 !−146.9 °C (126.3 K)	0033.5 !33.5 atm (3,390 kPa)
Oxygen	0154.6 !−118.6 °C (154.6 K)	0049.8 !49.8 atm (5,050 kPa)
CO2	0304.19 !31.04 °C (304.19 K)	0072.8 !72.8 atm (7,380 kPa)
N2O	0304.19 !36.4 °C (309.6 K)	0072.8 !71.5 atm (7,240 kPa)
H2SO4	0927 !654 °C (927 K)	0045.4 !45.4 atm (4,600 kPa)
Xenon	0289.8 !16.6 °C (289.8 K)	0057.6 !57.6 atm (5,840 kPa)
Lithium	3223 !2,950 °C (3,220 K)	0652 !652 atm (66,100 kPa)
Mercury	1750.1 !1,476.9 °C (1,750.1 K)	1720 !1,720 atm (174,000 kPa)
Sulfur	1314.00 !1,040.85 °C (1,314.00 K)	0207 !207 atm (21,000 kPa)
Iron	8500 !8,227 °C (8,500 K)
Gold	7250 !6,977 °C (7,250 K)	5000 !5,000 atm (510,000 kPa)
Aluminium	7850 !7,577 °C (7,850 K)
Water[6][7]	0647.096 !373.946 °C (647.096 K)	0217.7 !217.7 atm (22,060 kPa)

History

The existence of a critical point was first discovered by Thomas Andrews in 1869 for carbon dioxide. He showed that CO₂ could be liquefied at 31^oC at a pressure of 73 atm, but not at slightly higher temperatures even under very much higher pressures (to 3000 atm).

Mixtures: liquid–liquid critical point

A plot of typical polymer solution phase behavior including two critical points: an LCST and a UCST.

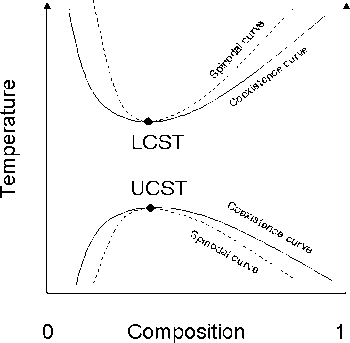
The liquid–liquid critical point of a solution denotes the limit of the two-phase region of the phase diagram. In other words, this is the point at which an infinitesimal change in some thermodynamic variable such as temperature or pressure will lead to separation of the mixture into two distinct liquid phases, as shown in the polymer–solvent phase diagram to the right. Such points may also be denoted a critical solution temperature. Two types of liquid–liquid critical points are the upper critical solution temperature, or UCST, which denotes the warmest point at which cooling will induce phase separation, and the lower critical solution temperature, which denotes the coolest point at which heating will induce phase separation.

Mathematical definition

From a theoretical standpoint, the liquid–liquid critical point represents the temperature-concentration extremum of the spinodal curve (this can be seen in the figure to the right). Thus in a two-component system it must satisfy two conditions. First is the condition of the spinodal curve, which is that the second derivative of the free energy with respect to concentration must equal zero. The second condition is the extremum condition that the third derivative of the free energy with respect to concentration must also equal zero, or that the derivative of the spinodal temperature with respect to concentration must equal zero.

In renormalization group theory

According to renormalization group theory, the defining property of criticality is that the natural length scale characteristic of the structure of the physical system, the so-called correlation length ξ, becomes infinite. This effect is the cause of the critical opalescence that is seen as the liquid–liquid critical point is approached in a binary fluid mixture. There are also lines in phase space along which this happens: these are critical lines.

In equilibrium systems the critical point is reached only by tuning a control parameter precisely. However, in some non-equilibrium systems the critical point is an attractor of the dynamics in a manner that is robust with respect to system parameters, a phenomenon referred to as self-organized criticality.

The critical point is described by a conformal field theory.

See also

• Conformal field theory
• Critical exponents
• Critical phenomena
• Joback method, Klincewicz method, Lydersen method (Estimation of critical temperature, pressure, and volume from molecular structure)
• Lower critical solution temperature
• Percolation thresholds
• Phase transition
• Rushbrooke inequality
• Scale invariance
• Self-organized criticality
• Supercritical fluid, Supercritical drying, Supercritical water oxidation
• Tricritical point
• Triple point
• Upper critical solution temperature
• Widom scaling

Footnotes

1. ^ International Association for the Properties of Water and Steam, 2007.
2. ^ Cengel, Yunus A.; Boles, Michael A. (2002). Thermodynamics: an engineering approach. Boston: McGraw-Hill. pp. 91–93. ISBN 0-07-121688-X. 
3. ^ Emsley, John (1991). The Elements ((Second Edition) ed.). Oxford University Press. ISBN 0-19-855818-X. 
4. ^ Thermodynamics: An Engineering Approach ((Fourth Edition) ed.). McGraw-Hill. 2002. pp. 824. ISBN 0-07-238332-1. 
5. ^ http://www.engineeringtoolbox.com/ammonia-d_971.html
6. ^ International Association for the Properties of Water and Steam, 2007.
7. ^ "Critical Temperature and Pressure". Purdue University. http://www.chem.purdue.edu/gchelp/liquids/critical.html. Retrieved 2006-12-19. 

References

• "Revised Release on the IAPWS Industrial Formulation 1997 for the Thermodynamic Properties of Water and Steam" (PDF). International Association for the Properties of Water and Steam. August 2007. http://www.iapws.org/relguide/IF97-Rev.pdf. Retrieved 2009-06-09. 

External links

• "Critical points for some common solvents". ProSciTech. Archived from the original on 2008-01-31. http://web.archive.org/web/20080131081956/http://www.proscitech.com.au/catalogue/notes/cpd.htm. 
• "Critical Temperature and Pressure". Department of Chemistry. Purdue University. http://www.chem.purdue.edu/gchelp/liquids/critical.html. Retrieved 2006-12-03. 
• Hagen Kleinert and Verena Schulte-Frohlinde, Critical Properties of φ⁴-Theories, World Scientific (Singapur, 2001); Paperback ISBN 981-02-4658-7 (readable online here)