VSEPR theory

Valence shell electron pair repulsion (VSEPR) theory is a model in chemistry used to predict the shape of individual molecules based upon the extent of electron-pair electrostatic repulsion.^[1] It is also named Gillespie–Nyholm theory after its two main developers. The acronym "VSEPR" is sometimes pronounced "vesper" for ease of pronunciation; however, the phonetic pronunciation is technically more correct.^[2]

The premise of VSEPR is that the valence electron pairs surrounding an atom mutually repel each other, and will therefore adopt an arrangement that minimizes this repulsion, thus determining the molecular geometry. The number of electron pairs surrounding an atom, both bonding and nonbonding, is called its steric number.

VSEPR theory is usually compared and contrasted with valence bond theory, which addresses molecular shape through orbitals that are energetically accessible for bonding. Valence bond theory concerns itself with the formation of sigma and pi bonds. Molecular orbital theory is another model for understanding how atoms and electrons are assembled into molecules and polyatomic ions.

VSEPR theory has long been criticized for not being quantitative, and therefore limited to the generation of "crude", even though structurally accurate, molecular geometries of covalent molecules. However, molecular mechanics force fields based on VSEPR have also been developed.^[3]

History

The idea of a correlation between molecular geometry and number of valence electrons (both shared and unshared) was first presented in a Bakerian Lecture in 1940 by Nevil Sidgwick and Herbert Powell at the University of Oxford.^[4] In 1957 Ronald Gillespie and Ronald Sydney Nyholm at University College London refined this concept to build a more detailed theory capable of choosing between various alternative geometries.^[5][6]

Description

VSEPR theory mainly involves predicting the layout of electron pairs surrounding one or more central atoms in a molecule, which are bonded to two or more other atoms. The geometry of these central atoms in turn determines the geometry of the larger whole.

The number of electron pairs in the valence shell of a central atom is determined by drawing the Lewis structure of the molecule, expanded to show all lone pairs of electrons, alongside protruding and projecting bonds. Where two or more resonance structures can depict a molecule, the VSEPR model is applicable to any such structure. For the purposes of VSEPR theory, the multiple electron pairs in a multiple bond are treated as though they were a single "pair".

These electron pairs are assumed to lie on the surface of a sphere centered on the central atom, and since they are negatively charged, tend to occupy positions that minimizes their mutual electrostatic repulsions by maximizing the distance between them. The number of electron pairs therefore determine the overall geometry that they will adopt.

For example, when there are two electron pairs surrounding the central atom, their mutual repulsion is minimal when they lie at opposite poles of the sphere. Therefore, the central atom is predicted to adopt a linear geometry. If there are 3 electron pairs surrounding the central atom, their repulsion is minimized by placing them at the vertices of an equilateral triangle centered on the atom. Therefore, the predicted geometry is trigonal. Similarly, for 4 electron pairs, the optimal arrangement is tetrahedral.

This overall geometry is further refined by distinguishing between bonding and nonbonding electron pairs. A bonding electron pair is involved in a sigma bond with an adjacent atom, and, being shared with that other atom, lies farther away from the central atom than does a nonbonding pair (lone pair), which is held close to the central atom by its positively-charged nucleus. Therefore, the repulsion caused by the lone pair is greater than the repulsion caused by the bonding pair. As such, when the overall geometry has two sets of positions that experience different degrees of repulsion, the lone pair(s) will tend to occupy the positions that experience less repulsion. In other words, the lone pair-lone pair (lp-lp) repulsion is considered to be stronger than the lone pair-bonding pair (lp-bp) repulsion, which in turn is stronger than the bonding pair-bonding pair (bp-bp) repulsion. Hence, the weaker bp-bp repulsion is preferred over the lp-lp or lp-bp repulsion.

This distinction becomes important when the overall geometry has two or more non-equivalent positions. For example, when there are 5 electron pairs surrounding the central atom, the optimal arrangement is a trigonal bipyramid. In this geometry, two positions lie at 180° angles to each other and 90° angles to the other 3 adjacent positions, whereas the other 3 positions lie at 120° to each other and at 90° to the first two positions. The first two positions therefore experience more repulsion than the last three positions. Hence, when there are one or more lone pairs, the lone pairs will tend to occupy the last three positions first.

The difference between lone pairs and bonding pairs may also be used to rationalize deviations from idealized geometries. For example, the H₂O molecule has four electron pairs in its valence shell: two lone pairs and two bond pairs. The four electron pairs are spread so as to point roughly towards the apices of a tetrahedron. However, the bond angle between the two O-H bonds is only 104.5°, rather than the 109.5° of a regular tetrahedron, because the two lone pairs (whose density or probability envelopes lie closer to the oxygen nucleus) exert a greater mutual repulsion than the two bond pairs.

AXE method

The "AXE method" of electron counting is commonly used when applying the VSEPR theory. The A represents the central atom and always has an implied subscript one. The X represents the number of sigma bonds between the central atoms and outside atoms. Multiple covalent bonds (double, triple, etc.) count as one X. The E represents the number of lone electron pairs surrounding the central atom. The sum of X and E, known as the steric number, is also associated with the total number of hybridized orbitals used by valence bond theory.

Based on the steric number and distribution of X's and E's, VSEPR theory makes the predictions in the following tables. Note that the geometries are named according to the atomic positions only and not the electron arrangement. For example the description of AX₂E₁ as bent means that AX₂ is a bent molecule without reference to the lone pair, although the lone pair helps to determine the geometry.

Steric No.	Basic geometry 0 lone pair	1 lone pair	2 lone pairs	3 lone pairs
2	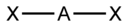Linear
3	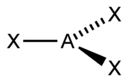Trigonal planar	Bent
4	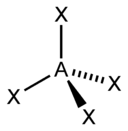Tetrahedral	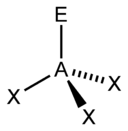Trigonal pyramid	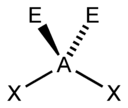Bent
5	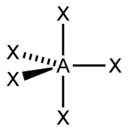Trigonal bipyramid	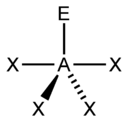Seesaw	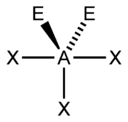T-shaped	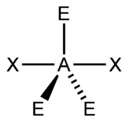Linear
6	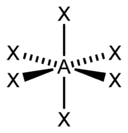Octahedral	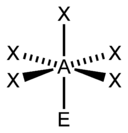Square pyramid	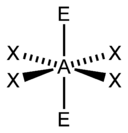Square planar
7	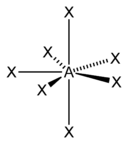Pentagonal bipyramid	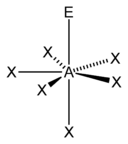Pentagonal pyramid
8	Square antiprismatic

Molecule Type	Shape	Electron arrangement†	Geometry‡	Examples
AX1En	Diatomic			HF, O2
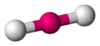
AX2E0	Linear			BeCl2, HgCl2, CO2
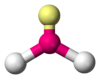
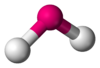
AX2E1	Bent			NO2−, SO2, O3
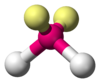
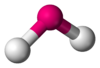
AX2E2	Bent			H2O, OF2
AX2E3	Linear	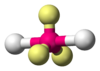		XeF2, I3−
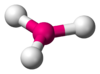
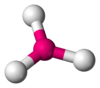
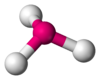
AX3E0	Trigonal planar			BF3, CO32−, NO3−, SO3
AX3E1	Trigonal pyramidal			NH3, PCl3
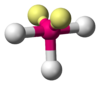
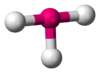
AX3E2	T-shaped			ClF3, BrF3
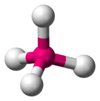
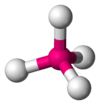
AX4E0	Tetrahedral			CH4, PO43−, SO42−, ClO4−
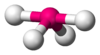
AX4E1	Seesaw			SF4
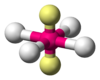
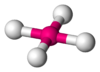
AX4E2	Square planar			XeF4
AX5E0	Trigonal bipyramidal	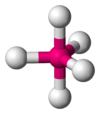		PCl5
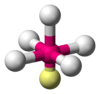
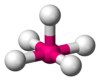
AX5E1	Square pyramidal			ClF5, BrF5
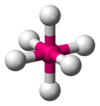
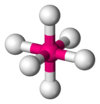
AX6E0	Octahedral			SF6
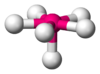
AX6E1	Pentagonal pyramidal			XeOF5−, IOF52− [7]
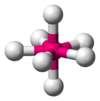
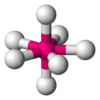
AX7E0	Pentagonal bipyramidal			IF7
AX8E0	Square antiprismatic			XeF2− 8

† Electron arrangement including lone pairs, shown in pale yellow ‡ Observed geometry (excluding lone pairs)

When the substituent (X) atoms are not all the same, the geometry is still approximately valid, but the bond angles may be slightly different from the ones where all the outside atoms are the same. For example, the double-bond carbons in alkenes like C₂H₄ are AX₃E₀, but the bond angles are not all exactly 120°. Similarly, SOCl₂ is AX₃E₁, but because the X substituents are not identical, the XAX angles are not all equal.

As a tool in predicting the geometry adopted with a given number of electron pairs, an often used physical demonstration of the principle of minimal electrostatic repulsion utilizes inflated balloons. Through handling, balloons acquire a slight surface electrostatic charge that results in the adoption of roughly the same geometries when they are tied together at their stems as the corresponding number of electron pairs. For example, five balloons tied together adopt the trigonal bipyramidal geometry just as do the five bonding pairs of a PCl₅ molecule (AX₅) or the two bonding and three non-boning pairs of a XeF₂ molecule (AX₂E₃). The molecular geometry of the former is also trigonal bipyramidal, while that of the latter is linear.

Examples

The methane molecule (CH₄) is tetrahedral because there are four pairs of electrons. The four hydrogen atoms are positioned at the vertices of a tetrahedron, and the bond angle is cos⁻¹(-1/3) ≈ 109°28'. This is referred to as an AX₄ type of molecule. As mentioned above, A represents the central atom and X represents all of the outer atoms.

The ammonia molecule (NH₃) has three pairs of electrons involved in bonding, but there is a lone pair of electrons on the nitrogen atom. It is not bonded with another atom; however, it influences the overall shape through repulsions. As in methane above, there are four regions of electron density. Therefore, the overall orientation of the regions of electron density is tetrahedral. On the other hand, there are only three outer atoms. This is referred to as an AX₃E type molecule because the lone pair is represented by an E. The observed shape of the molecule is a trigonal pyramid, because the lone pair is not "visible" in experimental methods used to determine molecular geometry. The shape of a molecule is found from the relationship of the atoms even though it can be influenced by lone pairs of electrons.

A steric number of seven is possible, but it occurs in uncommon compounds such as iodine heptafluoride (IF₇) . The base geometry for this is pentagonal bipyramidal.

The most common geometry for a steric number of eight is a square antiprismatic geometry.^[8] Examples of this include the octafluoroxenate ion (XeF2−
8) in nitrosonium octafluoroxenate(VI),^[9][10] octacyanomolybdate (Mo(CN)4−
8), and octafluorozirconate (ZrF4−
8).^[8]

Exceptions

There are groups of compounds where VSEPR fails to predict the correct geometry.

Transition metal compounds

Many transition metal compounds do not have geometries explained by VSEPR which can be ascribed to there being no lone pairs in the valence shell and the interaction of core d electrons with the ligands.^[11] The structure of some of these compounds, including metal hydrides and alkyl complexes such as hexamethyltungsten, can be predicted correctly using the VALBOND theory, which is based on sd hybrid orbitals and the 3-center-4-electron bonding model.^[12][13] Crystal field theory is another theory that can often predict the geometry of coordination complexes.

Group 2 halides

The gas phase structures of the triatomic halides of the heavier members of group 2, (i.e. calcium, strontium and barium halides, MX₂), are not linear as predicted but are bent, (approximate X-M-X angles: CaF₂, 145°; SrF₂, 120°; BaF₂, 108°; SrCl₂, 130°; BaCl₂, 115°; BaBr₂, 115°; BaI₂, 105°).^[14] It has been proposed by Gillespie that this is caused by interaction of the ligands with the electron core of the metal atom, polarising it so that the inner shell is not spherically symmetric, thus influencing the molecular geometry.^[11][15]

Some AX₂E₂ molecules

One example is molecular lithium oxide, Li₂O, which is linear rather than being bent, and this has been ascribed to the bonding being essentially ionic leading to strong repulsion between the lithium atoms.^[16]
Another example is O(SiH₃)₂ with an Si-O-Si angle of 144.1° which compares to the angles in Cl₂O (110.9°), (CH₃)₂O (111.7°)and N(CH₃)₃ (110.9°). Gillespie's rationalisation is that the localisation of the lone pairs, and therefore their ability to repel other electron pairs, is greatest when the ligand has an electronegativity similar to, or greater than, the central atom.^[11] When the central atom is more electronegative, as in O(SiH₃)₂, the lone pairs are less well localised, have a weaker repulsive effect and this combined with the stronger ligand-ligand repulsion (-SiH₃ is a relatively large ligand compared to the examples above) gives the larger than expected Si-O-Si bond angle.^[11]

Some AX₆E₁molecules

Some AX₆E₁ molecules, e.g. the Te(IV) and Bi(III) anions, TeCl₆²⁻, TeBr₆²⁻, BiCl₆³⁻, BiBr₆³⁻ and BiI₆³⁻, are regular octahedra and the lone pair does not affect the geometry.^[17] One rationalization is that steric crowding of the ligands allows no room for the non-bonding lone pair;^[11] another rationalization is the inert pair effect.^[18]

VSEPR and localized orbitals

The VSEPR theory places each pair of valence electrons in a bond or a lone pair found in a local region of the molecule. Molecular orbital theory yields a set of orbitals which have the symmetry of the molecule and which are delocalized over several atoms. However these orbitals can be transformed into an equivalent set of localized molecular orbitals.

In the water molecule for example, molecular orbital calculations yield two lone pairs, one an s-p hybrid in the plane of the molecule and one a pure p orbital perpendicular to this plane. These orbitals can be combined into two sp³ nonbonding orbitals, equivalent to each other, which can be compared to the lone pairs of VSEPR theory. Similarly there are two calculated bonding orbitals each extending over all three atoms, which can be combined into two localized orbitals, one for each bond.

The delocalized and localized orbitals provide completely equivalent descriptions of the ground state, since the total wavefunction for all electrons is a Slater determinant which is unchanged by the transformation of the orbitals.^[19]

See also

• Bent's rule (effect of ligand electronegativity)
• Linear combination of atomic orbitals
• Molecular geometry
• Molecular modelling
• Software for molecular modeling
• Valency interaction formula

References

1. ^ Jolly, W. L.,Modern Inorganic Chemistry, McGraw-Hill, 1984 ISBN 0-07-032760-2
2. ^ H. Stephen Stoker (2009). General, Organic, and Biological Chemistry. Cengage Learning. p. 119. ISBN 0547152817, 9780547152813. 
3. ^ Box, Vernon G. S. (1997-03-17). "The Molecular Mechanics of Quantized Valence Bonds". Journal of Molecular Modeling 3 (3): 124–141. doi:10.1007/s008940050026. http://www.springerlink.com/content/gkflr3c9jm4n9qwc/. Retrieved 28 September 2011. 
4. ^ http://www.jstor.org/pss/97507 N.V.Sidgwick and H.M.Powell, Proc.Roy.Soc.A 176, 153–180 (1940) Bakerian Lecture. Stereochemical Types and Valency Groups
5. ^ R.J.Gillespie and R.S.Nyholm, Quart.Rev. 11, 339 (1957)
6. ^ R.J.Gillespie, J.Chem.Educ. 47, 18(1970)
7. ^ Baran, E. (2000). "Mean amplitudes of vibration of the pentagonal pyramidal XeOF₅⁻ and IOF₅²⁻ anions". Journal of Fluorine Chemistry 101: 61–63. doi:10.1016/S0022-1139(99)00194-3.  edit
8. ^ ^{a b} Wiberg, Egon (2001). Inorganic Chemistry. Arnold Frederick Holleman. Academic Press. p. 1165. ISBN 0123526515. 
9. ^ Peterson, W. .; Holloway, H. .; Coyle, A. .; Williams, M. . (Sep 1971). "Antiprismatic Coordination about Xenon: the Structure of Nitrosonium Octafluoroxenate(VI)". Science 173 (4003): 1238–1239. Bibcode 1971Sci...173.1238P. doi:10.1126/science.173.4003.1238. ISSN 0036-8075. PMID 17775218.  edit
10. ^ Hanson, Robert M. (1995). Molecular origami: precision scale models from paper. University Science Books. ISBN 093570230X. 
11. ^ ^{a b c d e} Models of molecular geometry, Gillespie R. J., Robinson E.A. Chem. Soc. Rev., 2005, 34, 396–407, doi: 10.1039/b405359c
12. ^ Landis, C. K.; Cleveland, T.; Firman, T. K. Making sense of the shapes of simple metal hydrides. J. Am. Chem. Soc. 1995, 117, 1859–1860.
13. ^ Landis, C. K.; Cleveland, T.; Firman, T. K. Structure of W(CH₃)₆. Science 1996, 272, 182–183.
14. ^ Greenwood, Norman N.; Earnshaw, Alan (1997). Chemistry of the Elements (2nd ed.). Oxford: Butterworth-Heinemann. ISBN 0080379419. 
15. ^ Core Distortions and Geometries of the Difluorides and Dihydrides of Ca, Sr, and Ba Bytheway I, Gillespie R.J, Tang T.H., Bader R.F. Inorganic Chemistry, 34,9, 2407–2414, 1995 doi:10.1021/ic00113a023
16. ^ A spectroscopic determination of the bond length of the LiOLi molecule: Strong ionic bonding, D. Bellert, W. H. Breckenridge, J. Chem. Phys. 114, 2871 (2001); doi:10.1063/1.1349424
17. ^ Wells A.F. (1984) Structural Inorganic Chemistry 5th edition Oxford Science Publications ISBN 0-19-855370-6
18. ^ Housecroft, C. E.; Sharpe, A. G. (2004). Inorganic Chemistry (2nd ed.). Prentice Hall. ISBN 978-0130399137. 
19. ^ Levine I.N., “Quantum Chemistry” (4th ed., Prentice-Hall 1991) sec.15.8

Further reading

• Chemistry: Foundations and Applications. J. J. Lagowski, ed. New York: Macmillan, 2004. ISBN 0028657217. Volume 3, pages 99–104.

External links

• 3D Chem - Chemistry, Structures, and 3D Molecules
• IUMSC - Indiana University Molecular Structure Center