Molecular orbital

See also: Molecular orbital theory

In chemistry, a molecular orbital (or MO) is a mathematical function describing the wave-like behavior of an electron in a molecule. This function can be used to calculate chemical and physical properties such as the probability of finding an electron in any specific region. The term "orbital" was first used in English by Robert S. Mulliken as the English translation of Schrödinger's 'Eigenfunktion'. It has since been equated with the "region" generated with the function. Molecular orbitals are usually constructed by combining atomic orbitals or hybrid orbitals from each atom of the molecule, or other molecular orbitals from groups of atoms. They can be quantitatively calculated using the Hartree-Fock or Self-Consistent Field (SCF) methods.

Figure 1: Complete acetylene (H–C≡C–H) molecular orbital set

Overview

Molecular orbitals (MOs) represent regions in a molecule where an electron is likely to be found. Molecular orbitals are obtained from the combination of atomic orbitals, which predict the location of an electron in an atom. A molecular orbital can specify the electron configuration of a molecule: the spatial distribution and energy of one (or one pair of) electron(s). Most commonly an MO is represented as a linear combination of atomic orbitals (the LCAO-MO method), especially in qualitative or very approximate usage. They are invaluable in providing a simple model of bonding in molecules, understood through molecular orbital theory. Most present-day methods in computational chemistry begin by calculating the MOs of the system. A molecular orbital describes the behavior of one electron in the electric field generated by the nuclei and some average distribution of the other electrons. In the case of two electrons occupying the same orbital, the Pauli principle demands that they have opposite spin. Necessarily this is an approximation, and highly accurate descriptions of the molecular electronic wave function do not have orbitals (see configuration interaction).

Formation of Molecular Orbitals

Molecular orbitals arise from allowed interactions between atomic orbitals, which are allowed if the symmetries (determined from group theory) of the atomic orbitals are compatible with each other. Efficiency of atomic orbital interactions is determined from the overlap (a measure of how well two orbitals constructively interact with one another) between two atomic orbitals, which is significant if the atomic orbitals are close in energy. Finally, the number of molecular orbitals that form must equal the number of atomic orbitals in the atoms being combined to form the molecule.

Qualitative discussion

For an imprecise, but qualitatively useful, discussion of the molecular structure, the molecular orbitals can be obtained from the "Linear combination of atomic orbitals molecular orbital method" ansatz. Here, the molecular orbitals are expressed as linear combinations of atomic orbitals.

Linear combinations of atomic orbitals (LCAO)

Molecular orbitals were first introduced by Friedrich Hund^[1][2] and Robert S. Mulliken^[3][4] in 1927 and 1928.^[5][6] The linear combination of atomic orbitals or "LCAO" approximation for molecular orbitals was introduced in 1929 by Sir John Lennard-Jones.^[7]. His ground-breaking paper showed how to derive the electronic structure of the fluorine and oxygen molecules from quantum principles. This qualitative approach to molecular orbital theory is part of the start of modern quantum chemistry. Linear combinations of atomic orbitals (LCAO) can be used to estimate the molecular orbitals that are formed upon bonding between the molecule’s constituent atoms. Similar to an atomic orbital, a Schrodinger equation, which describes the behavior of an electron, can be constructed for a molecular orbital as well. Linear combinations of atomic orbitals, or the sums and differences of the atomic wavefunctions, provide approximate solutions to the molecular Schrodinger equations. For simple diatomic molecules, the obtained wavefunctions are represented mathematically by the equations

Ψ = c_aψ_a + c_bψ_b

Ψ ^* = c_aψ_a − c_bψ_b

where Ψ and Ψ ^* are the molecular wavefunctions for the bonding and antibonding molecular orbitals, respectively, ψ_a and ψ_b are the atomic wavefunctions from atoms a and b, respectively, and c_a and c_b are adjustable coefficients. These coefficients can be positive or negative, depending on the energies and symmetries of the individual atomic orbitals. As the two atoms become closer together, their atomic orbitals overlap to produce areas of high electron density, and, as a consequence, molecular orbitals are formed between the two atoms. The atoms are held together by the electrostatic attraction between the positively charged nuclei and the negatively charged electrons occupying bonding molecular orbitals.^[8]

Bonding, Antibonding, and Nonbonding MOs

When atomic orbitals interact, the resulting molecular orbital can be of three types: bonding, antibonding, or nonbonding.

Bonding MOs:

• Bonding interactions between atomic orbitals are constructive (in-phase) interactions.
• Bonding MOs are lower in energy than the atomic orbitals that combine to produce them.

Antibonding MOs:

• Antibonding interactions between atomic orbitals are destructive (out-of-phase) interactions.
• Antibonding MOs are higher in energy than the atomic orbitals that combine to produce them.

Nonbonding MOs:

• Nonbonding MOs are the result of no interaction between atomic orbitals because of lack of compatible symmetries.
• Nonbonding MOs will have the same energy as the atomic orbitals of one of the atoms in the molecule.

Sigma and Pi Labels for MOs

The type of interaction between atomic orbitals can be further categorized by the symmetry labels: σ (sigma) and π (pi).

σ-symmetry

A MO with σ-symmetry results from the interaction of either two atomic s-orbitals or two atomic p_z-orbitals. A MO will have σ-symmetry if the orbital is symmetrical with respect to the axis joining the two nuclear centers, the internuclear axis. This means that rotation of the MO about the internuclear axis does not result in a phase change. A σ*-orbital, sigma antibonding orbital, also maintains the same phase when rotated about the internuclear axis. The σ*-orbital has a nodal plane that is between the nuclei and perpendicular to the internuclear axis.^[9]

π -symmetry

A MO with π –symmetry results from the interaction of either two atomic p_x-orbitals or p_y-orbitals. A MO will have π-symmetry if the orbital is asymmetrical with respect to rotation about the internuclear axis. This means that rotation of the MO about the internuclear axis will result in a phase change. A π*-orbital, pi antibonding orbital, will also produce a phase change when rotated about the internuclear axis. The π *-orbital also has a nodal plane between the nuclei.^{[10][11][12][13]}

Gerade and ungerade symmetry

For molecules that possess a center of inversion (centrosymmetric molecules) there are additional labels of symmetry that can be applied to molecular orbitals. Centrosymmetric molecules include:

• Homonuclear, X₂
• Octahedral, EX₆
• Square planar, EX₄.

Non-centrosymmetric molecules include:

• Heteronuclear, XY
• Tetrahedral, EX₄.

If inversion through the center of symmetry in a molecule results in the same phases for the molecular orbital, then the MO is said to have gerade, g, symmetry. If inversion through the center of symmetry in a molecule results in a phase change for the molecular orbital, then the MO is said to have ungerade, u, symmetry. For a bonding MO with σ-symmetry, the orbital can be labeled σ_g, and for an antibonding MO with σ-symmetry the orbital can be labeled σ_u, because inversion through the center of symmetry for Figure 4(b) would produce a sign change. For a bonding MO with π -symmetry the orbital can be labeled π_u because inversion through the center of symmetry for Figure 5(c) would produce a sign change. However, for an antibonding MO with π -symmetry the orbital can be labeled π_g because inversion through the center of symmetry for Figure 5(d) would not produce a sign change.^[14]

MO diagrams

Main article: Molecular orbital diagram

The qualitative approach of MO uses a molecular orbital diagram to visualize bonding interactions in a molecule. In this type of diagram, the molecular orbitals are represented by horizontal lines; the higher a line the higher the energy of the orbital, and degenerate orbitals are placed on the same level with a space between them. Then, the electrons to be placed in the molecular orbitals are slotted in one by one, keeping in mind the Pauli exclusion principle and Hund's rule of maximum multiplicity (only 2 electrons, having opposite spins, per orbital; place as many unpaired electrons on one energy level as possible before starting to pair them). For more complicated molecules, the wave mechanics approach loses utility in a qualitative understanding of bonding (although is still necessary for a quantitative approach). Some properties:

• A basis set of orbitals includes those atomic orbitals that are available for molecular orbital interactions, which may be bonding or antibonding
• The number of molecular orbitals is equal to the number of atomic orbitals included in the linear expansion or the basis set
• If the molecule has some symmetry, the degenerate atomic orbitals (with the same atomic energy) are grouped in linear combinations (called symmetry-adapted atomic orbitals (SO)), which belong to the representation of the symmetry group, so the wave functions that describe the group are known as symmetry-adapted linear combinations (SALC).
• The number of molecular orbitals belonging to one group representation is equal to the number of symmetry-adapted atomic orbitals belonging to this representation
• Within a particular representation, the symmetry-adapted atomic orbitals mix more if their atomic energy levels are closer.

Bonding in molecular orbitals

Orbital degeneracy

Main article: Degenerate orbital

Molecular orbitals are said to be degenerate if they have the same energy. For example, in the homonuclear diatomic molecules of the first ten elements, the molecular orbitals derived from the p_x and the p_y atomic orbitals result in two degenerate bonding orbitals (of low energy) and two degenerate antibonding orbitals (of high energy). ^[15]

Ionic bonds

Main article: Ionic bond

When the energy difference between the atomic orbitals of two atoms is quite large, one atom's orbitals contribute almost entirely to the bonding orbitals, and the others atom’s orbitals contribute almost entirely to the antibonding orbitals. Thus, the situation is effectively that some electrons have been transferred from one atom to the other. This is called an (mostly) ionic bond.

Bond order and length

Main article: Bond length

The bond order, or number of bonds, of a molecule can be determined by combining the number of electrons in bonding and antibonding molecular orbitals as follows:

Bond order = 0.5*[(number of electrons in bonding orbitals) - (number of electrons in antibonding orbitals)]

For example, N₂, with eight electrons in bonding orbitals and two electrons in antibonding orbitals, has a bond order of three, which constitutes a triple bond. Bond length is inversely proportional to bond order. Data illustrating this principle for diatomic species of elements in the second row of the periodic table are shown in Figure 6.

Note that although Be₂ has a bond order of 0 according to MO, there is experimental evidence of a highly unstable Be₂ compound having a bond length of 245 pm and bond energy of 10kJ/mol. .^[16]

HOMO and LUMO

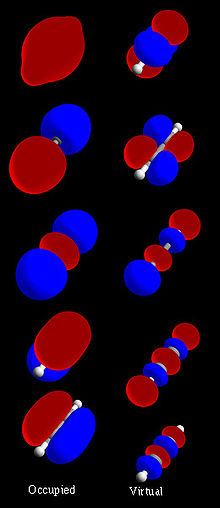
Main article: HOMO/LUMO

The highest occupied molecular orbital and lowest unoccupied molecular orbital are often referred to as the HOMO and LUMO, respectively. The difference of the energies of the HOMO and LUMO, termed the band gap, can sometimes serve as a measure of the excitability of the molecule: The smaller the energy the more easily it will be excited. (more information forthcoming)

Molecular Orbital Examples

Homonuclear diatomics

Homonuclear diatomic MOs contain equal contributions from each atomic orbital in the basis set. This is shown in the homonuclear diatomic MO diagrams for H₂, He₂, and Li₂, all of which containing symmetric orbitals. ^[17]

H₂

As a simple MO example consider the hydrogen molecule, H₂ (see molecular orbital diagram), with the two atoms labelled H' and H". The lowest-energy atomic orbitals, 1s' and 1s", do not transform according to the symmetries of the molecule. However, the following symmetry adapted atomic orbitals do:

1s' - 1s"	Antisymmetric combination: negated by reflection, unchanged by other operations
1s' + 1s"	Symmetric combination: unchanged by all symmetry operations

The symmetric combination (called a bonding orbital) is lower in energy than the basis orbitals, and the antisymmetric combination (called an antibonding orbital) is higher. Because the H₂ molecule has two electrons, they can both go in the bonding orbital, making the system lower in energy (and, hence, more stable) than two free hydrogen atoms. This is called a covalent bond. The bond order is equal to the number of bonding electrons minus the number of antibonding electrons, divided by 2. In this example, there are 2 electrons in the bonding orbital and none in the antibonding orbital; the bond order is 1, and there is a single bond between the two hydrogen atoms.

Figure 9: Electron wavefunctions for the 1s orbital of the hydrogen atom (left and right) and the corresponding bonding (bottom) and antibonding (top) molecular orbitals of the H₂ molecule. The real part of the wavefunction is the blue curve, and the imaginary part is the red curve. The red dots mark the locations of the protons. The electron wavefunction oscillates according to the Schrödinger wave equation, and orbitals are its standing waves. The standing wave frequency is proportional to the orbital's energy. (This plot is a one-dimensional slice through the three-dimensional system.)

He₂

On the other hand, consider the hypothetical molecule of He₂ (see molecular orbital diagram) with the atoms labeled He' and He". Again, the lowest-energy atomic orbitals, 1s' and 1s", do not transform according to the symmetries of the molecule, while the following symmetry adapted atomic orbitals do:

1s' - 1s"	Antisymmetric combination: negated by reflection, unchanged by other operations
1s' + 1s"	Symmetric combination: unchanged by all symmetry operations

Similar to the molecule H₂, the symmetric combination (called a bonding orbital) is lower in energy than the basis orbitals, and the antisymmetric combination (called an antibonding orbital) is higher. However, in its neutral ground state, each helium atom contains two electrons in its 1s orbital, combining for a total of four electrons. Two electrons fill the lower-energy bonding orbital, while the remaining two fill the higher-energy antibonding orbital. Thus, the resulting electron density around the molecule does not support the formation of a bond between the two atoms (called a sigma bond); therefore, the molecule does not exist. Another way of looking at it is that there are two bonding electrons and two antibonding electrons; therefore, the bond order is 0 and no bond exists. This is shown in Figure 10(a) in which two electrons occupy the σ_g(1s) bonding orbital and two electrons occupy the σ_u*(1s) antibonding orbital.

Li₂

Dilithium Li₂ is formed from the overlap of the 1s and 2s atomic orbitals (the basis set) of two Li atoms. Each Li atom contributes three electrons for bonding interactions, and the six electrons fill the three MOs of lowest energy, σ_g(1s), σ_u*(1s), and σ_g(2s) in the MO diagram in Figure 10(b). Using the equation for bond order, it is found that dilithium has a bond order of one, a single bond.

Noble gases

Considering a hypothetical molecule of He₂, since the basis set of atomic orbitals is the same as in the case of H₂, we find that both the bonding and antibonding orbitals are filled, so there is no energy advantage to the pair. HeH would have a slight energy advantage, but not as much as H₂ + 2 He, so the molecule exists only a short while. In general, we find that atoms such as He that have completely full energy shells rarely bond with other atoms. Except for short-lived Van der Waals complexes, there are very few noble gas compounds known.

Heteronuclear diatomics

While MOs for homonuclear diatomic molecules contain equal contributions from each interacting atomic orbital, MOs for heteronuclear diatomics contain different atomic orbital contributions. Orbital interactions to produce bonding or antibonding orbitals in heteronuclear diatomics occur if there is sufficient overlap between atomic orbitals as determined by their symmetries and similarity in orbital energies.

HF

In hydrogen fluoride HF overlap between the H 1s and F 2s orbitals is allowed by symmetry but the difference in energy between the two atomic orbitals prevents them from interacting to create a molecular orbital. Overlap between the H 1s and F 2p_z orbitals is also symmetry allowed, and these two atomic orbitals have a small energy separation. Thus, they interact, leading to creation of σ and σ* MOs and a molecule with a bond order of 1. Since HF is a non-centrosymmetric molecule, the symmetry labels g and u do not apply to its molecular orbitals.^[18]

Quantitative approach

To obtain quantitative values for the molecular energy levels, one needs to have molecular orbitals that are such that the configuration interaction (CI) expansion converges fast towards the full CI limit. The most common method to obtain such functions is the Hartree–Fock method, which expresses the molecular orbitals as eigenfunctions of the Fock operator. One usually solves this problem by expanding the molecular orbitals as linear combinations of Gaussian functions centered on the atomic nuclei (see linear combination of atomic orbitals and basis set (chemistry)). The equation for the coefficients of these linear combinations is a generalized eigenvalue equation known as the Roothaan equations, which are in fact a particular representation of the Hartree-Fock equation. There are a number of programs in which quantum chemical calculations of MOs can be performed, including Spartan and HyperChem.

Simple accounts often suggest that experimental molecular orbital energies can be obtained by the methods of ultra-violet photoelectron spectroscopy for valence orbitals and X-ray photoelectron spectroscopy for core orbitals. This, however, is incorrect as these experiments measure the ionization energy, the difference in energy between the molecule and one of the ions resulting from the removal of one electron. Ionization energies are linked approximately to orbital energies by Koopmans' theorem. While the agreement between these two values can be close for some molecules, it can be very poor in other cases.

References

1. ^ F. Hund, "Zur Deutung einiger Erscheinungen in den Molekelspektren" [On the interpretation of some phenomena in molecular spectra] Zeitschrift für Physik, vol. 36, pages 657-674 (1926).
2. ^ F. Hund, "Zur Deutung der Molekelspektren," Zeitschrift für Physik, Part I, vol. 40, pages 742-764 (1927); Part II, vol. 42, pages 93-120 (1927); Part III, vol. 43, pages 805-826 (1927); Part IV, vol. 51, pages 759-795 (1928); Part V, vol. 63, pages 719-751 (1930).
3. ^ R. S. Mulliken, "Electronic states. IV. Hund's theory; second positive nitrogen and Swan bands; alternate intensities," Physical Review, vol. 29, pages 637 - 649 (1927).
4. ^ R. S. Mulliken, "The assignment of quantum numbers for electrons in molecules," Physical Review, vol. 32, pages 186 - 222 (1928).
5. ^ Friedrich Hund and Chemistry, Werner Kutzelnigg, on the occasion of Hund's 100th birthday, Angewandte Chemie International Edition, 35, 573 - 586, (1996)
6. ^ Robert S. Mulliken's Nobel Lecture, Science, 157, no. 3785, 13 - 24, (1967). Available on-line at: Nobelprize.org .
7. ^ Sir John Lennard-Jones, "The electronic structure of some diatomic molecules," Transactions of the Faraday Society, vol. 25, pages 668-686 (1929).
8. ^ Gary L. Miessler; Donald A. Tarr. Inorganic Chemistry. Pearson Prentice Hall, 3rd ed., 2004.
9. ^ Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, p. 29-33.
10. ^ Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, p. 29-33.
11. ^ Peter Atkins; Julio De Paula. Atkins’ Physical Chemistry. Oxford University Press, 8th ed., 2006.
12. ^ Yves Jean; Francois Volatron. An Introduction to Molecular Orbitals. Oxford University Press, 1993.
13. ^ Michael Munowitz, Principles of Chemistry, Norton & Company, 2000, p. 229-233.
14. ^ Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, p. 29-33.
15. ^ Gary L. Miessler; Donald A. Tarr. Inorganic Chemistry. Pearson Prentice Hall, 3rd ed., 2004.
16. ^ Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, p. 29-33.
17. ^ Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, p. 29-33.
18. ^ Catherine E. Housecroft, Alan G, Sharpe, Inorganic Chemistry, Pearson Prentice Hall; 2nd Edition, 2005, p. 41-43.

External links

• Java molecular orbital viewer shows orbitals of hydrogen molecular ion.
• The orbitron, a visualization of all atomic, and some molecular and hybrid orbitals
• xeo Visualizations of some atomic and molecular atoms
• Simulations of molecules with electrons caught in molecular orbital (Simulations run on PC only.)